Латыпова АД_Э-289Б_СРС2. Отчет по самостоятельной работе 2 по дисциплине
 Скачать 39.11 Kb. Скачать 39.11 Kb.
|
|
ФГБОУ ВО Уфимский государственный авиационный технический университет Кафедра экономики предпринимательства ОТЧЕТпо самостоятельной работе № 2 по дисциплинеСтатистика Выполнил: Студент группы Э-289Б Латыпова Айгуль Данисовна Вариант 6 Проверил: д-р техн наук, профессор Е. В. Орлова Уфа- 2021 Задача 1. Средний квадрат отклонений вариантов признака от произвольной величины равен а. Средняя величина признака больше произвольной величины на 6 и равна 10. Найти коэффициент вариации. a = 66 Решение: (x - xp)2 =66 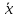 = 10 = 10( 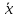 - xp) = 6 - xp) = 6Найдём дисперсию по формуле: 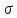 2 = 2 =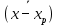 2 - ( 2 - ( 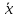 -xp) =66 -62 =30 -xp) =66 -62 =30От сюда,среднеквадратическое отклонение будет равно квадратному корню из дисперсии 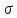 = =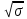 =5,47 =5,47Найдём коэффициент вариации: V = 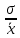 * 100% = * 100% = 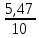 * 100 = 54,7 * 100 = 54,7Задача 2. Имеются статистические данные о выпуске продукции по десяти предприятиям отрасли. Для показателя выпуска продукции определить: моду, медиану, размах вариации, среднее линейное отклонение, дисперсию, среднее квадратическое отклонение. Рассчитать относительные показатели вариации. Рассчитать показатели асимметрии и эксцесса. Сделать вывод об однородности статистической совокупности.
Решение: Мода - это величина признака,которая наиболее часто встречается в совокупности. В данной задаче все выпуски продукции индивидуальны, и нельзя сказать какая из них встречается наиболее часто. Поэтому мода в данном ряду распределения отсутствует. Для нахождения медианы варианты этого ряда ранжируем все значения по возрастанию: 1,35 1,71 2,07 2,25 2,25 2,52 2,88 3,15 7,74 8,46 Выберем вариант, стоящий в середине полученного ряда: Me = 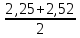 = 2,385 млн. руб. = 2,385 млн. руб.Размах вариации определяется как разность между наибольшим и наименьшим значением признака: R = xmax -xmin =8,46 -1,35=7,11 млн. руб. Среднее линейное отклонение вычисляется как средняя арифметическая из абсолютных значений отклонений вариант хi от среднего значения 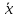 = = 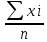 = = 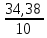 =3,438 =3,438
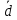 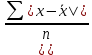 = = 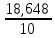 = 1,8648 = 1,8648Варианты выпуска продукции отклоняются от их средней величины в среднем на 1,8648 млн. руб. Дисперсия: 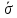 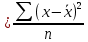 = = 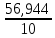 = 5,6994 млн. руб. = 5,6994 млн. руб.Среднеквадратическое отклонение: 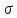 = =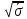 =2,387 млн. руб. =2,387 млн. руб.Рассчитаем относительные показатели вариации: Коэффициент осцилляции: VR = 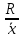 * 100% = * 100% = 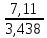 * 100% =206,8 % * 100% =206,8 %Коэффициент вариации: V 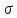 = = 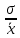 * 100% = * 100% =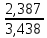 * 100% =69,43% * 100% =69,43%Поскольку V > 33% , следовательно совокупность неоднородна. Рассчитаем показатель асимметрии через отношение центрального момента третьего порядка к среднему квадратическому отклонению данного ряда в кубе: Где 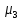 = = 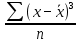 = = 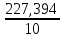 = 22,274 = 22,274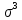 =( 2,387)3= 13,6 =( 2,387)3= 13,6As = 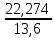 = 1,638 = 1,638Так как величина показателя асимметрии положительна, следовательно, речь идёт о правосторонней асимметрии. Задача 3. По данным о производстве продукции в двух подразделениях (бригадах) оценить внутригрупповые дисперсии, среднюю из внутригрупповых дисперсий, межгрупповую дисперсию, общую дисперсию, эмпирическое корреляционное соотношение. Оценить связь между группировочным и результативным признаками. Сделать содержательные выводы.
Решение: Рассчитаем внутригрупповые дисперсии:
Среднее производство продукции в бригаде №1: 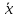 1 = 1 = 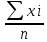 = = 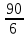 = 15 = 15Среднее производство продукции в бригаде №2: 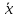 2 = 2 = 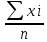 = = 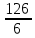 =21 =21Среднее производство продукции в бригаде №3: 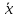 3 = 3 = 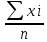 = = 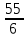 = 9,16 = 9,16Внутригрупповая дисперсия бригады №1: 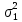 = = 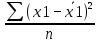 = = 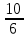 =1,6 =1,6Внутригрупповая дисперсия бригады №2 : 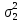 = = 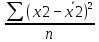 = = 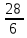 =4,667 =4,667Внутригрупповая дисперсия бригады №3: 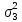 = = 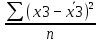 = = 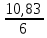 =1,805 =1,805Средняя из внутригрупповых дисперсий 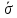 2 = 2 = 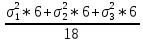 = 2,7 = 2,7Расчёт межгрупповой дисперсии: 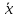 0= 0= 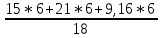 = 15,05 = 15,05
Межгрупповая дисперсия : 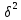 = =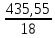 = 24,197 = 24,197Расчёт общей дисперсии : 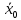 = = 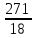 =15,05 =15,05
Общая дисперсия : 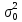 = = 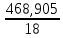 = 26,05 = 26,05Эмпирический коэффициент детерминации : 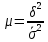 = = 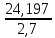 =8,962 или 89,62% =8,962 или 89,62%Эмпирическое корреляционное отношение : 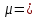 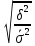 = 2,994 = 2,994Вывод: 89,62% производительности рабочих обусловлены принадлежности к бригаде №1,№2 и №3 и 10,38%- влиянием других факторов | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||