Отчет по выполнению лабораторных работ по дисциплине физическая и коллоидная химия
 Скачать 5.83 Mb. Скачать 5.83 Mb.
|
|
Обработка результатов измерений Уравнение (9.2), которое описывает скорость набухания полимера, является линейным в координатах( 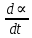 , α) . Во-первых, надо проверить, укладываются ли экспериментальные данные на прямую линию в указанных координатах. В случае выполнения линейной зависимости , α) . Во-первых, надо проверить, укладываются ли экспериментальные данные на прямую линию в указанных координатах. В случае выполнения линейной зависимости 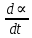 от можно определить кинетические параметры процесса набухания: от можно определить кинетические параметры процесса набухания: 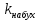 и и 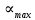 , а затем решить обратную задачу, т.е. рассчитать по уравнению (9.3) теоретическую кривую , а затем решить обратную задачу, т.е. рассчитать по уравнению (9.3) теоретическую кривую 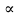 =f(t) и сопоставить ее с экспериментальными данными. С этой целью необходимо выполнить следующее: По данным таблицы 9.1 построить кривую зависимости степени набухания от времени (рисунок 9.2). =f(t) и сопоставить ее с экспериментальными данными. С этой целью необходимо выполнить следующее: По данным таблицы 9.1 построить кривую зависимости степени набухания от времени (рисунок 9.2).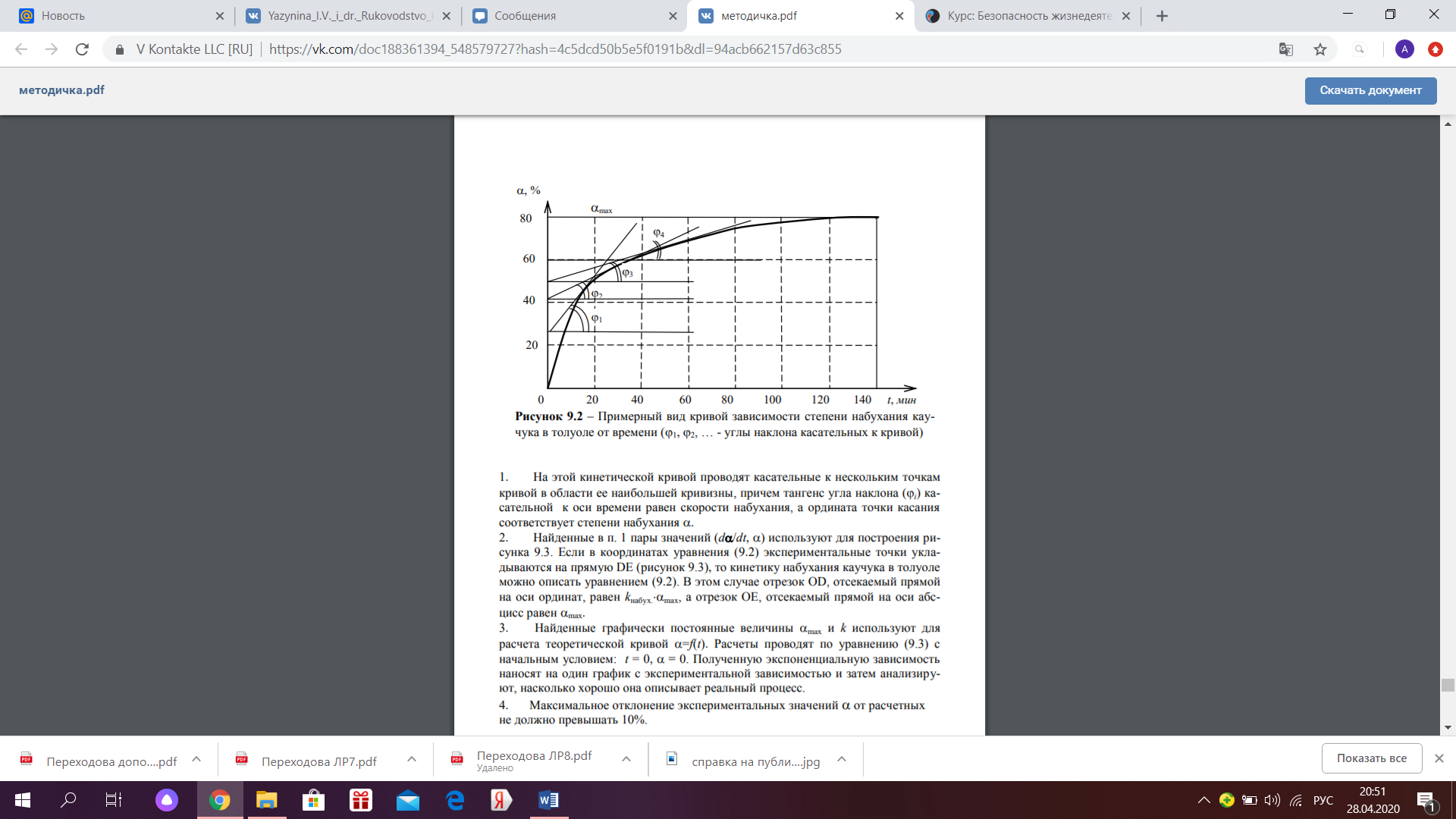 На этой кинетической кривой проводят касательные к нескольким точкам кривой в области ее наибольшей кривизны, причем тангенс угла наклона (i) касательной к оси времени равен скорости набухания, а ордината точки касания соответствует степени набухания 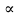 . . Найденные в п. 1 пары значений (d 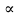 /dt, /dt, 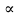 ) используют для построения рисунка 9.3. Если в координатах уравнения (9.2) экспериментальные точки укладываются на прямую DE (рисунок 9.3), то кинетику набухания каучука в толуоле можно описать уравнением (9.2). В этом случае отрезок ОD, отсекаемый прямой на оси ординат, равен ) используют для построения рисунка 9.3. Если в координатах уравнения (9.2) экспериментальные точки укладываются на прямую DE (рисунок 9.3), то кинетику набухания каучука в толуоле можно описать уравнением (9.2). В этом случае отрезок ОD, отсекаемый прямой на оси ординат, равен 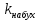 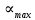 , а отрезок ОЕ, отсекаемый прямой на оси абсцисс равен , а отрезок ОЕ, отсекаемый прямой на оси абсцисс равен 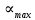 . .Найденные графически постоянные величины 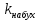 и и 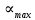 используют для расчета теоретической кривой используют для расчета теоретической кривой 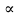 =f(t). Расчеты проводят по уравнению (9.3) с начальным условием: t = 0, =f(t). Расчеты проводят по уравнению (9.3) с начальным условием: t = 0,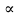 = 0. Полученную экспоненциальную зависимость наносят на один график с экспериментальной зависимостью и затем анализируют, насколько хорошо она описывает реальный процесс. = 0. Полученную экспоненциальную зависимость наносят на один график с экспериментальной зависимостью и затем анализируют, насколько хорошо она описывает реальный процесс. Максимальное отклонение экспериментальных значений 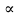 от расчетных не должно превышать 10%. от расчетных не должно превышать 10%.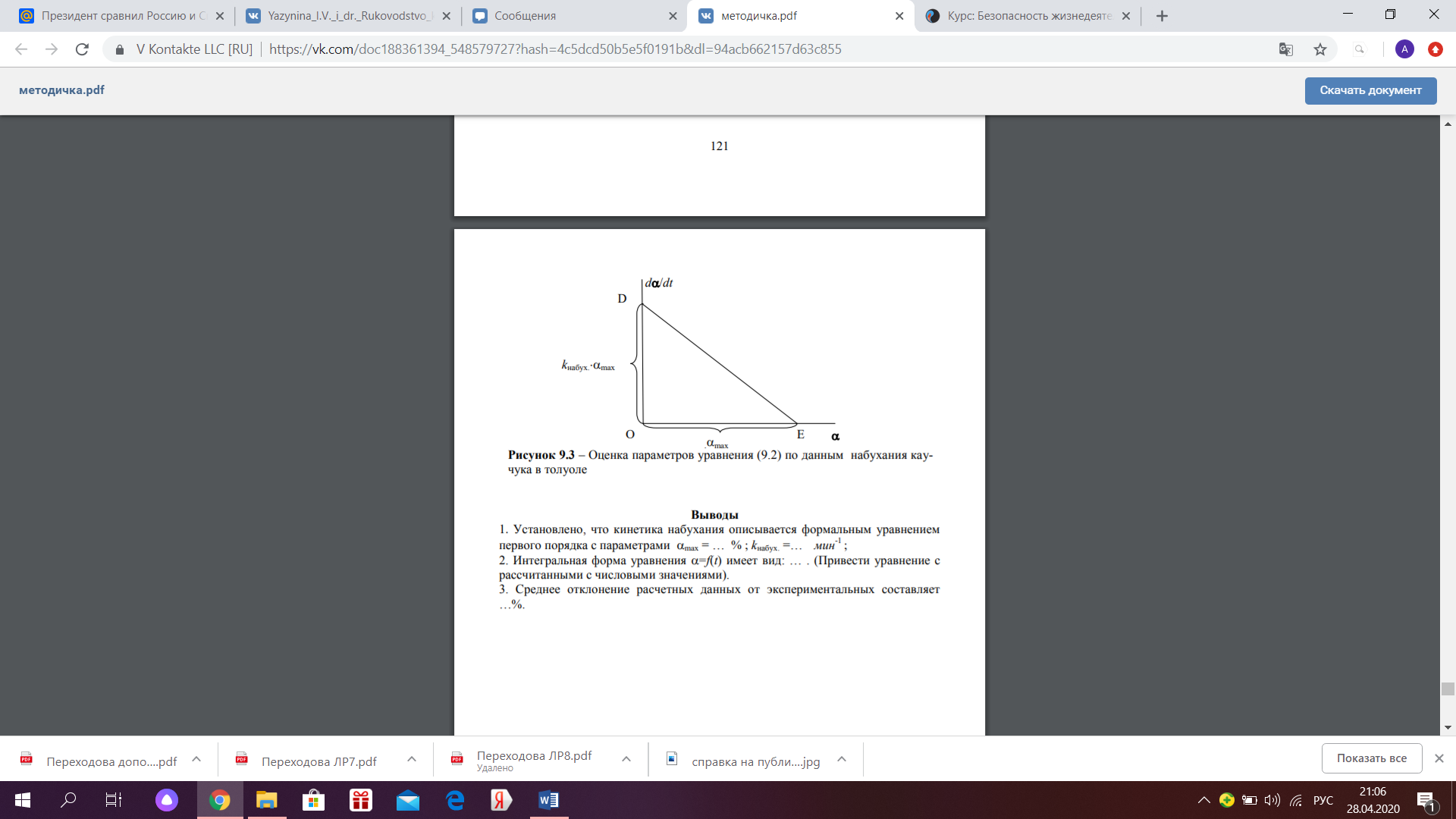 Экспериментальные данные набухания каучука в толуоле при 295К:
Плотность толуола 0,8667 г/ 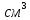 . .Проводим касательные к нескольким точкам кривой в области её наибольшей кривизны, тангенс угла их наклона равен скорости набухания: 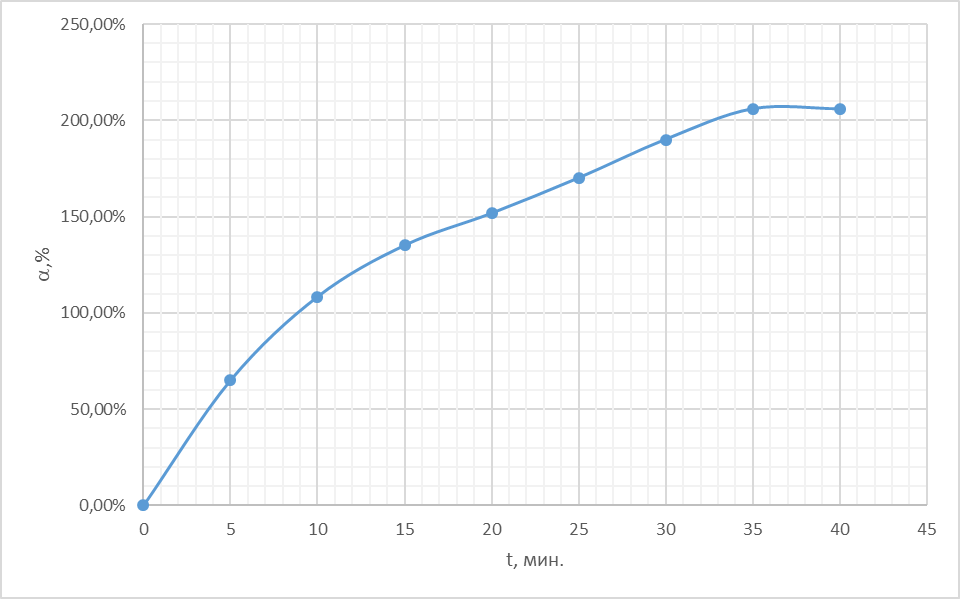 Кривая должна быть строго лекальной т.к. исп метод касательных 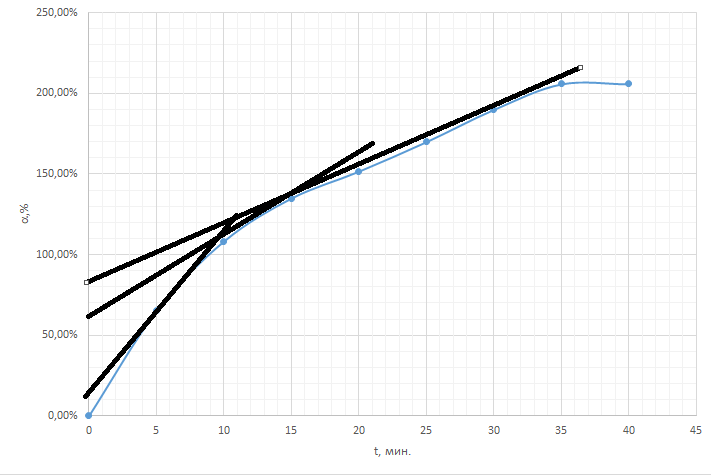 По найденным тангенсам угла наклона касательных и степеням набухания построим график, где по оси абсцисс будет степень набухания, а по оси ординат - скорость набухания. Видно, что с ростом степени набухания, скорость набухания падает, то есть тангенс стремиться к нулю. При степени набухания, равной 2.1, скорость набухания выходит на плато и равна нулю.
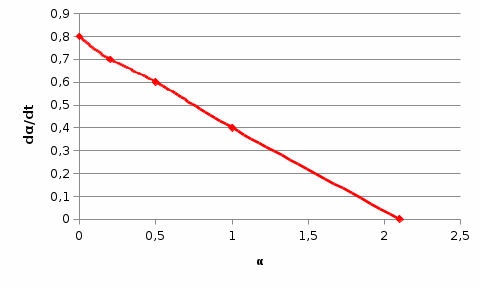 В этом случае отрезок, отсекаемый на оси абсцисс, равен 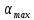 , а отрезок, отсекаемый на оси ординат, равен , а отрезок, отсекаемый на оси ординат, равен 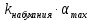 Следовательно, Следовательно, 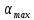 = 1,4, = 1,4,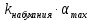 = 1,8, = 1,8, 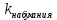 = 1,3. = 1,3.Воспользуемся уравнением зависимости степени набухания от времени и полученными графически константами для построения теоретической кривой =f(t). 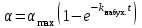 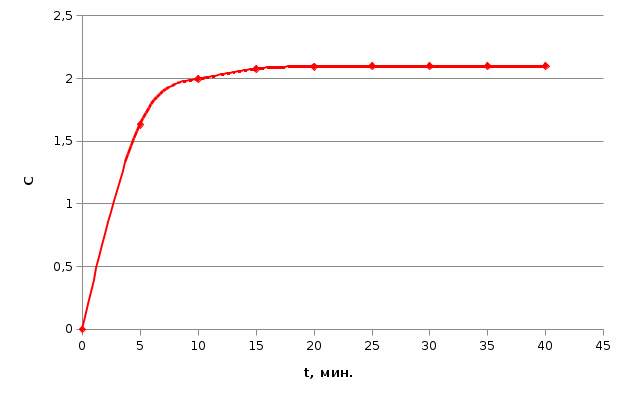 Максимальное отклонение экспериментальных значений от расчетных не превышает 10 %. Вывод: 1. Установлено, что кинетика набухания описывается формальным уравнением первого порядка с параметрами max = 210 % ; kнабух. =0,3 мин-1 ; 2. Интегральная форма уравнения =f(t) имеет вид: 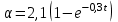 3. Среднее отклонение расчетных данных от экспериментальных составляет 10 %. н  е прокомметировано значение макс ст набухания е прокомметировано значение макс ст набуханияоценка 1,2б Лабораторная работа № 5.1 «Изучение структурной вязкости» Цель работы? Краткая теория: [1, стр. 66-68] В общем виде характер зависимости вязкости от приложенного давления для этих систем показан на рисунке 5.5 З 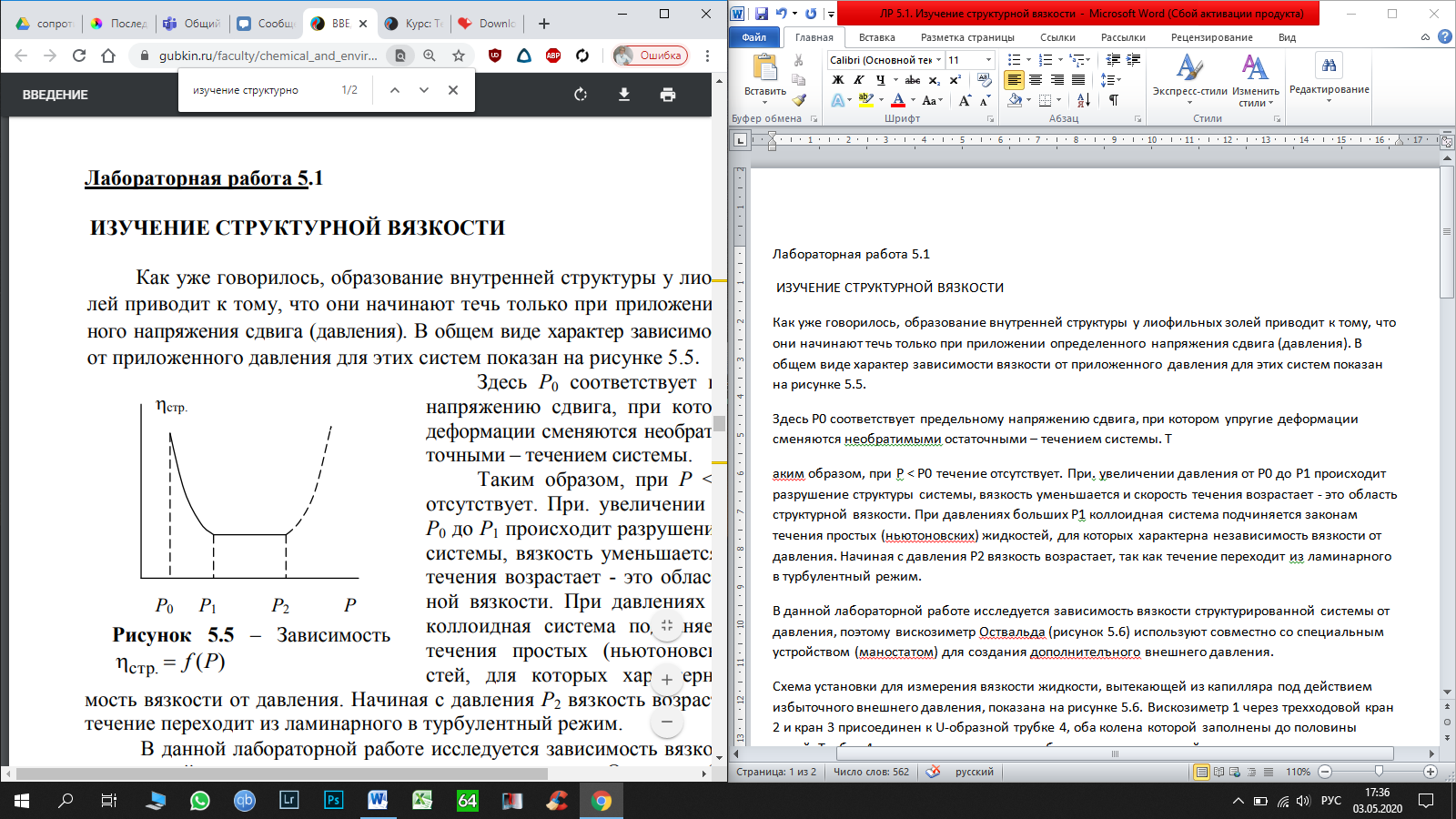 десь P0 соответствует предельному напряжению сдвига, при котором упругие деформации сменяются необратимыми остаточными – течением системы. десь P0 соответствует предельному напряжению сдвига, при котором упругие деформации сменяются необратимыми остаточными – течением системы.Таким образом, при Р В данной лабораторной работе исследуется зависимость вязкости структурированной системы от давления, поэтому вискозиметр Оствальда (рисунок 5.6) используют совместно со специальным устройством (маностатом) для создания дополнителъного внешнего давления. Не рассмотрены уравнения вязкости для ньютон. И неньютон жид Схема установки для измерения вязкости жидкости, вытекающей из капилляра под действием избыточного внешнего давления, показана на рисунке 5.6. Вискозиметр 1 через трехходовой кран 2 и кран 3 присоединен к U-образной трубке 4, оба колена которой заполнены до половины водой. Трубка 4 является маностатом и снабжена отсчетным устройством В качестве объекта исследования выбран р-р КМЦ 0,8. Не раствор, а ДС Порядок работы: 1) определяют время истечения постоянного объема исследуемого раствора в отсутствие избыточного давления (Р=0). 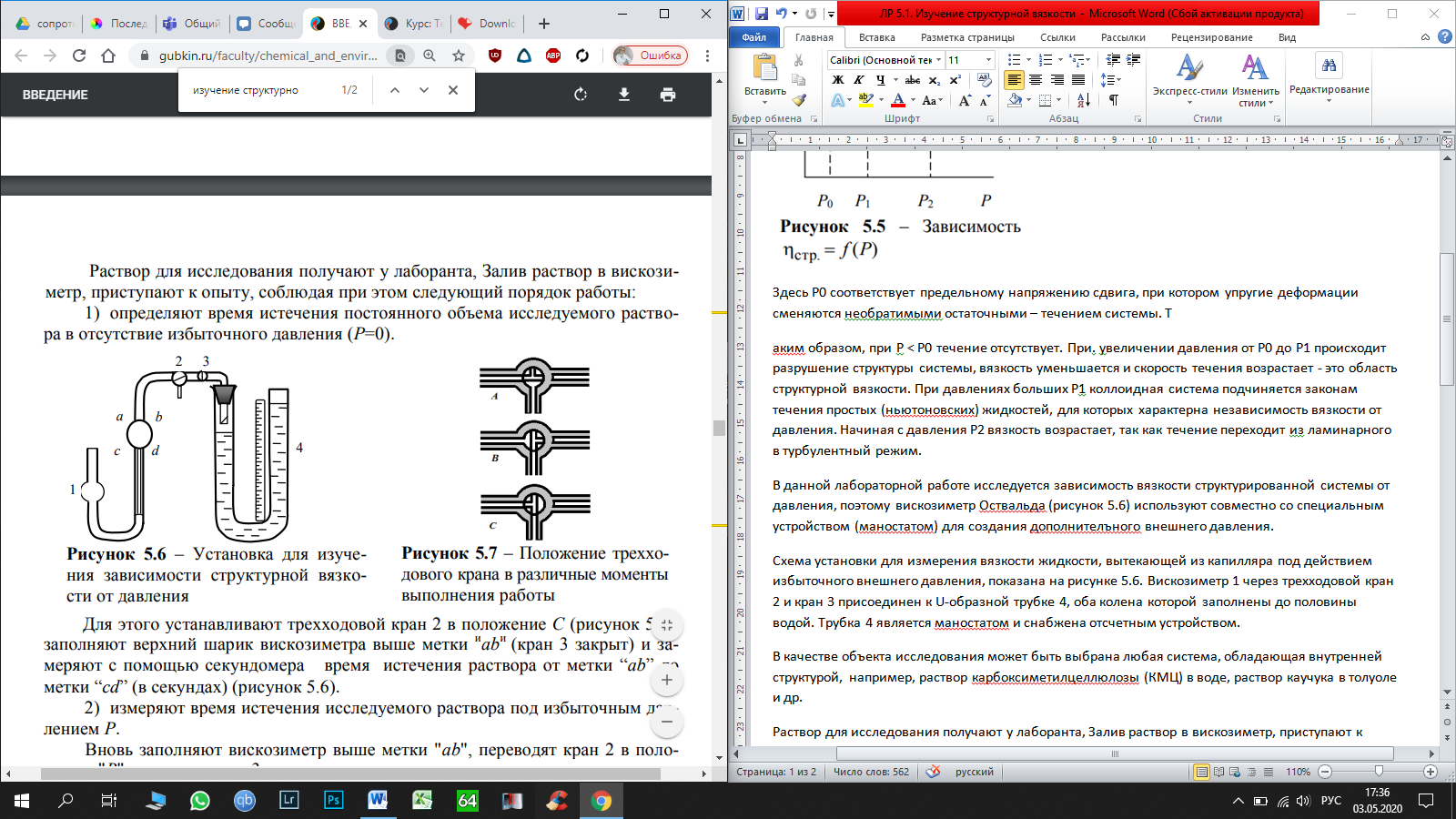 Для этого устанавливают трехходовой кран 2 в положение С (рисунок 5.7), заполняют верхний шарик вискозиметра выше метки и аb и (кран 3 закрыт) и замеряют с помощью секундомера время истечения раствора от метки “аb” до метки “cd” (в секундах) (рисунок 5.6). 2) измеряют время истечения исследуемого раствора под избыточным давлением Р. Вновь заполняют вискозиметр выше метки "аb", переводят кран 2 в положение "В" и, открыв кран 3 с помощью насоса от пульверизатора, создают в маностате избыточное давление 100 мм водн.ст.; быстро закрывают кран 3 и посредством крана 2 (положение А) соединяют маностат с вискозиметром. Открыв кран 3, фиксируют время истечения объема раствора, заключенного между метками "аb" и "cd". Затем аналогичным образом определяют время истечения раствора при избыточном давления 200, 300, 400 мм водн.ст. и т.д. Указанные операции повторяют вплоть до достижения давления 1000 мм водного столба. Полученные при изучении структурной вязкости результаты заносят в таблицу 5.1. По данным таблицы 5.1 строят график зависимости (P+H) от (P+H), характеризующий зависимость структурной вязкости исследуемого раствора от приложенного давления. Таблица 5.1 Зависимость структурной вязкости от давления.
График зависимости (P+H)τ от (P+H), характеризующий зависимость структурной вязкости исследуемого раствора от приложенного давления. 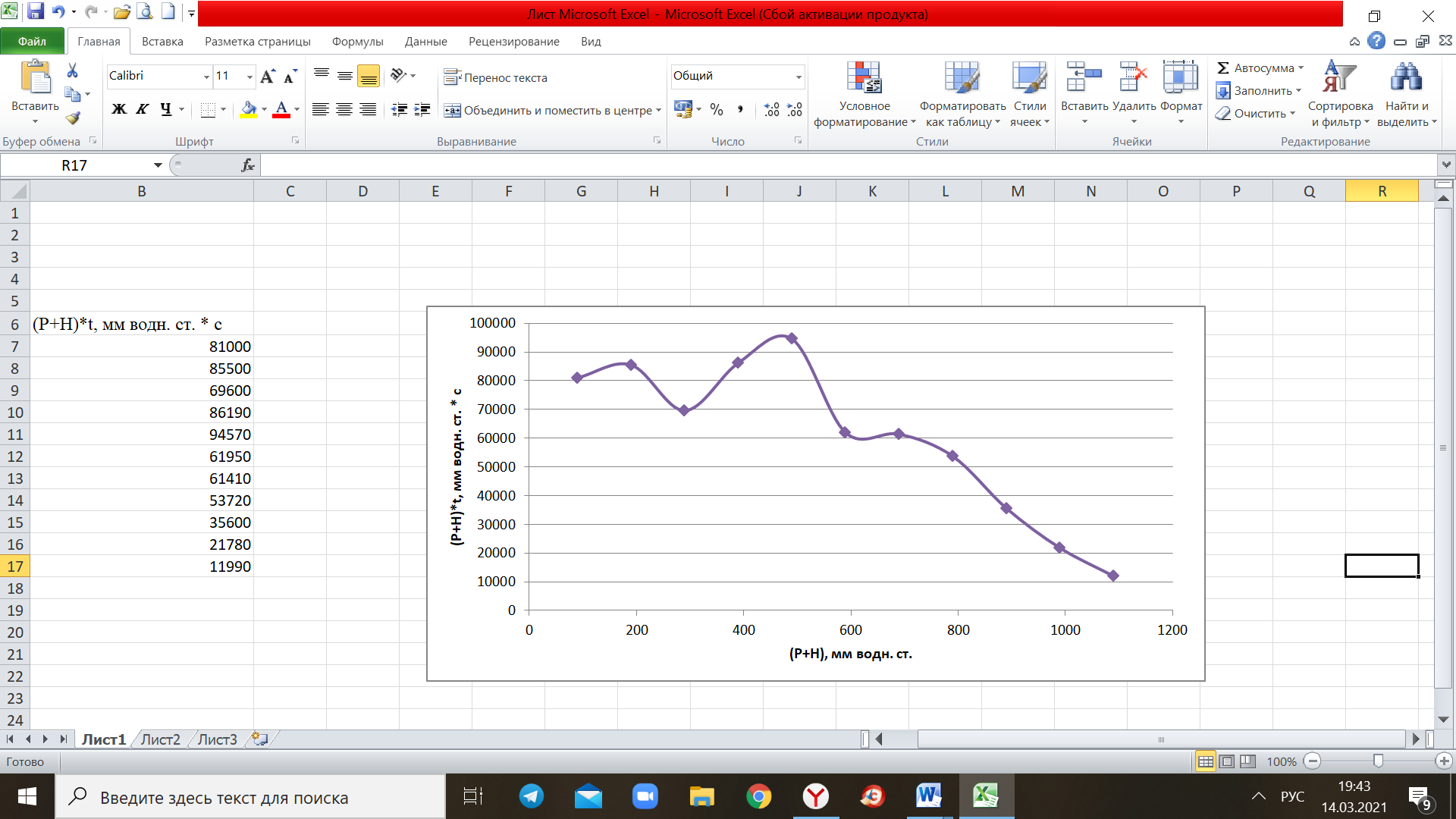 ПЛОХО ПРОВЕДЕН ЭКСПЕРИМЕНТ, НАБЛ.ЮДАЕТСЯ БАРБОТАЭЖ ВОЗДУХА Выводы: В данной лабораторной работе мы изучили зависимость вязкости структурированной системы от давления с помощью вискозиметра Оствальда, который использовали совместно со специальным устройством (маностатом) для создания дополнительного внешнего давления. Не опеределен тип жидкости  Оценка 1,1б Лабораторная работа №8.3 «Изучение адсорбции уксусной кислоты на твердом адсорбенте» Цель работы: Изучение адсорбции на твердом адсорбенте уксусной кислоты из водного раствора, расчет констант уравнения адсорбции Лэнгюмора. Опр. Гэксп. Г расч, Г пред. В. Оценка достоверности расчетов Краткая теоретическая часть: [1, стр. 111-118] Адсорбция из растворов на твёрдом адсорбенте описывается уравнением Лэнгмюра, имеющим вид: 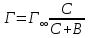 , (1) , (1)где Г – количество вещества, адсорбировонного 1 г адсорбента; С – концентрация раствора после достижения адсорбционного равновесия; Г∞ - предельная адсорбция, соответствующая состояния, когда все активные центры твердого адсорбента заняты молекуоами адсорбируемого вещества (адсорбата). В – константа, характеризующая межмолекулярные взаимодействия между твёрдым адсорбентом и молекулами адсорбируемого вещества (адсорбата). Г∞ и В зависят от прроды адсорбента и адсорбируемого вещества, а В зависит также от температуры.не привиден алгоритм работы Ход работы В качестве адсорбента используют активированный уголь; в качестве адсорбата – уксусную кислоту. Берут 2N уксусную кислоту и готовят в шести колбах следующие растворы кислоты различной концентрации: 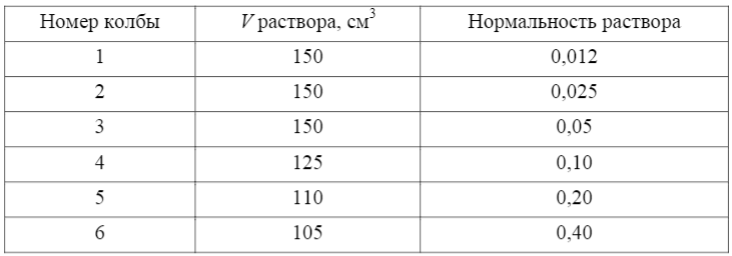 Для вычисления объема 2N уксусной кислоты в см3 (мл), который надо добавить в каждую из шести колб, используют следующее соотношение: N1 V1=N2 V2 , (8.2) где N1 – нормальность исходного раствора кислоты (в нашем случае N1=2); N2 – нормальность получаемого раствора кислоты (например, для колбы №1 N2=0,012); V2 – количество см3 (мл) раствора получаемой кислоты (т.е. для колбы №1 V2=150); V1 - количество см 3 (мл) исходного 2N раствора кислоты Затем в каждую колбочку добавляют по 0,5 г активированного угля (адсорбента), оставляют стоять 10 мин до установления адсорбционного равновесия, взбалтывая по очереди содержимое каждой колбы. Растворы фильтруют и фильтраты оттитровывают 0,1N раствором NaOH, отобрав те же объёмы, как и при титровании исходных растворов кислоты. Чтобы рассчитать начальную (C0) и равновесную (С) концентрацию уксусной кислоты в каждой колбе, необходимо количество см3 NaOH, пошедших на титрование, умножить на следующие величины: 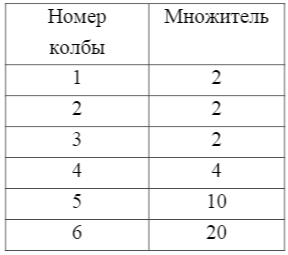 Величину адсорбции Г вычисляют, как разность (C0–С). Полученные значения C0, С, Г, С/Г заносят в таблицу
Обработка результатов Уравнение адсорбции Лэнгмюра после алгебраических преобразований принимает вид: 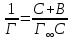 или или 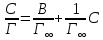 и является уравнением прямой, построенной в координатах С/Г как функция С. Тангенс угла наклона прямой линии на графике зависимости С/Г от С дает значение 1/Г∞, а отрезок, отсекаемый прямой на оси С/Г равен B/Г∞. По найденным из графика значениям 1/Г∞ и B/Г∞ рассчитывают константы уравнения Лэнгмюра Г∞ и B. 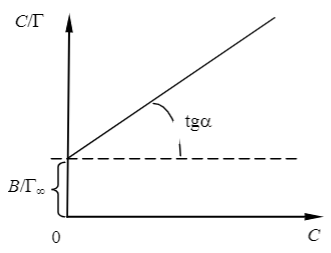 Тангенс угла наклона прямой линии на рисунке 8.1 дает значение 1/Г∞, а отрезок, отсекаемый прямой на оси С/Г равен B/Г∞. По найденным из графика значениям 1/Г∞ и B/Г∞ рассчитывают константы уравнения Лэнгмюра Г∞ и B. Задавая ряд произвольных значений равновесных концентраций C (в пределах концентраций исследуемых растворов) по уравнению (8.1) рассчитывают теоретические значения адсорбции Используя найденные значения констант Г∞, B и полученные данные строят изотерму адсорбции, т.е. зависимость величины адсорбции Г от равновесной концентрации раствора С. На полученный график также наносят опытные значения адсорбции Г при соответствующих концентрациях C, используя данные таблицы. Вычисления и графики: Построим график зависимости С/Г от С по полученным данным 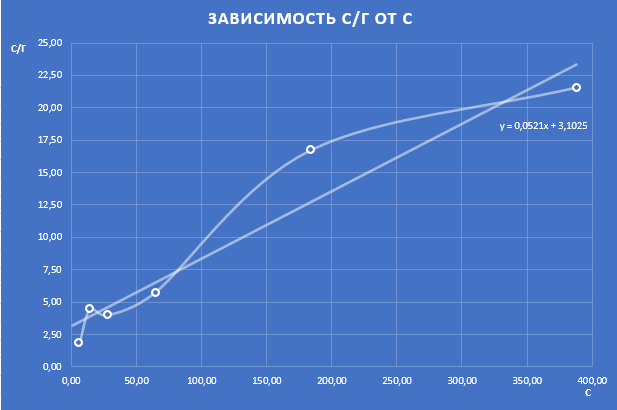 Это не изотермы! С помощью линии тренда определяем тангенс угла наклона линии tgα = 0,0521 Тогда Г∞= 1/ tgα= 1/0,0521 = 19,19385797 Теперь найдем В: В = Г∞ 3,1025 = 19,19385797 3,1025 = 59,54894434 Рассчитаем с помощью полученных констант Г по формуле (1): Г1= 19,193857976,20/ (6,20+59,54894434) = 1,81 Г2= 19,1938579714,20/ (14,20+59,54894434) = 3,70 Г3= 19,19385797 28,00/ (28,00+59,54894434) = 6,14 Г4= 19,1938579764,00/ (64,00+59,54894434) = 9,94 Г5= 19,19385797184,00/ (184,00+59,54894434) = 14,50 Г6= 19,19385797388,00/ (388,00+59,54894434) = 16,64 Теперь построим график зависимости по рассчитанным данным и по данным из таблицы 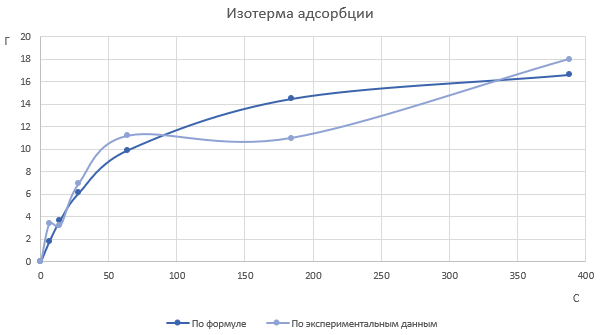 |
