Отчет по выполнению лабораторных работ по дисциплине физическая и коллоидная химия
 Скачать 5.83 Mb. Скачать 5.83 Mb.
|
|
| Номер отсчета | Время от начала опыта t (с) | Отсчет по микроскопу Q*, дел | Деформация коромысла Q дел. |
| 1 | 15 | 0,5 | 0 |
| 2 | 30 | 1,1 | 0,6 |
| 3 | 45 | 1,4 | 0,3 |
| 4 | 60 | 1,7 | 0,3 |
| 5 | 90 | 2,1 | 0,4 |
| 6 | 120 | 2,4 | 0,3 |
| 7 | 150 | 2,7 | 0,3 |
| 8 | 180 | 2,9 | 0,2 |
| 9 | 240 | 3,2 | 0,3 |
| 10 | 300 | 3,3 | 0,1 |
| 11 | 360 | 3,4 | 0,1 |
| 12 | 420 | 3,5 | 0,1 |
| 13 | 540 | 3,6 | 0,1 |
| 14 | 660 | 3,6 | 0 |
| 15 | 780 | 3,7 | 0,1 |
| 16 | 900 | 3,7 | 0 |
| 17 | 1200 | 3,8 | 0,1 |
| 18 | 1500 | 3,8 | 0 |
| 19 | 1800 | 3,9 | 0,1 |
| 20 | 2100 | 3,9 | 0 |
Деформация определена неправильно, Отсчет по микроскопу и деформация должны быть равны
Рассчитываем константу К:
ƞ = 0,001 [Па∙с]
d= 2530
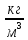 (дисперсной фазы)
(дисперсной фазы)D= 2350
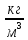 (дисперсионной среды)
(дисперсионной среды)H=9,5 см не приведены ссылки
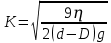
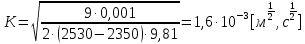
Определим значения
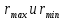
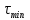 = 60 c
= 60 crmax=
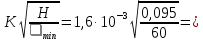 63,67 мкм
63,67 мкмmax= 1200 c
rmin=
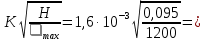 14,24 мкм
14,24 мкмОпределим значения
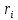
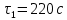
r1=
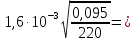 33,25 мкм
33,25 мкм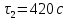
r2=
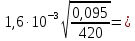 24,06 мкм
24,06 мкм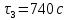
r3=
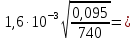 18,19 мкм
18,19 мкмТаблица 7.2
| Время оседания частиц (с) | Радиус частиц (мкм) | Интервал размеров частиц от. Фракций мкм | Длина отрезков между касательными (мм) | Содержание фракций (%) |
| 100 | 15,6 | - | - | 100 |
| 225 | 10,4 | 15,6-10,4 | 4 | 76 |
| 350 | 8,33 | 10,4-8,33 | 0,7 | 13,5 |
| 775 | 5,6 | 8,33-5,6 | 5,2 | 0 |
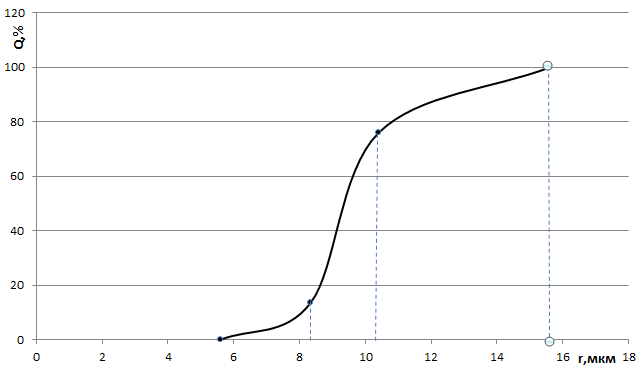
Интегральная кривая распределения частиц дисперсной фазы по размерам
| Интервалы радиусов частиц (мкм) | Содержание фракций (Q)(%) | 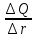 |
| 2,73 | 13,5 | 4,95 |
| 2,07 | 62,5 | 30,19 |
| 5,2 | 24,0 | 4,62 |
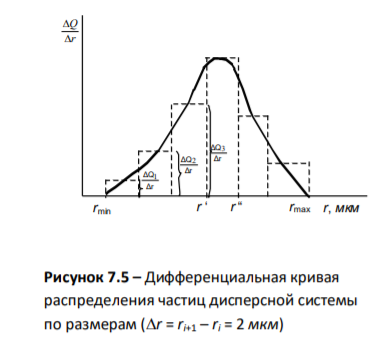
5.Дифференциальная кривая распределения частиц дисперсной фазы по размерам.
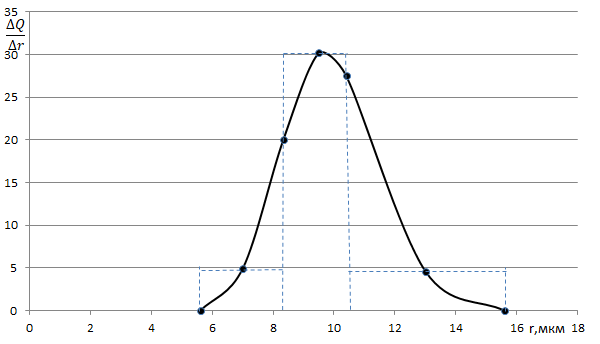
Выводы:
1.Анализируемая дисперсная система содержит от rmin = 5,6мкм до rmax =15,6 мкм
2. Площадь под всей дифференциальной кривой распределения дает общее количество всех частиц дисперсной системы, выраженное в %
3. По дифференциальной кривой распределения можно определить содержание частиц (в %) с радиусами в интервале от ri до ri+1
4. Максимум кривой распределения соответствует наиболее вероятному размеру (радиусу) частиц данной дисперсной системы (т.е. процентное содержание таких частиц в данной дисперсной системе самое большое)
Не показано какая фракция отвечает за устойчивость ДС
ОЦЕНКА 1,0Б

Лабораторная работа №9 «Исследование кинетики набухания полимеров»
Цель работы: по полученным результатам измерений определить Максимльную набухаемость, кинетические параметры набухания.
Краткая теория: [1, стр.118-124]
Максимальная степень набухания (предельное набухание)
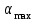 и время ее достижения
и время ее достижения 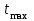 , определяющие способность полимера поглощать низкомолекулярную жидкость при данной температуре, являются важными характеристиками ограниченного набухания. Чем больше молекулярная масса полимера, тем медленнее происходит процесс набухания, т.е. тем больше
, определяющие способность полимера поглощать низкомолекулярную жидкость при данной температуре, являются важными характеристиками ограниченного набухания. Чем больше молекулярная масса полимера, тем медленнее происходит процесс набухания, т.е. тем больше 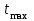
Уравнение, описывающее кинетику ограниченного набухания можно представить в виде дифференциального уравнения первого порядка:
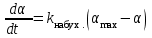 ,(9.2)
,(9.2)где kнабух. – константа скорости набухания; max и – степень набухания при достижении равновесия и к моменту времени t, соответственно.
В результате интегрирования в пределах от =0 до =t получим уравнение кинетики набухания:
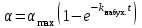 . (9.3)
. (9.3)Скорость набухания в данный момент времени определяется тангенсом угла наклона касательной к кинетической кривой набухания в соответствующей точке. С ростом степени набухания скорость набухания уменьшается.
При набухании полимеров часто наблюдается такое явление как контракция, т.е. уменьшение общего объема системы полимер/растворитель. Контракция происходит на первой начальной стадии набухания и объясняется взаимодействием полимера с растворителем (сольватацией), при котором происходит уплотнение системы. В начальный момент набухания молекулы растворителя, проникая в полимер, образуют первичные сольватные слои. Так, при набухании полярных полимеров, например, желатины, полиакриламида и др., в воде входящую в первичный гидратный слой воду называют «связанной» водой в отличие от «свободной», которая поглощается после формирования первичного гидратного слоя. В результате при малых степенях набухания наблюдается как наибольшее уменьшение общего объема системы – контракция, так и выделение теплоты набухания. Из-за выделения теплоты нагревание системы полимер/растворитель на начальной стадии набухания приводит к замедлению процесса (принцип Ле-Шателье).
Вторая стадия набухания протекает практически без выделения теплоты набухания (внутренняя энергия системы остается постоянной) и контракции системы. Нагревание системы на этой стадии ускоряет набухание, а при неограниченном набухании – и последующее растворение полимера. Вторая стадия набухания обычно отличается от первой значительно бóльшим поглощением низкомолекулярного растворителя. Например, желатина поглощает гидратной («связанной») воды около 50 % масс. (первая стадия), а общее количество воды, которое она может поглотить составляет около 2000 % масс. (в расчете на ее сухую массу). Вторая стадия набухания характеризуется энтропийным эффектом: энтропия растет вследствие перехода в раствор отдельных макромолекул, ослабления связей между ними и увеличения числа их возможных конформаций.
Кинетику набухания обычно изучают объемным или весовым методом.

В приборе, разработанном на кафедре коллоидной химии Ленинградского государственного университета (ЛГУ), скорость набухания определяют объемным методом по разности между первоначальным объемом взятой для опыта жидкости, и объемом оставшейся к данному моменту времени непоглощенной полимером жидкости (рисунок 9.1).
Прибор ЛГУ состоит из двух стеклянных резервуаров, соединенных между собой градуированной стеклянной трубкой С. Резервуар А имеет отверстие D, закрытое пришлифованной пробкой со стержнем на конце, тогда как резервуар В – замкнутый
Через определенные промежутки времени (например, через 5, 10, 20, 30, 50, ... мин) регистрируют объем толуола V. Для этого, поставив прибор вертикально резервуаром А вверх, выжидают ( 1 мин), пока вся жидкость не стечет из резервуара А. Затем отмечают уровень толуола в трубке С и сразу же переводят прибор в наклонное положение. Уменьшение объема жидкости V0 V соответствует объему поглощенного толуола. Затем рассчитывают степень набухания (%)
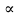 =
= 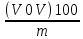 (9.4), где – плотность толуола, г/см 3 (таблица 9.1).
(9.4), где – плотность толуола, г/см 3 (таблица 9.1).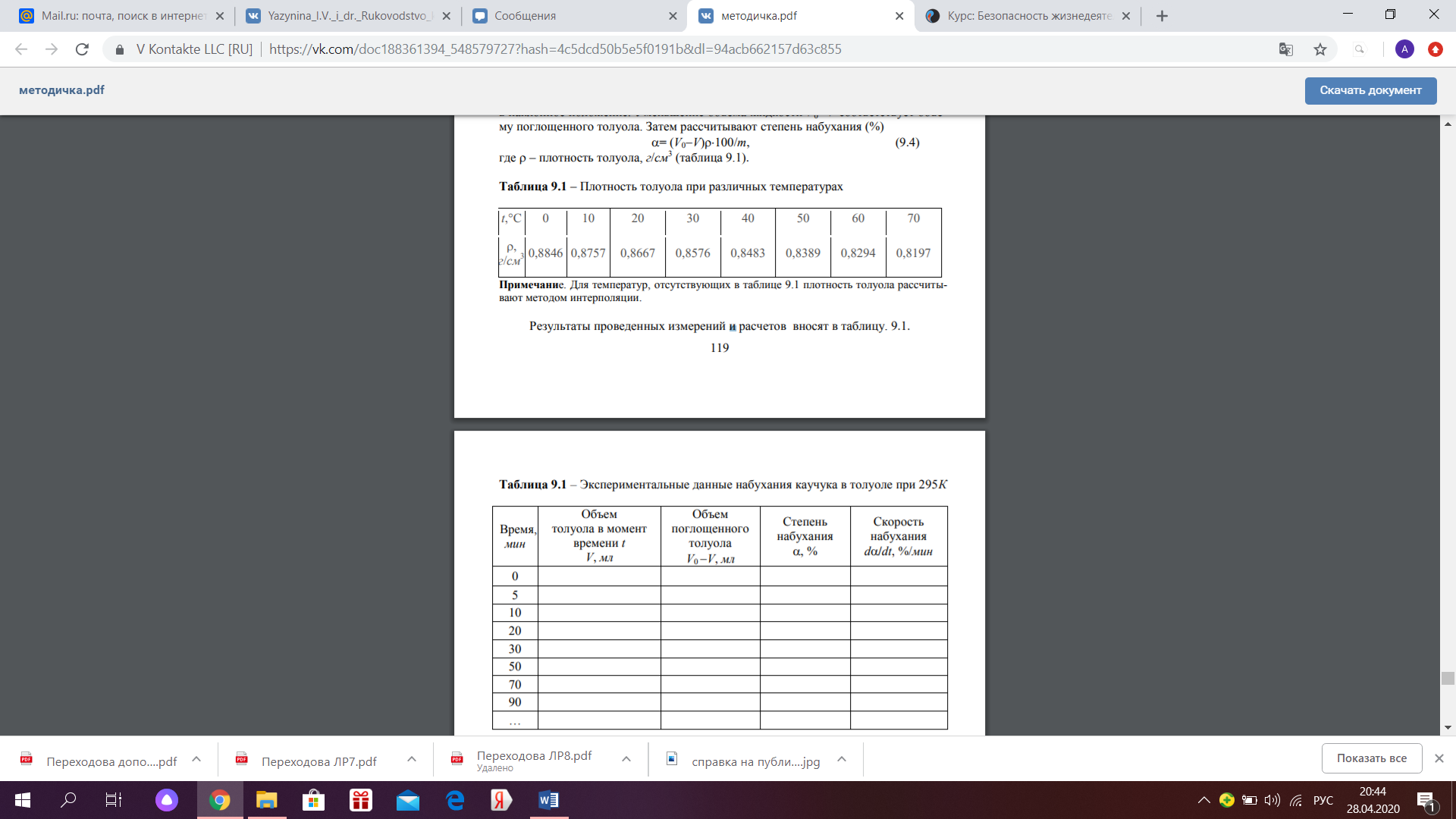

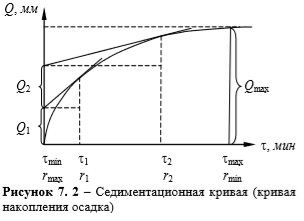
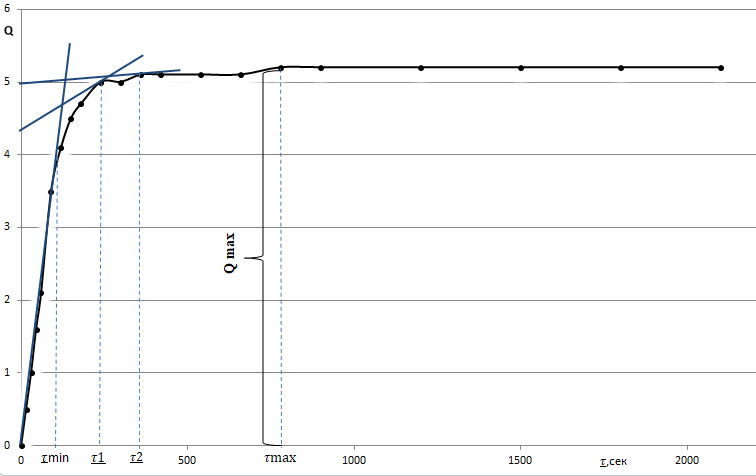
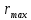 проводят касательную к седиментационной кривой из начала координат. Конец прямолинейного участка кривой, т.е. точка отрыва касательной от седиментационной кривой дает время
проводят касательную к седиментационной кривой из начала координат. Конец прямолинейного участка кривой, т.е. точка отрыва касательной от седиментационной кривой дает время 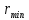 вычисляется по времени
вычисляется по времени 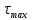 , соответствующему той точке, в
, соответствующему той точке, в 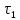 ,
, 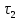 и проводим касательные, продолжая их до пересечения с осью ординат.
и проводим касательные, продолжая их до пересечения с осью ординат.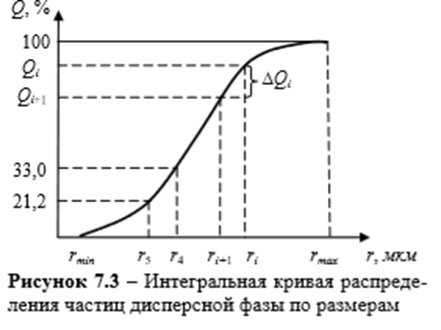
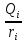 для данных диапазонов размеров частиц ri)
для данных диапазонов размеров частиц ri)