Отчет по выполнению практической работы 1 по дисциплине Теория массового обслуживания
 Скачать 169.25 Kb.
|
|
МИНОБРНАУКИ РОССИИ Федеральное государственное бюджетное образовательное учреждение высшего образования «Юго-Западный государственный университет» Отчет по выполнению практической работы №1 по дисциплине «Теория массового обслуживания» Выполнил: студент группы БТ-81 Сажин Л.А. Проверил: преподаватель Хмелевская А.В. Курск 2022 Практическая работа №1 «Исследование пуассоновского потока» Цель работы Изучение пуассоновского потока и методов аппроксимации теоретическим распределением данных наблюдения за входящим потоком и потоком обслуживания в системах массового обслуживания. Краткая теория Поток требований называют однородным, если: - все требования потока обслуживаются в системе массового обслуживания одинаково; - рассмотрение требований (событий) потока, которые по своей природе могут быть различными, ограничивается рассмотрением моментов времени их поступления. Поток называется регулярным, если события в потоке следуют один за другим через интервалы времени одинаковой длительности. Функция f(х) плотности распределения вероятности случайной величины Т, обозначающей интервал времени между событиями, для регулярного потока имеет вид:  где - дельта функция, t - математическое ожидание случайной величины T Дисперсия интервала между событиями регулярного потока (моментами поступления требований) D[T] равна 0, а интенсивность наступления событий в потоке (среднее число требований в единицу времени) равна 1/ 𝑡̅. Поток называется случайным, если события в потоке следуют один за другим через интервалы времени случайной длительности. Случайный поток может быть описан как случайный вектор, который, в свою очередь, может быть задан одним из двух способов: 1) Функцией распределения моментов наступления событий T1, T2, … , Tn  где ti – значение моментов наступления Ti(i=1,n), 2) Функцией распределения интервалов между наступлением последовательных событий τ1, τ2,… τn:  где i - значения интервалов между событиями τi(i=1,n), В последнем случае моменты наступления событий могут при необходимости быть найдены из рекуррентных соотношений: 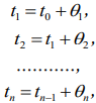 где t0 - момент наступления первого события потока. Поток называется стационарным, если вероятность попадания того или иного числа событий на элементарный участок времени длиной τ зависит только от длины участка и не зависит от того, где именно на оси t расположен этот участок. Поток событий называется потоком без последействия, если для любых непересекающихся участков времени число событий, попадающих на один из них, не зависит от того, сколько событий попало на другой. Поток событий называется ординарным, если вероятность попадания на элементарный участок двух или более событий пренебрежимо мала по сравнению с вероятностью попадания одного события. Поток событий, обладающий всеми тремя свойствами - стационарностью, отсутствием последействия, ординарностью - называется простейшим, или стационарным пуассоновским потоком. Пуассоновский поток событий тесно связан с известным из теории вероятностей распределением Пуассона: число событий потока, попадающих на временной интервал некоторой величины, распределено по закону Пуассона. Если на временной оси t, где наблюдается поток событий, выделить некоторый участок времени длины τ, начинающийся в момент t0 и заканчивающийся в момент t0 + τ, то нетрудно доказать, что вероятность попадания на этот участок ровно m событий выражается формулой:  где а – среднее число событий, приходящееся на участок τ; е – основание натуральных логарифмов (2,71828…), 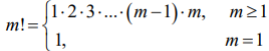 Для стационарного (простейшего) пуассоновского потока величина а равна интенсивности потока λ, умноженной на длину интервала:  где интенсивность, или плотность потока λ есть среднее число событий, приходящихся на единичный временной интервал. В зависимости от физической природы изучаемой системы интенсивность может иметь различную размерность, например, чел/мин, руб/день, кг/час, запросов/сек, документов/сутки, отправлений/сутки и т.д. Функция распределения:  представляющая собой по определению вероятность того, что случайная величина Т (интервал времени между событиями) не превысит значения t, имеет для пуассоновского потока следующий вид:  Такой закон распределения называется показательным (или экспоненциальным) с плотностью λ. Величина λ называется также параметром показательного закона. Математическое ожидание случайной величины Т равна, 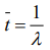 а дисперсия составляет:  Среднеквадратическое отклонение случайной величины Т находится как квадратный корень из дисперсии.  Как нетрудно видеть, математическое ожидание величиныТравно ее среднеквадратическому отклонению, что является характерной особенностью экспоненциального распределения. Таким образом, вероятность появления m событий в заданном промежутке времени описывается пуассоновским распределением, а вероятность того, что временные интервалы между событиями потока не превзойдут некоторого наперед заданного значения, описывается экспоненциальным распределением. Это различные описания одного и того же стохастического процесса. Задания Вариант 16 Поток машин, идущих по шоссе в одном направлении, представляет собой простейший поток с интенсивностью 8 машин в минуту. Шоссе имеет развилку в три направления. Вероятность движения машин в первом направлении равна 0,12, во втором - 0,68, в третьем - 0,20. Определить интенсивности движения автомобилей во всех направлениях. 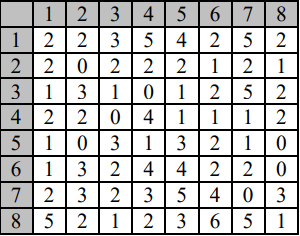 Рисунок 1 – Входящий поток 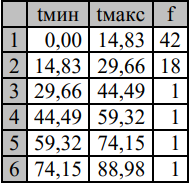 Рисунок 2 – Поток обслуживания Ход работы Анализ данных наблюдения входящего потока Предположим, что проводилось наблюдение за потоком посетителей в отделении банка. Результаты почасового наблюдения представлены в таблице. Определим интенсивность входящего потока покупателей за час работы отделения и, используя критерий Пирсона с уровнем значимости α=0,05 подвергнем проверке гипотезу о том, что поток описывается пуассоновским законом распределения. 1) Сгруппируем данные по числу клиентов банка k, посетивших отделение в течение часа, а результаты представим в виде таблицы:
2) Находим интенсивность потока λ: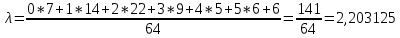 
3)По формуле находим и заносим в строку 𝑓𝑇 теоретические значения частот: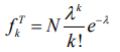 
4)Вычислим и занесем в строку таблицы значения 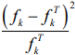 стоящие в числителе выражения под знаком суммы в формуле для наблюдаемого значения критерия Пирсона
В результате получаем наблюдаемое значение 𝑋набл2 = 5,942314 5) По заданному уровню значимости α=0,05 и числу степеней свободы ν = n-2, где n - число групп в ряду (в нашем случае n=9) по таблице значений критических точек 2 распределения находим:  6) Поскольку 𝑋набл2 < 𝑋табл2 (5,942314 < 14,07) не отвергаем гипотезу о том, что входящий поток описывается пуассоновским законом распределения с интенсивностью λ= 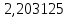 час-1 . Вид теоретической и экспериментальной зависимостей для рассмотренного примера показан на построенной средствами Excel диаграмме, представленной на рисунке 1.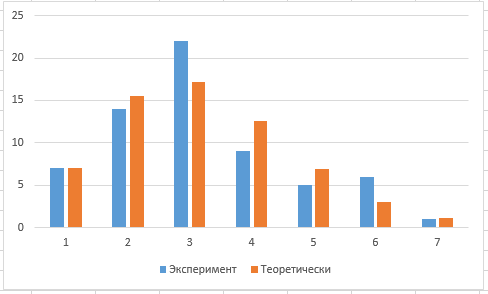 Рисунок 4 – Теоретическая и экспериментальные зависимости Анализ данных наблюдения потока обслуживания Предположим, что проводилось наблюдение за временем обслуживания клиентов отделения банка кассиром, в результате чего получена таблица для частот интервалов следующего вида: Определим среднее время ts и интенсивность μ обслуживания клиентов банка, после чего обоснуем с уровнем значимости α=0,05 гипотезу о том, что время ts распределено по показательному закону, используя для этого критерий Пирсона. 1) Находим среднее значение каждого временного интервала по формуле: 
2) Находим среднее время ts ts = 14,83 и интенсивность μ обслуживания μ = 1/14,83 = 0,06743 В приложении Excel среднее время удобно вычислять, предварительно подсчитав в ячейках отдельного столбца входящие в выражение для среднего времени произведения k fk. 3) По формуле находим теоретические частоты:  где N = 64
4) Вычислим и занесем в отдельный столбец таблицы значения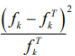 
В результате получаем 𝑋набл2 = 3,897408 5) По заданному уравнению значимости α=0,05 и числу степеней свободы ν = n-2 , где n - число групп в ряду (в нашем случае n=6) в таблице значений критических точек 2 распределения находим  6) Поскольку 𝑋набл2 < 𝑋табл2 (6,9118 < 9,49) не отвергаем гипотезу о том, что время обслуживания клиентов описывается экспоненциальным законом распределения с интенсивностью = 0,06743 мин-1 . Вид теоретической и экспериментальной зависимостей: 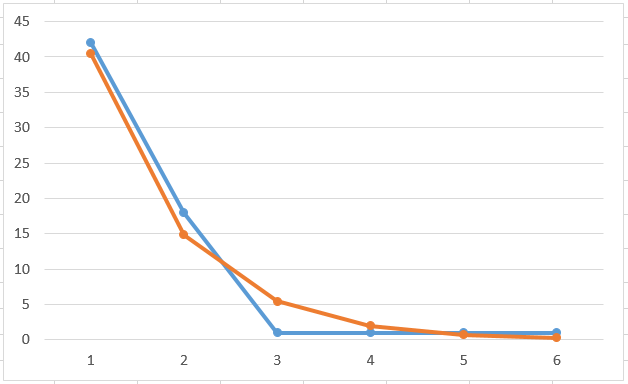 Рисунок 5 – Теоретическая и экспериментальные зависимости Вывод: В ходе выполнения данной практической работы изучил пуассоновский поток и ознакомился с методом аппроксимации теоретического распределения данных наблюдения за входящим потоком и потоком обслуживания в системах массового обслуживания. |