лабароторная. Отчет практическая работа 1 Формы представления чисел в эвм вариант 17 Студент группы п128
 Скачать 57.9 Kb. Скачать 57.9 Kb.
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 |
| ± | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
Для отрицательного числа -3310 используется дополнительный код.
Дополнительный код для числа -3310 получается по следующему алгоритму:
| Прямой код | -3310 | 1000012 |
| Обратный код | Инвертирование | 0111102 |
| | Прибавляем единицу | +0111102 0000012 |
| Дополнительный код | | 0111112 |
Задание №3
Перевести число (3310+170) в двоичную систему счисления с помощью калькулятора (Пуск>Программы>Стандартные). Для этого переключатель «Hex Dec Oct Bin» перевести в положение «Bin», затем переключатель «8 байт 4 байта 2 байта 1 байт» перевести в положение «1 байт». После этого переключатель «Hex Dec Oct Bin» перевести в положение «Dec», ввести число для своего варианта и перевести переключатель «Hex Dec Oct Bin» в положение «Bin». По полученному таким образом внутреннему представлению числа в ЭВМ в формате целого числа с фиксированной запятой 8 бит записать число в десятичной системе счисления.
Решение:
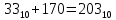 ;
;получен код :
 Номер бита: 1 | 1 | 0 | 0 | 1 | 0 | 1 | 1 |
| +/- | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
Поскольку старший (знаковый) бит равен 1, то это означает, что число отрицательное, что, в свою очередь, означает, что оно представлено в дополнительном коде, поэтому сначала необходимо получить прямой код числа:
| | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 0 |
| + | | | | | | | | 1 |
 Номер бита: | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 1 |
| | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
001101012 = -5310
Задание №4
Определить диапазон представления вещественных чисел в формате с плавающей запятой одинарной точности 32 бита (1 бит знак, 8 бит порядок, 23 бита мантисса), двойной точности 64 бита (1 бит знак, 11 бит порядок, 52 бита мантисса).
Решение:
1) Определим диапазон представления вещественных чисел в формате с плавающей запятой однородной точности 32 бита (1 бит знак, 8 бит порядок, 23 бита мантисса).
Число в формате с плавающей запятой представляется в виде:
A(q) = mqp
где: A – число в формате с фиксированной запятой;
m – мантисса числа; p – порядок A;
q – основание системы счисления, в котором представлено число A.
Формат представления в ЭВМ числа с плавающей запятой одинарной точности имеет следующую структуру:
| Знак 1 бит | Смещённый порядок p 8 бит | Мантисса m 23 бита | ||||||||||||||||||||||||||||||
| | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | |
| 31 | 30 | 23 | 22 | 0 | ||||||||||||||||||||||||||||
Определим максимальное по модулю (без учёта знака) число в этом формате. Такое число должно иметь максимальную мантиссу и максимальный порядок.
Максимальное значение двоичной мантиссы составляет:

(все двоичные мантиссы имеют в целой части единицу, которая при представлении числа ЭВМ отбрасывается, а представляются только 23 разряда после запятой).
Порядок числа представляется в формате целого числа со знаком с фиксированной запятой. Поскольку для представления порядка выделено n = 8 бит, то максимальное его значение составит:
pmax = +2n–1 –1 = 28–1 –1 = +27 – 1 = +127
Таким образом,
│Amax│ = mmax *2pmax = 2*2+127 = 2+128 ≈ 3,40*10+38
Определим минимальное по модулю (без учёта знака) число в этом формате. Такое число иметь минимальную мантиссу и минимальный порядок.
Минимальное значение двоичной мантиссы составляет:
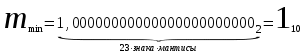
Минимальное значение порядка составляет:
p = –2n–1 = –28–1 = –128
Однако в форматах чисел с плавающей запятой два нижних значения порядка зарезервированы, поэтому минимальное значение порядка составит:
pmin = – (2n–1–2) = –2n–1 +2 = –27 +2 = –128 +2 = –126
Таким образом:
│Amin│ = mmin*2pmin =2–126 ≈ 1,18*2–38
2) Определим диапазон представления вещественных чисел в формате с плавающей запятой однородной точности 64 бита (1 бит знак, 11 бит порядок, 52 бита мантисса).
Формат представления в ЭВМ числа с плавающей запятой одинарной точности имеет следующую структуру:
| Знак 1бит | Смещённый порядок p 11 бит | Мантисса m 52 бита | |||||||||||||||||||||||||||
| | | | | | | | | | | | | | | | | | | | ………………… | | | | | | | | |||
| 63 | 62 | 52 | 51 | 0 | |||||||||||||||||||||||||
Максимальное значение двоичной мантиссы составляет:
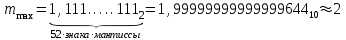
Поскольку для представления порядка выделено n = 11 бит, то максимальное его значение составит:
pmax = +2n–1 – 1 = +210 – 1 = +1023
Таким образом,
│Amax│ = mmax*2pmin = 2*2+1023 ≈ 1,8*2+308
Минимальное значение двоичной мантиссы составляет:

Минимальное значение порядка составляет:
pmin = – (2n–1 – 2) = –210 + 2 = –1024 + 2 = –1022
Таким образом,
│Amin│ = mmin*2pmin = 2–1022 ≈ 2,2*2–308
Ответы на контрольные вопросы к лабораторной работе:
Какие основные формы представления чисел применяются в ЭВМ?
В вычислительных машинах применяются две формы представления чисел:
с фиксированной запятой (точкой);
с плавающей запятой (точкой);
В какой системе счисления представляются числа в ЭВМ?
В ЭВМ применяется двоичная система счисления, т.е. все числа в компьютере представляются с помощью нулей и единиц.
Какие единицы представления данных используются в ЭВМ?
Единицей информации в компьютере является один бит – это двоичный разряд, который может принимать значение 0 или 1.
Отрицательные числа представляются в прямом, обратном и дополнительном кодах и имеют разное изображение.
Как представляются целые положительные и отрицательные числа в ЭВМ?
Положительные целые числа представляются:
число переводится в двоичную систему счисления;
результат дополняется нулями слева в пределах выбранного формата;
последний разряд слева является знаковым, в положительном числе он равен 0.
Отрицательные целые числа представляются:
число без знака переводится в двоичную систему счисления;
результат дополняется нулями слева в пределах выбранного формата;
полученное число переводится в обратный код (нули заменяются единицами, а единицы нулями);
к полученному коду прибавляется 1.
Каков общий вид представления в ЭВМ числа с плавающей запятой?
Число в формате с плавающей запятой представляется в виде :
A(q) = m · qp
A – число в формате с фиксированной запятой;
m – Мантисса числа A; p-порядок числа A;
Q – Основание системы счисления, в котором представлено число A.
Что называют мантиссой и порядком числа?
Число m называют мантиссой – это стандартная форма числа, если оно натуральное или десятичное и удовлетворяет неравенству 1≤m<10
Число n называют порядком числа, записанного в стандартной форме, если оно является целым числом (положительным, отрицательным или нулем)
Какова относительная точность представления чисел в ЭВМ с плавающей запятой одинарной точности и двойной точности?
Диапазон чисел, которые можно записать данным способом, зависит от количества бит, отведённых для представления мантиссы и показателя. На обычной 32-битной вычислительной машине, использующей двойную точность (64 бита), мантисса составляет 1 бит знак + 52 бита, показатель – 1 бит знак + 10 бит. Таким образом получаем диапазон точности примерно от 4,94·10−324 до 1.79·10308 (от 2−52 × 2−1022 до 1 × 21024).
Челябинск

 +33→+1000012
+33→+1000012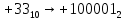 в 8-ми разрядном представлении будет таким:
в 8-ми разрядном представлении будет таким: