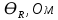Отчет защищен с оценкой преподаватель доц., канд техн наук
 Скачать 59.5 Kb. Скачать 59.5 Kb.
|
|
ГУАП КАФЕДРА № 51 ОТЧЕТ ЗАЩИЩЕН С ОЦЕНКОЙ _________________ ПРЕПОДАВАТЕЛЬ
РАБОТУ ВЫПОЛНИЛ
Санкт-Петербург 2022 Цель работы: - ознакомление с методикой обработки результатов измерений; - определение электрического сопротивления провода; - экспериментальная проверка закона Ома; - определение удельного сопротивления нихрома; - сравнение двух электрических схем; 2. Описание лабораторной установки. 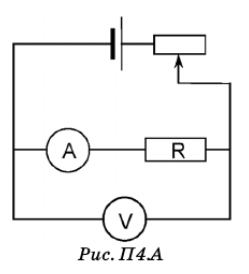 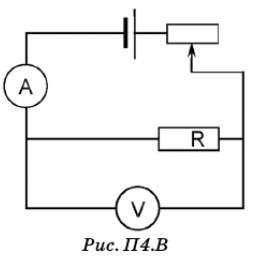 3. Рабочие формулы. Вычисление электрического сопротивления: Закон ома 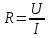 , (1) , (1)Для схемы А 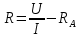 , (2) , (2)Для схемы В 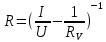 . (3) . (3)В этих формулах R – электрическое сопротивление проводника, U – падение напряжения на проводнике, I – сила тока в проводнике, 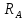 – сопротивление амперметра, – сопротивление амперметра, 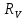 – сопротивление вольтметра. – сопротивление вольтметра. 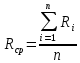 , (4) , (4) где 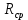 – среднее значение сопротивления, n – число измерений. – среднее значение сопротивления, n – число измерений.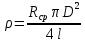 , (5) , (5)где 𝞺 – удельное сопротивление металла, ℓ - длина провода, D – диаметр провода. 4. Результаты измерений и вычислений. Таблица 1.А
Таблица 2. В
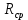 = 6,2 Ом; 𝞺 = 1,40*10-6 Ом·м = 6,2 Ом; 𝞺 = 1,40*10-6 Ом·мПримеры вычислений: По формуле (1) R = 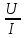 = = 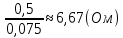 . .По формуле (2) 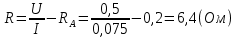 . .По формуле (3) 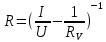 = = 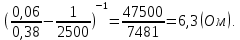 По формуле (4) 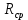 = = 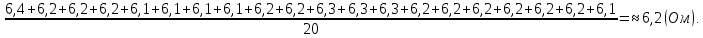 По формуле (5) 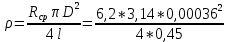 = 1,40*10-6 Ом·м. = 1,40*10-6 Ом·м. Вычисление погрешностей 6.1 Вычисление погрешностей. 6.1.1. 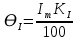 = = 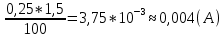 6.1.2. 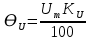 = = 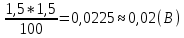 6.1.3. 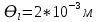 . .6.1.4. 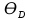 = 0,5*10-5 = 0,5*10-5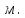 6.1.5. Вывод формулы для систематической погрешности косвенного измерения электрического сопротивления: R = R(U,I) = 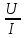 ; ⇒ ; ⇒ 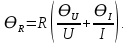 Вычисление по выведенной формуле: 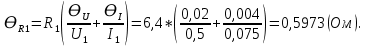 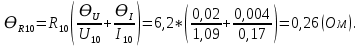 В качестве систематической погрешности итогового результата берем значение, полученное при самом большом токе 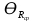 = 0,26 (Ом). = 0,26 (Ом).6.1.6. Вывод формулы для систематической погрешности удельного сопротивления металла. 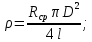 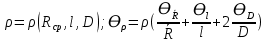 . .Вычисления по выведенной формуле: 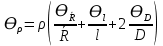 = 1,40*10-6 * ( = 1,40*10-6 * (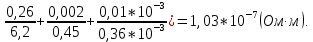 6.2. Случайные погрешности. 6.2.1. Средняя квадратичная погрешность отдельного измерения 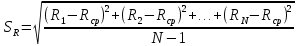 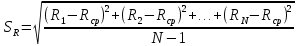 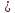 0,077 (Ом) 0,077 (Ом)6.2.2 Среднеквадратичное отклонение: 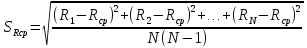 = 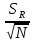 . .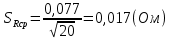 В данной работе проводится измерение неслучайных по своей природе физических величин: электрического сопротивления провода – R и удельного сопротивления нихрома – 𝞺, поэтому, проверяем неравенства 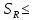 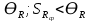 . .0,077 Ом ˂ 0,26 Ом, т.е 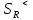 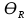 ; ;0,017 Ом ˂˂ 0,26 Ом, т.е 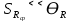 . . Получившиеся неравенства говорят о том, что в измерениях, скорее всего, нет грубых ошибок и промахов. 6.2.3 Случайные погрешности удельного сопротивления: 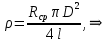 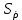 = = 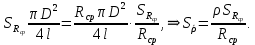 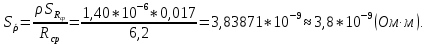 6.3 Полная погрешность. В случае, когда измеряются неслучайные по своей природе физические величины, случайные погрешности уже учтены в систематических. Объединять их в полную погрешность не надо. Полная погрешность равна систематической погрешности. 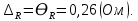 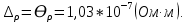 7. Выводы. Ознакомился с методикой обработки результатов косвенных измерений. Электрическое сопротивление провода R = ± Ом с вероятностью Р = 95%. Удельное сопротивление нихрома 𝞺 = ( ± ) · 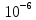 Ом·м с вероятностью Р = 95%. Ом·м с вероятностью Р = 95%.Экспериментально определённое значение 𝞺 в пределах погрешности совпадает с табличным значением нихрома 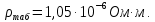 Их приведенных опытов видно, что каждое сопротивление в табл. 1.А, В отличается от 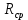 меньше, чем на систематическую погрешность меньше, чем на систематическую погрешность 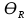 .Это обозначает, что электрическое сопротивление не зависит от протекающего тока и от падения напряжения на нем, т.е справедлив закон Ома. .Это обозначает, что электрическое сопротивление не зависит от протекающего тока и от падения напряжения на нем, т.е справедлив закон Ома. Учет сопротивления амперметра приводит к поправке 0,2 Ом, учет сопротивления вольтметра приводит к поправке 0,02 Ом. Поскольку результат приходится округлять до десятых долей ома, поправку на сопротивление вольтметра по формуле (3) можно не делать. Значит для схемы В электрическое сопротивление можно вычислять по закону Ома без поправок. |