мму. ММУ. Отчет защищен с оценкой преподаватель канд физ мат наук

• Название: Отчет защищен с оценкой преподаватель канд физ мат наук
• Дата: 21.12.2021
• Размер: 10.14 Kb.
• Имя файла: ММУ.docx
• Тип: Отчет; #313117

ГУАП

КАФЕДРА № 31

ОТЧЕТ
ЗАЩИЩЕН С ОЦЕНКОЙ

ПРЕПОДАВАТЕЛЬ

канд. физ.-мат. наук				В. Г. Курбанов
должность, уч. степень, звание		подпись, дата		инициалы, фамилия

ОТЧЕТ О ПРАКТИЧЕСКОЙ РАБОТЕ №1

Экстремум функции многих переменных

по курсу: МАТЕМАТИЧЕСКИЕ МЕТОДЫ В УПРАВЛЕНИИ

РАБОТУ ВЫПОЛНИЛ

СТУДЕНТ ГР. №	3811				Образцов А.С.
			подпись, дата		инициалы, фамилия

Санкт-Петербург

2021

1. Цель работы

Изучить способы решения задач по отысканию экстремума функции многих переменных.
2. Задание на лабораторную работу

Найти точки экстремума для следующей функции многих переменных: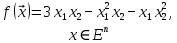


3. Результаты выполнения задания

Найдём частные производные данной функции и приравняем их к нулю: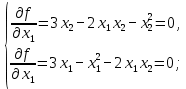

(1)

Вычтем второе уравнение из первого, тогда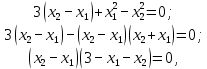



откуда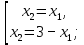

(2)

Подставляя эти выражения в первое уравнение системы (1), получаем: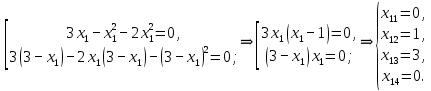



Подставляя полученные значения в (2), получаем: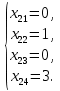



Таким образом, имеем четыре стационарные точки: (0,0), (1,1), (3,0) и (0,3).

Для выяснения характера найденных стационарных точек с помощью критерия Сильвестра составим матрицу вторых производных для данной функции: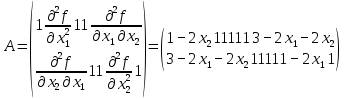

(3)

Подставляя в (3) координаты найденных стационарных точек, получаем: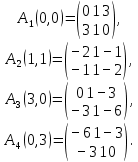



Поскольку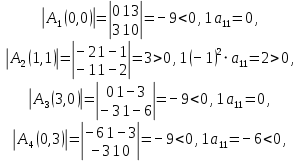



то матрица A₁ является неположительно определённой, А₂ — отрицательно определённой, А₃ — неположительно определённой, А₄ — не является положительно или отрицательно определённой. Следовательно:

1) Точка (0,0) удовлетворяет необходимому условию максимума, однако непосредственное рассмотрение функции f вблизи этой точки показывает, что точка (0,0) не является точкой экстремума функции f;

2) Точка (1,1) является точкой максимума функции f;

3) Точка (3,0) также удовлетворяет необходимому условию максимума, однако непосредственное рассмотрение функции f вблизи этой точки показывает, что точка (3,0) не является точкой экстремума функции f.

4) Точка (0,3) не является точкой экстремума функции f.

Таким образом, функция f имеет одну точку экстремума — точку максимума (1,1).
4. Выводы

В результате выполнения лабораторной работы был изучен метод решения задачи по нахождению точек экстремума функции многих переменных. Для заданной функции двух переменных с помощью необходимого условия экстремума были найдены стационарные точки, характер которых был определён с помощью достаточного условия — критерия Сильвестра.