бараш 2. Относительные методы оценки численности стада рыб. Учет на основе анализа общих уловов и улов на рыбоводное усилие
 Скачать 16.45 Kb. Скачать 16.45 Kb.
|
|
Глава 1 Относительные методы оценки численности стада рыб. Учет на основе анализа общих уловов и улов на рыбоводное усилие После того как промысел достигнет определенной интенсивности, колебания уловов обычно отражают изменения численности промыслового стада рыбы. Следовательно, при более или менее стабильной интенсивности рыболовства по колебаниям уловов можно судить о колебаниях численности стада рыбы. Колебания общего вылова (годового улова) обычно могут служить довольно надежным критерием изменения численности стада. Изменения уловов за более короткие промежутки времени часто могут отражать не столько изменения в численности и биомассе стада, сколько сдвиги в ходе годового цикла рыбы в связи с режимом данного года. Поскольку промысел обычно бывает приурочен к определенным фазам годового цикла (миграции, нерест, нагул и т.д.), то сдвиги этих сезонных явлений могут сильно отражаться на величине уловов за тот или иной отрезок времени. Естественно, что оценка изменений численности и биомассы стада по колебаниям общих уловов требует учета и технико-экономических сторон рыболовства. Совершенствование техники рыболовства также приводит к относительному увеличению вылова. Большое значение имеют и экономические причины: наличие спроса, себестоимость добычи и обработки рыбы, наличие рабочей силы, перерабатывающих баз и т.д. Все это отражается на величине уловов. Таким образом, колебания уловов обычно отражают изменения численности и биомассы стада рыбы при неизменной интенсивности рыболовства. Поскольку практически интенсивность рыболовства лишь очень редко остается стабильной, ее изменения приходится учитывать при анализе колебаний уловов. Анализ общих уловов позволяет проследить как общую тенденцию изменения биомассы стада, так (при наличии раздельного учета рыб разного размера) и динамику примерного соотношения взрослого стада и пополнения; на основе анализа общих уловов удается выявить многолетние колебания величины стада и степень влияния рыболовства. Только хорошо налаженная промысловая статистика может быть использована для анализа динамики стада промысловых рыб. Хорошо налаженная статистика – это показатель культуры рыболовства. Очень важно, чтобы группировка статистических данных соответствовала естественным внутривидовым группировкам промысловых рыб (например, летняя и осенняя кета, ивановская и егорьевская беломорская сельдь и т.п.) и чтобы на основе анализа статистики уловов можно было выявить динамику уловов отдельных локальных стад. Хорошо 125 налаженная статистика уловов обеспечивает более точную оценку рыбных ресурсов, более надежные прогнозы их изменений, а в конечном итоге все это значительно повышает эффективность рыболовства. Основным показателем, наиболее широко используемым для оценки состояния стада и при составлении прогнозов колебаний численности и биомассы промысловых рыб, является улов на рыболовное усилие. Под уловом на рыболовное усилие понимается величина улова тем или иным орудием лова или кораблем в единицу времени. Характер применяемого показателя улова на рыболовное усилие зависит от специфики промышляемой рыбы и от применяемых орудий рыболовства. При анализе уловов на час траления очень важное значение имеют скорость траления и величина трала, что прямо связано с техническими показателями корабля и судового двигателя. Оценка запаса по уловам закидного невода (1): 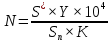 где, N – численность рыб, шт. S∗ – площадь водоема, доступная для облова закидным неводом, га γ – улов невода за съемку, шт. Sn – обловленная неводом площадь водоема за съемку, га k – коэффициент уловистости, равен (2) 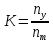 где nm – количество меченых рыб, nу – количество вторично пойманных меченых рыб. Для того, чтобы улов на рыболовное усилие отражал действительные изменения, происходящие в численности и биомассе стада рыбы, необходимо кроме достаточного количества наблюдений, позволяющих получать статистически достоверные результаты, учитывать ряд моментов, связанных как с состоянием и поведением рыбы, так и с состоянием погоды и с техническими условиями промысла. Естественно, уловистость отдельных орудий лова меняется в отношении многих рыб в разное время суток, и это приходится учитывать при анализе. 1.1. Математические модели динамики численности рыб Математическое моделирование – это метод, при помощи которого можно выявить механизм процесса и понять его структурные особенности – установить параметры анализируемой совокупности. Математическое моделирование при наличии большого цифрового материала позволяет использовать счетно-решающие и моделирующие устройства для более быстрой и надежной обработки материала и для более разностороннего анализа собранных данных. Попытки математического моделирования динамики популяций предпринимались неоднократно, начиная с работ Росса (Ross, 1910) о динамике зараженности малярией, В.А. Кевдина (1915), Ф.И. Баранова (1918) и А.Н. Державина (1922) о динамике популяций рыб. Все существующие математические модели динамики популяций в известной степени схематично можно разделить на четыре группы: 1) основанные на отношении пища – потребитель, где рыба выступает в роли потребителя; 2) основанные на отношении хищник – жертва, где рыба выступает в качестве жертвы. В эту же группу включаются модели, где в роли хищника выступает промысел; 3) основанные на предположении о закономерном количественном отношении родительского стада и потомства; 4) в которых рассматривается несколько взаимодействующих величин – пополнение, рост, убыль. Существуют также модели по изучению пространственного распределения рыб во время миграций. По принципу построения математические модели могут быть объединены в две группы: 1) с «непрерывным временем», базирующиеся на дифференциальных уравнениях, и 2) основанные на дискретном времени и строящиеся на основе структурных схем. Возможны и комбинированные дискретно-непрерывные модели Впервые дифференциальные уравнения в анализе динамики популяций были использованы Россом (1910), ряд его положений, в первую очередь положение о средней мгновенной скорости заражения, вошли в модельные построения Ф.И. Баранова (1918). Ф.И. Баранов был первым исследователем, использовавшим дифференциальные уравнения для оценки динамики численности рыб. В дальнейшем дифференциальными уравнениями для моделирования динамики популяций рыб пользовались Бивертон и Холт (Beverton R.J. and Holt S.J., 1957), Гулланд (Gulland, 1964) и многие другие исследователи. Принцип построения моделей с дискретным временем основан на анализе в первую очередь возрастной структуры популяции, соотношения остатка и пополнения и периодичности нереста. На этом принципе строились модели А.Н. Державина (1922), Н.Л. Чугунова (1935), Г.Н. Монастырского (1940, 1952), Т.Ф. Дементьевой (1952), Г.В. Никольского (1961, 1963 и др.), Ю.Е. Лапина (1961) и многие другие. |
