Главная страница
Навигация по странице:

  • Предел функции (по Гейне)

  • пределом функции

  • .

  • Док-во: https://1cov-edu.ru/mat-analiz/predel-posledovatelnosti/svojstva-neravenstv/teorema-o-dvuh-militsionerah/o_militsionerah

    		•

    Коллоквиум по математическому анализу. колок.pdf. Ответ 1 Действительное число a называется пределом числовой последовательности


    Скачать 0.8 Mb.
    НазваниеОтвет 1 Действительное число a называется пределом числовой последовательности
    АнкорКоллоквиум по математическому анализу
    Дата18.11.2021
    Размер0.8 Mb.
    Формат файлаdocx
    Имя файлаколок.pdf.docx
    ТипДокументы
    #275738

    Определения

    1. Предел числовой последовательности (три определения)

    Ответ:

    1)Действительное число a называется пределом числовой последовательности { xn } , если вне любой окрестности точки a находится лишь конечное число членов данной числовой последовательности.
    2)Число a называется пределом последовательности {xn}, если для любого ε > 0 существует такой номер Nε, что для любого n≥Nε выполняется неравенство |xn−a|<ε.
    3) Действительное число a есть предел числовой последовательности { xn }, если какова бы ни была окрестность этого числа, все члены данной ч.п., начиная с некоторого, попадают в эту окрестность.


    1. Бесконечно малая последовательность

    Ответ:

    Бесконечно малая последовательность {αn} – это сходящаяся последовательность, предел которой равен нулю: limn→∞ αn=0.


    1. Бесконечно большая последовательность

    Ответ:

    Последовательность {xn} называется бесконечно большой, если для любого δ>0 cуществует такой номер Nδ, что для всех n ≥ Nδ выполняется неравенство |xn| > δ. В этом случае пишут  limn→∞(xn)=∞ и говорят, что последовательность имеет бесконечный предел.


    1. Предел функции (два определения)

    Ответ:

    1)Предел функции (по Гейне)

     

    при ее аргументе x, стремящемся к x0 – это такое конечное число или бесконечно удаленная точка a, для которой выполняются следующие условия:
    1) существует такая проколотая окрестность U(x0)  точки x0, на которой функция f (x) определена;
    2) для любой последовательности { xn }, сходящейся к  x0: limn→∞(xn)=X0
    ,
    элементы которой принадлежат окрестности U(x0)   , последовательность { f (xn) } сходится к a:
    .

    Число A называется пределом функции f(x) в точке a, если эта функция определена в некоторой проколотой окрестности точки α, то есть ∃δ0>0: U˙δ0(a)⊂D(f), и для любой последовательности {xn }, сходящейся к a и такой, что xn∈Uδ0(a)xn∈Uδ0(a) для всех n∈N, соответствующая последовательность значений функции {f(xn)} сходится к числу A
    2) Число A называется пределом функции f(x) в точке a, если эта функция определена в некоторой окрестности точки a, за исключением, быть может, самой точки a, и для каждого ε>0 найдется число δ>0 такое, что для всех x, удовлетворяющих условию |x−a|<δ, x≠a, выполняется неравенство |f(x)−A|<δ. В этом случае пишут limx→af(x)= A или f(x)→Af(x)→A при x→ a.

    1. Функция

    Ответ:

    Функциейy = f(x) называется закон (правило, отображение), согласно которому, каждому элементу x множества X ставится в соответствие один и только один элемент y множества Y.



    1. Приращение функции

    Ответ:

    Пусть функция y=f(x) определена в точках x0 и x1. Разность x1−x0 называют приращением аргумента (при переходе от точки x0 к точке x1), а разность f(x1)−f(x0) называют приращением функции.


    1. Непрерывность функции в точке (три определения)

    Ответ:



    1. 8. Точки разрыва, их классификация

    Ответ: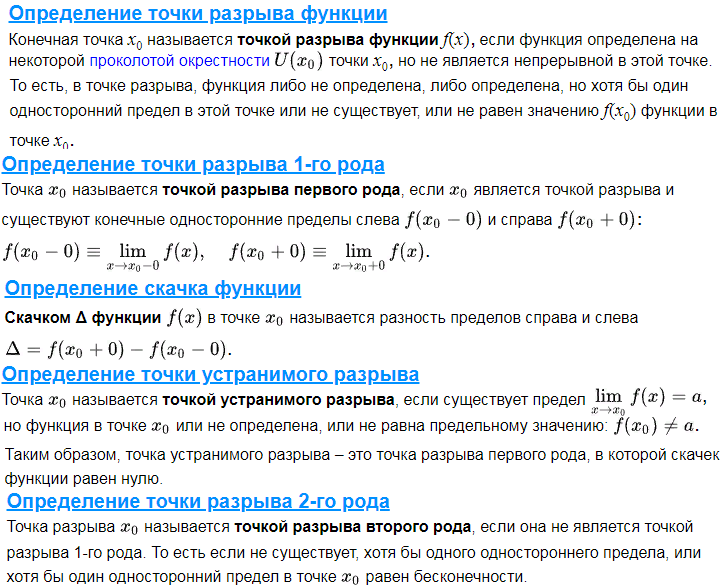




    Теоремы

    1. о единственности предела последовательности



    1. о предельном переходе в неравенствах

    Теорема. Если элементы сходящейся последовательности {xn}, начиная с некоторого номера, удовлетворяют неравенству xn ≥ b (xn ≤ b), то и предел a этой последовательности удовлетворяет неравенству a ≥ b (a ≤ b).

         Доказательство. Пусть все элементы xn, по крайней мере начиная с некоторого номера, удовлетворяют неравенству xn ≥ b. Требуется доказать неравенство a ≥ b. Предположим, что a < b. Поскольку a - предел последовательности {xn}, то для положительного ε = b - a можно указать номер Nтакой, что при n ≥ N выполняется неравенство |xn - a| < b - a. Это неравенство эквивалентно следующим двум неравенствам: -(b - a) < xn - a < b -a. Используя правое из этих неравенств, получим xn < b, а это противоречит условию теоремы. Случай xn ≤ b рассматривается аналогично. Теорема доказана.

    1. о двух полицейских (для последовательностей)

    Если два милиционера {xn} и {zn} идут в милицейский участок a:   , то оказавшийся между ними подозреваемый {yn},  xn ≤ yn ≤ zn, также придет в этот участок
    Теорема о двух милиционерах (для последовательностей). Если последовательность {xn}  такая, что для любого натурального значения  n xn ≤ yn ≤ zn, и  , то и 

    Док-во: https://1cov-edu.ru/mat-analiz/predel-posledovatelnosti/svojstva-neravenstv/teorema-o-dvuh-militsionerah/#o_militsionerah


    1. о сходимости монотонной последовательности



    1. неравенство Бернулли





    https://1cov-edu.ru/mat-analiz/nepreryvnost-funktsii/neravenstva-i-lemma-bernulli/#proof1

    1. последовательность n 1 n n 1 y 1          имеет предел

    2. о пределе суммы двух последовательностей

    Сумма сходящихся последовательностей {xn} и {yn} представляет собой сходящуюся последовательность, предел которой равен сумме пределов последовательностей {xn} и {yn}.

    Доказательство. Предположим, что последовательности {xn} и {yn} сходятся к пределам а и b соответственно. Тогда в силу того что xn=a+an будут справедливы соотношения
    xn=a+an,yn=b+bn, (6),
    в которых an и bn представляют собой элементы некоторых бесконечно малых последовательностей {an} и {bn}. Из (6) вытекает, что (xn+yn) - (a -b)=an+bn. (7)

    Т.к. сумма {an+bn} двух бесконечно малых последовательностей {an} и {bn} представляет собой бесконечно малую последовательность, то из соотношения (7) вытекает в силу определения, что последовательность {xn+yn} сходится и вещественное число a+b является ее пределом. Теорема доказана.

    Теорема 2. Произведение сходящихся последовательностей {xn} и {yn} представляет собой сходящуюся последовательность, предел которой равен произведению пределов последовательностей {xn} и {yn}.

    Теорема 3. Частное двух сходящихся последовательностей {xn} и {yn}, предел второй из которых отличен от нуля, определено, начиная с некоторого номера, и представляет собой сходящуюся последовательность, предел которой равен частному пределов последовательностей {xn} и {yn}.

    1. о пределе произведения двух последовательностей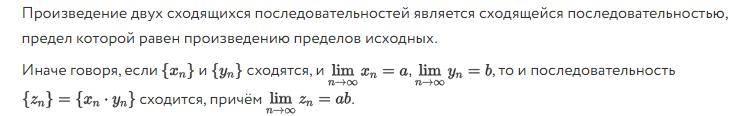



    1. о пределе частного двух последовательностей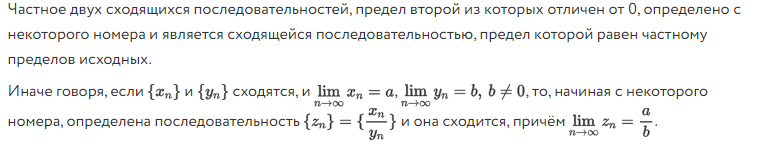



    1. об ограниченности сходящейся последовательности

    Если последовательность имеет предел, то она ограничена.

    Док-во: https://univerlib.com/mathematical_analysis/limit_sequence/definition_limit_of_sequence/

    1. о единственности предела функции

    Если существует конечный предел функции при x a  , то он единственен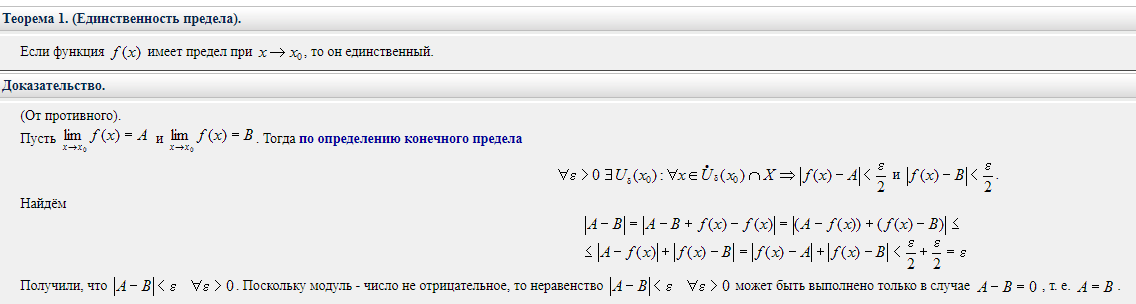



    1. о двух полицейских (для функций)



    1. основная лемма пределов

    2. о сумме двух бесконечно малых функций

    Алгебраическая сумма двух, трех и вообще любого конечного числа бесконечно малых есть функция бесконечно малая.

    Доказательство. Приведем доказательство для двух слагаемых. Пусть f(x)=α(x)+β(x), где и . Нам нужно доказать, что при произвольном как угодно малом ε>0 найдется δ>0, такое, что для x, удовлетворяющих неравенству |x – a|<δ, выполняется |f(x)|< ε.

    Итак, зафиксируем произвольное число ε>0. Так как по условию теоремы α(x) – бесконечно малая функция, то найдется такое δ1>0, что при |x – a|<δ1 имеем |α(x)|< ε/2. Аналогично, так как β(x) – бесконечно малая, то найдется такое δ2>0, что при |x – a|<δ2 имеем | β(x)|< ε/2.

    Возьмем δ=min{ δ1, δ2}.Тогда в окрестности точки a радиуса δбудет выполняться каждое из неравенств |α(x)|< ε/2 и | β(x)|< ε/2. Следовательно, в этой окрестности будет

    |f(x)|=| α(x)+β(x)| ≤ |α(x)| + | β(x)| < ε/2 + ε/2= ε,

    т.е. |f(x)|<ε, что и требовалось доказать.

    1. о произведении бесконечно малой на ограниченную функцию

    Произведение бесконечно малой функции a(x) на ограниченную функцию f(x) при x→a (или при x→∞) есть бесконечно малая функция.

    Доказательство. Так как функция f(x) ограничена, то существует число М такое, что при всех значениях x из некоторой окрестности точки a|f(x)|≤M. Кроме того, так как a(x) – бесконечно малая функция при x→a, то для произвольного ε>0 найдется окрестность точки a, в которой будет выполняться неравенство |α(x)|< ε/M. Тогда в меньшей из этих окрестностей имеем | αf|< ε/M= ε. А это и значит, что af – бесконечно малая. Для случая x→∞ доказательство проводится аналогично.

    1. о частном от деления бесконечно малой функции на функцию, имеющую конечный предел, не равный нулю



    1. о связи между бесконечно малой и бесконечной большой функциями



    1. о замене бесконечно малой функции ей эквивалентной

    Как известно, сумма, разность и произведение двух б.м.ф. есть функция бесконечно малая. Отношение же двух б.м.ф. может вести себя различным образом: быть конечным числом, быть бесконечно боль той функцией, бесконечно малой или вообще не стремиться ни к ка кому пределу. Две б.м.ф. сравниваются между собой с помощью их отношения.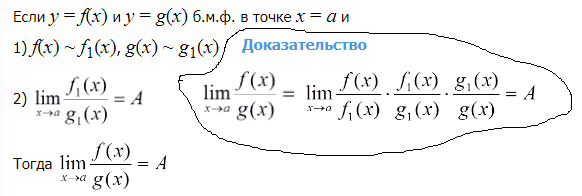



    1. о пределе суммы двух функций



    Док-во: https://1cov-edu.ru/mat-analiz/predel-funktsii/arifmeticheskie-svojstva/#summa

    1. о пределе произведения двух функций



    Док-во: https://1cov-edu.ru/mat-analiz/predel-funktsii/arifmeticheskie-svojstva/#proizvedenie

    1. о пределе частного двух функций



    Док-во: https://1cov-edu.ru/mat-analiz/predel-funktsii/arifmeticheskie-svojstva/#chastnoe

    1. о существовании предела функции



    Док-во: https://1cov-edu.ru/mat-analiz/predel-funktsii/kriterij-koshi/

    1. первый замечательный предел

     Предел отношения синуса какого-либо аргумента к этому аргументу при стремлении аргумента к нулю равен единице  и получающихся при них неопределенностей ноль делить на ноль. limα→0 (sinα/α)=1

    Док-во: https://1cov-edu.ru/mat-analiz/reshenie-predelov/dokazatelstvo-1-zamechatelnogo-predela/

    1. второй замечательный предел

    предел, на основе которого вычисляются производные показательной функции и логарифма.

    Док-во: https://1cov-edu.ru/mat-analiz/reshenie-predelov/dokazatelstvo-2-zamechatelnogo-predela/

    1. о непрерывности в точке суммы двух функций



    1. о непрерывности в точке произведения двух функций



    1. о непрерывности в точке частного двух функций



    1. о сохранении знака функции непрерывной в точке

    Пусть функция f(x) непрерывна в точке x0. И пусть она имеет положительное (отрицательное) значение в этой точке:
    f(x0) > 0     ( f(x0) < 0 ).
    Тогда существует такая окрестность U(x0) точки x0, на которой функция имеет положительное (отрицательное) значение:
    f(x) > 0     ( f(x) < 0 )  при  x ∈ U(x0).

    Док-во: https://1cov-edu.ru/mat-analiz/nepreryvnost-funktsii/v-tochke/#proof2

    1. первая теорема Вейерштрасса

    Если функция  f  непрерывна на отрезке [a,b], то она ограничена на этом отрезке.

    Док-во: https://1cov-edu.ru/mat-analiz/nepreryvnost-funktsii/na-otrezke/teoremy-vejershtrassa/#proof2

    1. вторая теорема Вейерштрасса

    Непрерывная на отрезке [a,b] функция  f  достигает на нем своих нижней и верхней граней. Или, что тоже самое, достигает на отрезке своего минимума и максимума. То есть существуют такие точки x1, x2 ∈ [a,b], так что для любого x ∈ [a,b], выполняются неравенства:
    f(x1) ≤  f(x) ≤  f(x2).

    Док-во: https://1cov-edu.ru/mat-analiz/nepreryvnost-funktsii/na-otrezke/teoremy-vejershtrassa/#proof2

    1. о вложенных отрезках

    Если имеем последовательность вложенных отрезков, то существует и притом одно единственное число  , принадлежащее всем отрезкам одновременно. (Для любой последовательности вложенных отрезков существует точка , принадлежащая всем этим отрезкам.
    Если длины отрезков стремятся к нулю: , то такая точка единственная.

    1. Больцано-Коши

    Пусть функция  f  непрерывна на отрезке [a,b]. И пусть C есть произвольное число, находящееся между значениями функции на концах отрезка: A = f(a) и B = f(b). Тогда существует точка ξ ∈ [a,b], для которой
    f(ξ) = C.

    Док-во: https://1cov-edu.ru/mat-analiz/nepreryvnost-funktsii/na-otrezke/teorema-boltsano-koshi/#proof1

    1. о существовании корня

    Если функция f(x) непрерывна на отрезке [a, b] и принимает на его концах значения разных знаков, то на этом отрезке существует, по крайней мере, один корень уравнения f(x).

    1. о непрерывности обратной функции



    Док-во:

    написать администратору сайта