силлабусс. Архитектура вычислительных систем З-О ВТ 121. Ответ a
 Скачать 49.28 Kb. Скачать 49.28 Kb.
|
| | 3 | Совокупность триггеров, связанных друг с другом определённым образом общей системой управления | 4 | *Регистр | Сумматор | Счетчик команд | Триггер | АЛУ |
| | 3 | Регистр АЛУ, участвующий в выполнении каждой операции | 4 | *Сумматор | Триггер | Счетчик команд | УУ | Процессор |
| | 3 | Регистр УУ, содержимое которого соответствует адресу очередной выполняемой команды; служит для автоматической выборки программы из последовательных ячеек памяти | 4 | *Счетчик команд | Сумматор | Триггер | АЛУ | Процессор |
| | 3 | Регистр УУ для хранения кода команды на период времени, необходимый для ее выполнения | 4 | *Регистр команд | Счетчик команд | Сумматор | Триггер | АЛУ |
| | 2 | По общей конфигурации различают | 4 | *звездообразные, шинные, кольцевые, древовидные, ячеистые локальные сети | одноранговые и на основе сервера | с маршрутизацией и селекцией информации | корпоративные и сети отделов | глобальные и локальные |
| | 2 | Локальная сеть характеризуется наличием центрального узла коммутации, к которому (или через который) посылаются все сообщения | 4 | *Звездообразная | Шинная | Кольцевая | Ячеистая | Древовидная |
| | 2 | В сетях с такой топологией все абонентские системы с помощью сетевых адаптеров подключаются к общей магистрали. Обязательным элементом является терминатор, с помощью которого устраняется эффект отраженной волны на концах коаксиального кабеля | 4 | *Шинная | Ячеистая | Древовидная | Кольцевая | Звездообразная |
| | 2 | Локальная сеть характеризуется наличием замкнутого однонаправленного канала передачи данных, в виде кольца или петли | 4 | *Кольцевая | Шинная | Звездообразная | Ячеистая | Древовидная |
| | 2 | По методам передачи информации локальные сети делятся на сети | 4 | *с маршрутизацией и селекцией информации | одноранговые и на основе сервера | глобальные и локальные | корпоративные и сети отделов | с звездообразной и шинной топологией |
| | 2 | Используется в звездообразных и древовидных локальных сетях. В отличии от глобальных сетей маршрутизация в локальных сетях имеет ограниченное количество возможных маршрутов. Ее результатом является формирование виртуальных каналов между абонентскими системами | 4 | *Маршрутизация | Селекция | Топология | Трансляция | Передача маркера |
| | 2 | Представляет собой процесс выбора очередной абонентской системы, которой предоставляется возможность передачи информации | 4 | *Селекция | Маршрутизация | Топология | Трансляция | Передача маркера |
| | 2 | Способ изображения чисел с помощью ограниченного набора символов, имеющих определенные количественные значения | 4 | *Система счисления | Топология | Трансляция | Селекция | Маршрутизация |
| | 2 | Системы счисления бывают | 4 | *Позиционные и непозиционные | Дробные и целые | Шинные, звездообразные, кольцевые | С фиксированной и с плавающей точкой | С маршрутизацией и селекцией информации |
| | 2 | В таких системах счисления каждая цифра числа имеет определенный вес, зависящий от позиции цифры в последовательности, изображающей число | 4 | *В позиционных | В непозиционных | С фиксированной точкой | С плавающей точкой | С селекцией каналов |
| | 1 | В позиционной системе счисления любое число можно представить в виде: | 4 | *An=am-1Nm-1+ am-2Nm-2+…+ a-kN-k | An=am-1Nm-1 | An=amNm+…+ akNk | An=a-1N-1+ a-2N-2+…+ a-kN-k | An=Nm-1+ Nm-2+…+ N-k |
| | 1 | В ЭВМ используются три вида чисел: | 4 | *с фиксированной точкой (запятой), с плавающей точкой (запятой) и двоично-десятичное представление | с фиксированной точкой (запятой), десятичное представление, двоичное представление | с фиксированной точкой (запятой), с плавающей точкой (запятой) и восьмеричное представление | восьмеричное представление, двоичное представление, десятичное представление | десятичное представление, с плавающей точкой, с плавающей запятой |
| | 1 | У таких чисел в двоичном формате предполагается строго определенной место точки (запятой). Обычно это место определяется или перед первой значащей цифрой числа, или после последней значащей цифры числа | 4 | *С фиксированной точкой (запятой) | С плавающей точкой (запятой) | Двоичные | Десятичные | Шестнадцатеричные |
| | 3 | Такой код двоичного числа образуется из абсолютного значения этого числа и кода знака (нуль или единица) перед его старшим разрядом | 4 | *Прямой | Обратный | Дополнительный | Модифицированный обратный код | Модифицированный дополнительный код |
| | 3 | Такой код двоичного числа образуется по следующему правилу: код положительных чисел совпадает с их прямым кодом, код отрицательного числа содержит единицу в знаковом разряде числа, а значащие разряды числа заменяются на инверсные, т.е. нули - единицами, а единицы – нулями | 4 | *Обратный | Прямой | Дополнительный | Модифицированный дополнительный | Модифицированный прямой |
| | 3 | Такой код положительных чисел совпадает с их прямым кодом, код отрицательного числа представляет собой результат суммирования обратного кода числа с единицей младшего разряда | 4 | *Дополнительный | Прямой | Обратный | Модифицированный дополнительный | Модифицированный обратный |
| | 3 | Такие коды двоичных чисел отличаются соответственно от обратных и дополнительных кодов удвоением значений знаковых разрядов. Знак "+" в этих кодах кодируется двумя нулевыми знаковыми разрядами, а знак "-" - двумя единичными разрядами | 4 | *Модифицированные обратный и дополнительный коды | Прямой и обратный | Прямой и дополнительный | Обратный и дополнительный | Модифицированные прямой и обратный коды |
| | 3 | Данная операция над двоичными числами наиболее просто реализуется в прямом коде, путем сложения частных произведений, представляющих собой разряды множимого, сдвинутые влево в соответствии с позициями разрядов множителя | 5 | *Умножение | Сложение | Вычитание | Деление | Возведение в степень |
| | 3 | Данная операция является операцией обратной умножению, и приводится к последовательности операций сложения и сдвига, осуществляется как и в десятичной системе счисления, сначала проверяется возможность вычесть значение делителя из старших разрядов делимого, если возможно, то в разряде частного записывается единица и определяется частная разница, в противном случае, в частное записывается нуль и разряды делителя сдвигаются вправо на один разряд по отношению к разрядам делимого, к полученной предыдущей разнице сносится очередная цифра делимого, и данный процесс повторяется до тех пор, пока не будет получена необходимая точность, знак частного формируется путем сложения знаковых разрядов делимого и делителя, как и при умножении | 5 | *Деление | Сложение | Вычитание | Умножение | Возведение в степень |
| | 2 | Что используется для описания логики функционирования аппаратных и программных средств ЭВМ? | 5 | *Алгебра логики | Логическая функция | Метод Квайна – МакКласки | Абстрактный автомат | Автоматы Милли и Мура |
| | 2 | Булева алгебра оперирует с логическими переменными, которые могут принимать значения: | 5 | *1 и 0 | А и В | От 1 до 9 и от A до F | Только 1 | Только 0 |
| | 2 | Основная система счисления ЭВМ, в которой используются только две цифры: 1 и 0. | 5 | *Двоичная | Двоично-десятичная | Шестнадцатеричная | Десятичная | Восьмеричная |
| | 2 | Функция от набора логических переменных (аргументов) F(х1, х2, ...,хn), которая может принимать только два значения: истина или ложь (1 или 0) | 5 | *Логическая | Каноническая | Тригонометрическая | Математическая | Универсальная |
| | 2 | С помощью нее может быть задана любая логическая функция, в левой части записываются возможные наборы аргументов, а в правой - соответствующие им значения функции | 5 | *Таблица истинности | Таблица умножения | Тригонометрическая функция | Диаграмма Вейча | Инверсия |
| | 2 | Логическую функцию порой называют… | 5 | *функцией алгебры логики (ФАЛ) | тригонометрической функцией | логическим отрицанием | инверсией | таблицей истинности |
| | 2 | Функция F2(x) называется отрицанием переменной или инверсией и обозначается так: | 5 | * 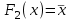 | 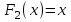 | 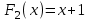 | 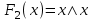 | 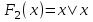 |
| | 3 | Как называется иначе логическое умножение? | 5 | *Конъюнкция | Дизъюнкция | Инверсия | Минимизация | Логическое отрицание |
| | 3 | Как называется иначе логическое сложение? | 5 | *Дизъюнкция | Конъюнкция | Инверсия | Минимизация | Логическое отрицание |
| | 3 | Отношение эквивалентности обозначается знаком | 5 | *= | + | - | Чертой над переменной | ≠ |
| | 3 | Дизъюнкция обозначается знаком | 5 | *v или символом + | ^ или символом ∙ | Чертой над переменной | ≠ | = |
| | 3 | Конъюнкция обозначается символом | 5 | *^ или символом ∙ | v или символом + | Чертой над переменной | ≠ | = |
| | 3 | Отрицание обозначается | 5 | *чертой над переменной: |
