ревр. Аттестация по матем №1. Ответ Натуральные числа
 Скачать 38.54 Kb. Скачать 38.54 Kb.
|
|
1.Определение значения натуральных, целых ,иррациональных ,рациональных, действительных чисел. ОТВЕТ: Натуральные числа-это числа , которые используются для подсчёта предметов (1,2) Целые числа- натуральные числа и им противоположные , 0 (-3, 3 ,0) Рациональные числа – числа который можно представить в виде обыкновенной дроби, то есть натуральные , целые и смешанные числа.(0,2;1,25) Иррациональные числа – это десятичные , бесконечные не переодические дроби (0,123;1,453) Действительные числа –это все рациональные и иррациональные числа (-4;100;1,2) 2.Определение комплексного числа. ОТВЕТ: Это число вида z=a+bi,где а и в это действительная часть , а для числа I справедливо равенство I ^2 =-1 3.Определение взаимосопряжённых комплексных чисел. ОТВЕТ: 2 комплексных числа называются взаимосопряженными если их действительные части равны ,а мнимые отличаются знаком ПРИМЕР: Z1=3-5И Z2=3+5И 4.Формы сложение, умножение и деление комплексных чисел. ОТВЕТ: СЛОЖЕНИЕ: Z1+Z2=(a1+a2)+(b1+b2)* I ВЫЧИТАНИЕ: Z1-Z2=(a1-a2)+(b1-b2)*I УМНОЖЕНИЕ:Z1*Z2=(a1a2-b1b2)+(  a1b2+a2b1)*I a1b2+a2b1)*IДЕЛЕНИЕ: 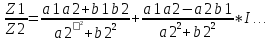 5. Решение уравнения вида x^n = a , где neN , а > 0 ОТВЕТ: Если число натуральное и а больше 0 , то уравнение имеет 2 корня X1= 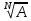 X2=- X2=-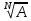 6.Определение корня n-ой степени из неотрицательного числа. ОТВЕТ :Корнем н-ой степени из неотрицательного числа а называется такое неотриц.число х, при возведении которого с степень н получается число а. 7. Определение корня не четной степени n из отрицательного числа ОТВЕТ: Корнем нечётной степени н из отрицательного числа а называется такое отрицательное число х , при возведении которого в степень получается число а. 8. Свойства корней n-ой степени Корень n-й степени из произведения двух неотрицательных чисел равен произведению корней n-й степени из этих чисел Корень частного равен частному корней Чтобы возвести корень в натуральную степень, достаточно возвести в эту степень подкоренное выражение Чтобы извлечь корень из корня, достаточно перемножить показатели корней Если показатели корня и подкоренного выражения умножить или разделить на одно и то же число, то значение корня не изменится 9. Определение степени с положительный рациональным показателем ОТВЕТ: Если 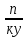 – обыкновенная дробь , ку ≠ 1 , а ≥ 0 то под выражением а^ – обыкновенная дробь , ку ≠ 1 , а ≥ 0 то под выражением а^ 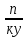 понимают понимают 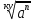 (корень ку из а в степени п) 10. Определение степени с отрицательным рациональным показателем ОТВЕТ: Если 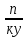 обыкновенная дробь , ку ≠ 1 , а >0 под выражением a^ обыкновенная дробь , ку ≠ 1 , а >0 под выражением a^ 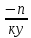 Понимают 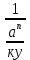 11. Свойства степени с рациональным показателем . 1. При умножении степеней с одинаковыми основаниями показатели степеней складываются 2. Когда мы делим степени с одинаковыми основаниями, основание остается без изменений, а из показателя степени делимого вычитают показатель степени делителя 3. Если необходимо возвести одну степень в другую, основанием останется то же число, а показатели степени перемножаются. 4. При возведении в степень произведения возводят в эту степень каждый множетель и результаты перемножают 5. При возведении в степень дроби возводят в эту степень числитель и знаменатель дроби 12.Определение логарифма, десятичного и натурального логарифма. ОТВЕТ: Логарифмом положительного числа b положительному числу а и не равному 1 основанию а называется показатель степени, в которую надо возвести число а, чтобы получить число b Десятичный логарифм-это логарифм положительного числа по основанию 10 Натуральный логарифм-логарифм полож.числа по основанию е |
