Матан ответы. МатАн. ОТВЕТЫ 2017. Свойства
 Скачать 22.33 Kb. Скачать 22.33 Kb.
|
|
Модуль действительного числа и его свойства. Модуль числа – абсолютная положительная величина числа. Свойства |a|=|-a| |a 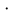 b|=|a| b|=|a|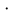 |b| |b|Модуль частного от деления a на b равен частному от деления модуля числаaна модуль числаb, то есть, 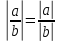 Модуль суммы двух чисел меньше суммы модулей этих чисел. |a+b|  |a|+|b| |a|+|b|Предел числовой последовательности. Число A 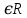 называется пределом числовой последовательности называется пределом числовой последовательности 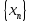 , если , если 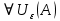 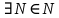 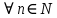  Пишут: 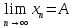 Предел функции, теорема единственности предела. (Коши) Число 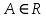 называется пределом функции называется пределом функции 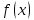 в точке в точке  , если: , если:Функция 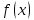 определена в некоторой проколотой окрестности точки определена в некоторой проколотой окрестности точки 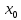 выполняется условие: 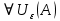 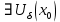 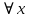 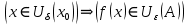 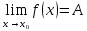 (Гейне) Число 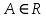 называется пределом функции называется пределом функции 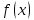 в точке в точке  , если: , если:Функция 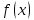 определена в некоторой проколотой окрестности точки определена в некоторой проколотой окрестности точки 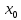 Для любой последовательности точек 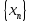 из некоторой проколотой окрестности точки из некоторой проколотой окрестности точки 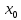 , имеющей своим пределом , имеющей своим пределом 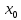 , соответствующая последовательность значений функции , соответствующая последовательность значений функции 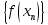 имеет своим пределом число А имеет своим пределом число АЕсли функция имеет предел в точке, то этот предел единственный. Ограниченность функции, имеющей конечный предел. Если функция имеет конечный предел в точке, то она ограничена в некоторой проколотой окрестности этой точки. Предел суммы, произведения и частного функций. Предел суммы 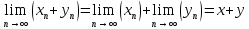 Предел произведения 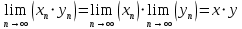 Пределчастного 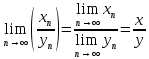 Предельный переход в неравенствах. Пусть в некоторой проколотой окрестности точки 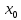 выполняется неравенство выполняется неравенствоf(x)  g(x) . Тогда g(x) . Тогда 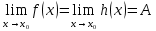 , если пределы существуют. , если пределы существуют.Свойства бесконечно больших и бесконечно малых величин. Сравнение бесконечно малых. Функция  называется бесконечно малой при называется бесконечно малой при 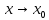 если если 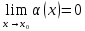 Функция 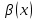 называется бесконечно большой при называется бесконечно большой при 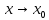 если если 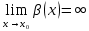 Свойства Произведение бесконечно малой при 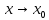 на функцию, ограниченную в некоторой проколотой окрестности точки на функцию, ограниченную в некоторой проколотой окрестности точки 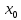 , является бесконечно малой при , является бесконечно малой при 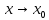 Если  – бесконечно малая при – бесконечно малая при 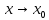 , не принимающая значение 0 в некоторой проколотой окрестности точки , не принимающая значение 0 в некоторой проколотой окрестности точки 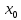 , то , то 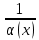 – бесконечно большая при – бесконечно большая при 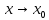 Если 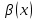 – бесконечно большая при – бесконечно большая при 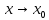 , не принимающая значение 0 в некоторой проколотой окрестности точки , не принимающая значение 0 в некоторой проколотой окрестности точки 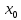 , то , то 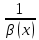 – бесконечно малая при – бесконечно малая при 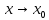 Функция  является бесконечно малой более высокого порядка по сравнению с является бесконечно малой более высокого порядка по сравнению с 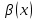 при при 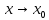 , если , если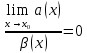 Непрерывность основных элементарных и элементарных функций. Классификация точек разрыва. основные элементарные функции: степенные функции 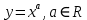 показательные функции 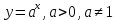 логарифмические функции 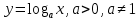 тригонометрические функции 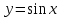  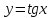 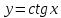 круговые (обратные тригонометрические) функции  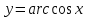 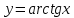 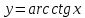 Функция называется элементарной, если она может быть представлена через основные элементарные функции с помощью конечного числа операций Основные элементарные функции непрерывны в области определения. Точка, в которой функция не является непрерывной, называется точкой разрыва. 1) Функция f (x) имеет в точкеxoустранимый разрыв, если выполняются условия 1–2, но не выполняется условие 3. Точкааназывается точкой устранимого разрыва функции, если предел функции в этой точке существует, но в точке а функция либо не определена, либо ее значение не равно пределу в этой точке 2) Функция f (x) имеет в точкеxoразрыв I рода («разрыв скачка»), если выполняется только условие 1. Точка а называется точкой разрыва первого рода функции, если в этой точке функция имеет конечные, но не равные друг другу левый и правый пределы. 3) Функция f (x) имеет в точкеxoразрыв II рода, если условие 1 не выполняется. Точка а называется точкой разрыва второго рода функции. Точка а называется точкой устранимого разрыва функции, если в этой точке функция не имеет по крайней мере одного из односторонних пределов или хотя бы один из односторонних пределов бесконечен. Теорема Коши о промежуточных значениях функции, непрерывной на отрезке. Если функция f (x) непрерывна на промежутке X и её значения f(a)=A, f(b)=B, то для любого числа C, заключённого между A и B, существует точка x0 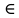 X, в которой значение f(x0)=C X, в которой значение f(x0)=CТеорема Вейерштрасса об ограниченности функции, непрерывной на отрезке. Если функция непрерывна на отрезке, то она ограничена на нём. Теорема Вейерштрасса о достижении наибольшего и наименьшего значений функции, непрерывной на отрезке. Если функция непрерывна на отрезке, то среди её значений на этом отрезке есть наибольшее и наименьшее Производная и дифференциал, дифференцирование функций. Производная — основное понятие дифференциального исчисления, характеризующее скорость изменения функции. Определяется как предел отношения приращения функции к приращению её аргумента. дифференциал функции y = f(x) в точке x равен приращению ординаты касательной к графику функции в этой точке, когда x получит приращение 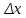 . .Дифференцирование произведения функций. 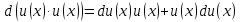 Дифференцирование сложной функции. 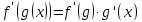 Связь непрерывности и дифференцируемости функции. Если функция y=f(x) дифференцируема на некотором интервале, то она и непрерывна на этом интервале. Но обратное утверждение НЕВЕРНО. |
