ответы. основы энергетики. Ответы к экзаменационным вопросам по предмету Основы энергетики
 Скачать 0.74 Mb. Скачать 0.74 Mb.
|
|
2) концы стержня находятся в той же теплоизолирующей оболочке, что и весьстержень. Это означает, что через концы не происходит протекание тепла. Рассмотрим сечение х нашего стержня и найдем, какое количество Q тепла протечет (слева направо) через это сечение за элементарный промежуток времени где k – коэффициент теплопроводности ( Составим тепловой баланс для элемента Тогда через сечение с абсциссой х тепло выходит, а через сечение с абсциссой x + dx входит. Пусть dQ есть количество тепла, накопленное нашим элементом Используя формулу (4.37) будем иметь: 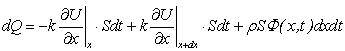 . (4.39) . (4.39)Применяя формулу Лагранжа из дифференциального исчисления 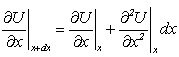 . .Следовательно, формула (4.39) примет вид: С другой стороны, Итак, сравнивая (4.41) и (4.40), после сокращения получим: или, обозначая Если источники тепла отсутствуют, то уравнение (4.43) принимает вид уравнения свободного теплообмена в стержне: Аналогичным образом можно вывести уравнения для распространения температуры в пластине: 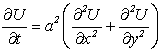 ; ;и в тепле 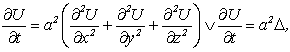 где Вывод: уравнение теплопроводности есть уравнение с частными производными второго порядка, параболического типа, так как 1) Найти то решение уравнения (4.44), которое удовлетворяет начальному условию (4.35) и граничным условиям (4.36). 2) Найти то решение уравнения (4.44), которое удовлетворяет начальному условию (4.35) и граничным условиям: 7. Начальные условия и граничные условия - условия однозадачности Дифференциальное уравнение теплопроводности описывает явление в самом общем виде, т.е. описывает классявлений теплопроводности. Чтобы рассмотреть данный конкретный процесс следует дать дополнительное математическое описание конкретного процесса теплопроводности, называемое условиями однозначности(единственности), которые включают в себя: 1) геометрическую форму и размеры тела, в котором протекает процесс; 2) граничные условия, характеризующие физическую связь тела с окружающей средой; 3) начальные условия, распределения температур в начальный момент времени и условия протекания процесса во времени; 4) физические свойства тела и окружающей среды, определяемые физическими параметрами; 5) интенсивность и распределение внутренних источников тепла. Совокупность начальных и граничных условий называют краевыми условиями. Начальные условия при нагреве (или охлаждении) тела сказываются только в начальный период, но по истечении некоторого времени наступает регулярный режим, при котором распределение температур в теле определяется только граничными условиями и не зависит от начальных. Граничные условия задаются соответственно способу нагрева (охлаждения), т.е. воздействию окружающей среды на тело. 1.Если задается изменение температуры на поверхности тела во времени tпов= f( 2.Если на поверхности тела задана плотность теплового потока, то мы имеем граничные условия второго рода. По закону Фурье Градиент температуры относится к точке тела, расположенной в непосредственной близости от поверхности тела (х= +0). 3.Граничные условия третьего рода соответствуют случаю конвективного теплообмена с поверхностью тела (конвективной теплоотдаче). Тепловой баланс на границе тела имеет вид Этот случай часто применяют при решении практических задач. 4. В высокотемпературных печах чаще всего передача тепла осуществляется лучеиспусканием. Тогда тепловой баланс на границе может быть описан уравнением Если разность температур среды и поверхности невелика и соблюдается неравенство 0,9 <Токр/Тх=0<1,1, то этот случай можно свести к граничным условиям 3-го рода и тогда где Различают два режима распространения тепла в теле: а) при установившемся (стационарном) режиме, когда температурное поле тела не изменяется во времени, т. е. когда температура каждой точки постоянна ( 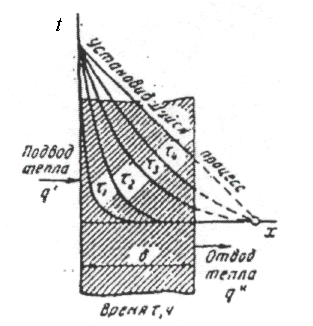 Рис.1.4. Процессы прогрева плоской стенки (пластины). Кривые показывают распределение температур по истечении времени 8. Стационарные одномерные стационарные задачи теплопроводности Применим уравнение теплопроводности для решения задач, в которых температура зависит только от одной линейной координаты. Примем, что в прямоугольной системе координат температура будет зависеть только от x, а в цилиндрической и сферической системах координат—только от радиуса. Предполагается, что коэффициент теплопроводности является постоянной величиной, а тепловыделение отсутствует. Применим общую методику решения, состоящую из двух этапов. На первом этапе из решения соответствующего упрощенного уравнения теплопроводности находится распределение температуры. С этой целью отыскивается аналитическое решение дифференциального уравнения второго порядка. После того как решение дифференциального уравнения записано в общем виде, с помощью двух граничных условий определяются две постоянные интегрирования. На втором этапе с помощью закона Фурье вычисляется кондуктивный тепловой поток через твердое тело. 1.1 Общее понятие термического сопротивления Математическое выражение закона Гука имеет вид: или после разделения переменных интегрируя в пределах изменения пространственной координаты и в соответствующем температурном интервале, получаем 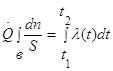 или или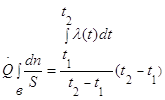 Выражение 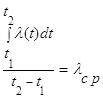 называется среднеинтегральным коэффициентом теплопроводности в интервале При постоянном: Таким образом, имеем 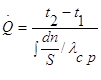 Сравнивая полученное уравнение с выражением закона Ома получаем уравнение, определяющее термическое сопротивление теплопроводности в общем случае 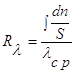 (1.0) (1.0)Для получения выражения, определяющего термическое сопротивление конвективного теплообмена, рассмотрим закон Ньютона-Рихмана 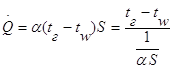 То есть термическое сопротивление конвективного теплообмена определится выражением 1.2 Прямоугольные координаты Стационарное одномерное распределение температуры в плоской прямоугольной стенке при отсутствии внутреннего тепловыделения описывается упрощенным уравнением теплопроводности d2T/dx2 = 0. Решение этого дифференциального уравнения с использованием двух постоянных интегрирования C1 и С2 имеет вид: Т (х) = С1x + С2. Значения этих постоянных можно найти, если заданы два граничных условия. Предположим, что в качестве этих условий заданы температуры на двух поверхностях стенки (рисунке 1.1): Т(0)=T1 и T(b)=T2. Применяя эти граничные условия, получаем следующее распределение безразмерной температуры в стенке: 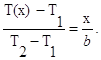 (1.1) (1.1)Следовательно, температура изменяется линейно по x. Тепловой поток через стенку определяется законом Фурье: Тепловой поток на единицу площади называется плотностью теплового потока и обозначается q. Для плоской стенки 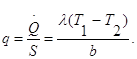 Если записать соотношение (1.2) в форме закона Ома: 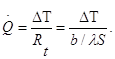 (1.3) (1.3)то термическое сопротивление плоской стенки выражается формулой Используя общее понятие термического сопротивления теплопроводности, (1.0), получаем аналогичное выражение 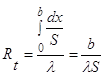 Кондуктивный тепловой поток через плоскую стенку обусловлен перепадом температур поперек стенки, и его распространению противодействует термическое сопротивление, пропорциональное толщине стенки и обратно пропорциональное коэффициенту теплопроводности стенки и площади ее поперечного сечения. Если кондуктивный перенос тепла осуществляется через составную (многослойную) плоскую стенку, распределение температуры и тепловой поток можно найти, предполагая, что тепло течет по эквивалентной тепловой цепи, представляющей сумму термических сопротивлений, соответствующих отдельным слоям из различных материалов. В качестве примера тепловой цепи рассмотрим плоскую стенку (индекс 1), покрытую двумя слоями различных изоляционных материалов (индексы 2 и 3). Геометрия задачи показана на рисунке 1.2. Один и тот же тепловой поток проходит последовательно через каждое термическое сопротивление, и, следовательно, тепловая цепь состоит из последовательно соединенных термических сопротивлений. Если известны свойства всех трех материалов, заданы геометрические характеристики и температуры на двух внешних поверхностях, тепловой поток можно найти с помощью соотношения, аналогичного закону Ома: 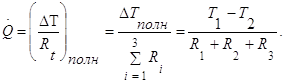 (1.5) (1.5)Поскольку тепловой поток через многослойную стенку известен, можно найти температуры на поверхностях раздела материалов, применяя закон Ома для каждого слоя. Например, температуру Тx на поверхности раздела материалов 1 и 2 можно рассчитать по формуле 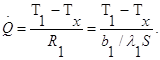 (1.6) (1.6)Часто в многослойных стенках слои материалов расположены так, что тепловой поток через них течет скорее параллельно, чем последовательно. В таком случае в тепловую цепь включаются участки из параллельно соединенных термических сопротивлений. Тепловой поток определяется по формуле 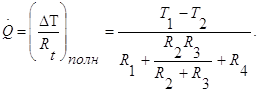 (1.7) (1.7)Отдельные термические сопротивления выражаются соотношением 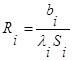 . . Промежуточные температуры типа ТX можно найти из уравнения (1.6). Предполагается, что при параллельном соединении термических сопротивлений R2 и R3 тепловой поток остается одномерным; если же сопротивления R2 и R3 заметно отличаются друг от друга, могут стать существенными двумерные эффекты. 9. Теплопроводность цилиндрической стенки Граничные условия первого рода. Рассмотрим стационарный процесс теплопроводности в цилиндрической стенке (трубе) с внутренним диаметром d1=2r1 и наружным диаметром d2=2r2 (рис.2.6). На поверхностях стенки заданы постоянные температуры tc1 и tc2. В заданном интервале температур коэффициент теплопроводности материала стенки λ является постоянной величиной. Необходимо найти распределение температур в цилиндрической стенке и тепловой поток через нее. 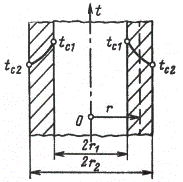 Рис. 2.6. Теплопроводность цилиндрической стенки. В рассматриваемом случае дифференциальное уравнение теплопроводности удобно записать в цилиндрической системе координат: 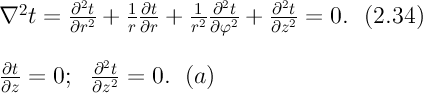 Кроме того, так как температуры на наружной и внутренней поверхностях трубы неизменны, изотермические поверхности являются цилиндрическими, имеющими с трубой общую ось. Тогда температура не должна изменяться также вдоль φ, т. е. Кроме того, так как температуры на наружной и внутренней поверхностях трубы неизменны, изотермические поверхности являются цилиндрическими, имеющими с трубой общую ось. Тогда температура не должна изменяться также вдоль φ, т. е.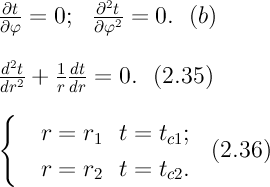 В виде (2.35) можно записать уравнение (2.34) с учётом (a) и (b). (2.36) - граничные условия для (2.35). Если решить уравнение (2.35) совместно с (2.36), получим уравнение температурного поля в цилиндрической стенке. Введем новую переменную В виде (2.35) можно записать уравнение (2.34) с учётом (a) и (b). (2.36) - граничные условия для (2.35). Если решить уравнение (2.35) совместно с (2.36), получим уравнение температурного поля в цилиндрической стенке. Введем новую переменную 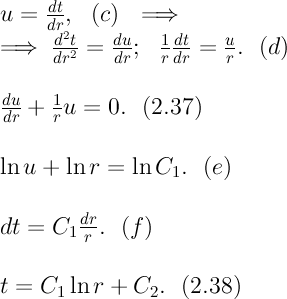 Выражение (2.37) получается, если в уравнение (2.35) подставить выражения (c) и (d). Проинтегрировав (2.37), получаем выражение (е). Потенцируя выражения (е) и переходя к первоначальным переменным, получаем (f). Выражение (2.38) получается в результате интегрирования (f). Постоянные С1 и С2можно определить, если в уравнение (2.38) подставить граничные условия: Выражение (2.37) получается, если в уравнение (2.35) подставить выражения (c) и (d). Проинтегрировав (2.37), получаем выражение (е). Потенцируя выражения (е) и переходя к первоначальным переменным, получаем (f). Выражение (2.38) получается в результате интегрирования (f). Постоянные С1 и С2можно определить, если в уравнение (2.38) подставить граничные условия: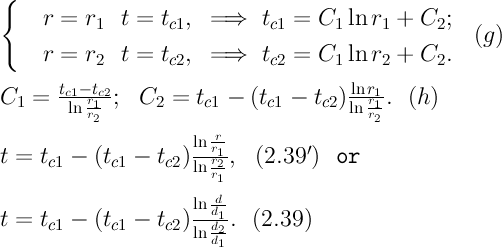 Решение уравнений (g) относительноС1 и С2 дает (h). Подставив (h) (значения С1 и С2 ) в уравнение (2.38), получим (2.39') или (2.39). Полученное выражение представляет собой уравнение логарифмической кривой. То обстоятельство, что распределение температуры в цилиндрической стенке является криволинейным, можно объяснить следующим. Для плоской стенки плотность теплового потока qостается одинаковой для всех изотермических поверхностей. По этой причине градиент температуры сохраняет для всех изотермических поверхностей постоянное значение. Для цилиндрической стенки плотность теплового потока через любую изотермическую поверхность зависит от радиуса. Для нахождения количества теплоты, проходящего через цилиндрическую поверхность площадью F в единицу времени, можно воспользоваться законом Фурье: Решение уравнений (g) относительноС1 и С2 дает (h). Подставив (h) (значения С1 и С2 ) в уравнение (2.38), получим (2.39') или (2.39). Полученное выражение представляет собой уравнение логарифмической кривой. То обстоятельство, что распределение температуры в цилиндрической стенке является криволинейным, можно объяснить следующим. Для плоской стенки плотность теплового потока qостается одинаковой для всех изотермических поверхностей. По этой причине градиент температуры сохраняет для всех изотермических поверхностей постоянное значение. Для цилиндрической стенки плотность теплового потока через любую изотермическую поверхность зависит от радиуса. Для нахождения количества теплоты, проходящего через цилиндрическую поверхность площадью F в единицу времени, можно воспользоваться законом Фурье: 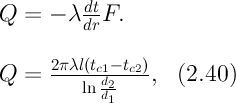 Подставляя в уравнение закона Фурье значение градиента температуры согласно уравнению (f), получаем (учитывая, что F=2 Подставляя в уравнение закона Фурье значение градиента температуры согласно уравнению (f), получаем (учитывая, что F=2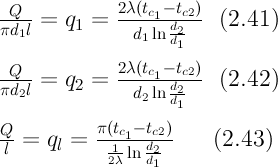 (2.41) - тепловой поток через единицу внутренней поверхности; (2.42) - тепловой поток через единицу наружной поверхности; (2.43) - поток теплоты, проходящий через единицу длины трубы, Вт/м. Тепловой поток, отнесенный к единице длины трубы, измеряется в Вт/м и называется линейной плотностью теплового потока. Как видно из уравнения (2.43), при неизменном отношении линейная плотность теплового потока не зависит от поверхности цилиндрической стенки. Плотности теплового потокаq1и q2 (отнесенные к внутренней и внешней поверхности) при передаче теплоты через трубы неодинаковы, причем всегда q1>q2. Последнее ясно видно из уравнений (2.41) и (2.42). Из уравнений (2.41)—(2.43) легко установить связь между величинами q1, q2 и ql: (2.41) - тепловой поток через единицу внутренней поверхности; (2.42) - тепловой поток через единицу наружной поверхности; (2.43) - поток теплоты, проходящий через единицу длины трубы, Вт/м. Тепловой поток, отнесенный к единице длины трубы, измеряется в Вт/м и называется линейной плотностью теплового потока. Как видно из уравнения (2.43), при неизменном отношении линейная плотность теплового потока не зависит от поверхности цилиндрической стенки. Плотности теплового потокаq1и q2 (отнесенные к внутренней и внешней поверхности) при передаче теплоты через трубы неодинаковы, причем всегда q1>q2. Последнее ясно видно из уравнений (2.41) и (2.42). Из уравнений (2.41)—(2.43) легко установить связь между величинами q1, q2 и ql: 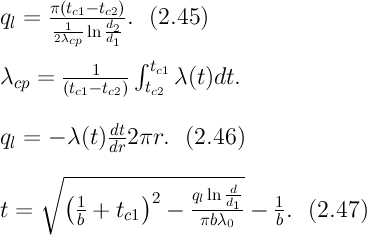 λcp – среднеинтегральное значение коэффициента теплопроводности. Для нахождения температурного поля при λ=λ(t)=λ0(1+bt) можно воспользоваться уравнением закона Фурье, записанного для цилиндрической стенки - выражение (2.46). Если разделить переменные и проинтегрировать уравнение (2.46) в пределах от r=r1до r и от t=tc1 до t и найти из полученного интеграла t, то получим выражение для температурного поля - выражение (2.47). λcp – среднеинтегральное значение коэффициента теплопроводности. Для нахождения температурного поля при λ=λ(t)=λ0(1+bt) можно воспользоваться уравнением закона Фурье, записанного для цилиндрической стенки - выражение (2.46). Если разделить переменные и проинтегрировать уравнение (2.46) в пределах от r=r1до r и от t=tc1 до t и найти из полученного интеграла t, то получим выражение для температурного поля - выражение (2.47).Граничные условия третьего рода (теплопередача). Рассмотрим однородную цилиндрическую стенку (трубу) с постоянным коэффициентом теплопроводности λ. Заданы постоянные температуры подвижных сред tF1 и tF2 и постоянные значения коэффициентов теплоотдачи на внутренней и наружной поверхностях трубы 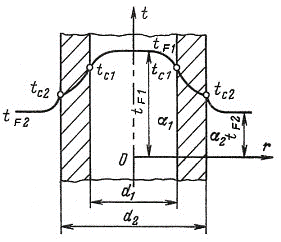 Рис. 2.7. Теплопередача через однородную цилиндрическую стенку. Необходимо найти ql и tc. Будем полагать, что длина трубы велика по сравнению с толщиной стенки. Тогда потерями теплоты с торцов трубы можно пренебречь, и при установившемся тепловом режиме будет проходить через стенку и отдаваться от стенки к холодной жидкости одно и то же количество теплоты. Следовательно, можно написать: 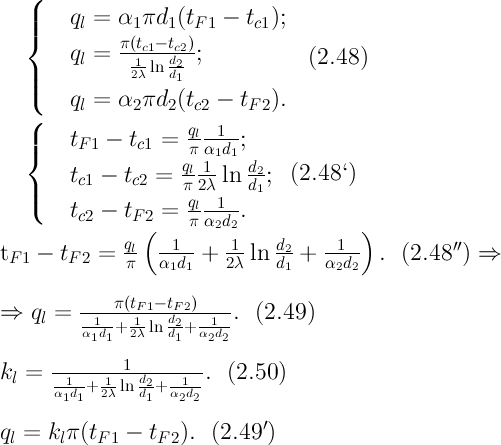 Выражение (2.49) получается из (2.48''). Температурный напор (2.48'') находим в результате сложения уравнений системы (2.48'). Выражения (2.48') получены из (2.48). Величинаkl называется линейным коэффициентом теплопередачи и измеряется в Вт/(м×К). Она характеризует интенсивность передачи теплоты от одной среды к другой через разделяющую их стенку. Значение kl численно равно количеству теплоты, которое проходит через стенку длиной 1м в единицу времени от одной среды к другой при разности температур между ними 1К. Величина Rl=1/kl ,м×К/Вт, обратная линейному коэффициенту теплопередачи, называется линейным термическим сопротивлением теплопередачи. Она равна: Выражение (2.49) получается из (2.48''). Температурный напор (2.48'') находим в результате сложения уравнений системы (2.48'). Выражения (2.48') получены из (2.48). Величинаkl называется линейным коэффициентом теплопередачи и измеряется в Вт/(м×К). Она характеризует интенсивность передачи теплоты от одной среды к другой через разделяющую их стенку. Значение kl численно равно количеству теплоты, которое проходит через стенку длиной 1м в единицу времени от одной среды к другой при разности температур между ними 1К. Величина Rl=1/kl ,м×К/Вт, обратная линейному коэффициенту теплопередачи, называется линейным термическим сопротивлением теплопередачи. Она равна: 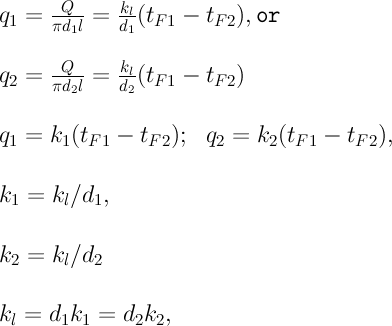 гдеklизмеряется в Вт/(м×К). Последнее соотношение устанавливает связь между коэффициентом теплопередачи при отнесении теплового потока к единице длины цилиндрической стенки и к единице поверхности. Формулы же для k1 и k2,Вт/(м2×К), в развернутом виде имеют вид: гдеklизмеряется в Вт/(м×К). Последнее соотношение устанавливает связь между коэффициентом теплопередачи при отнесении теплового потока к единице длины цилиндрической стенки и к единице поверхности. Формулы же для k1 и k2,Вт/(м2×К), в развернутом виде имеют вид: 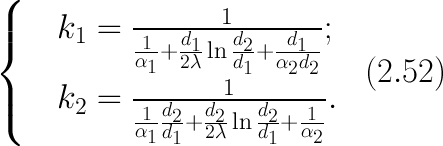 На практике часто встречаются цилиндры, толщина стенок которых мала по сравнению с диаметром. В этом случае при расчетах можно пользоваться упрощенными формулами. Для получения таких формул поступим следующим образом. Величину На практике часто встречаются цилиндры, толщина стенок которых мала по сравнению с диаметром. В этом случае при расчетах можно пользоваться упрощенными формулами. Для получения таких формул поступим следующим образом. Величину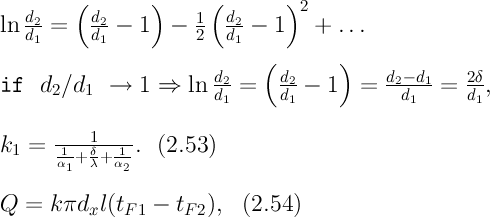 Если отношениеd2/d1→1, то такой ряд быстро сходится, и с достаточной точностью можно ограничиться первым членом ряда (где δ - толщина цилиндрической стенки, м). Подставив, полученное значение Если отношениеd2/d1→1, то такой ряд быстро сходится, и с достаточной точностью можно ограничиться первым членом ряда (где δ - толщина цилиндрической стенки, м). Подставив, полученное значение 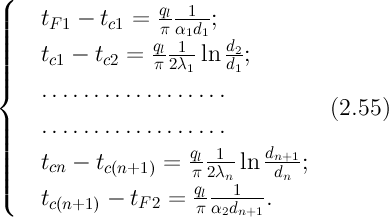 После сложения равенств (2.55) и решения относительноql , Вт/м, получим: После сложения равенств (2.55) и решения относительноql , Вт/м, получим: 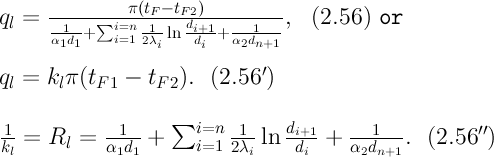 Величина (2.56'') называется полным термическим сопротивлением многослойной цилиндрической стенки и измеряется в м×К/Вт. Из уравнения (2.55) следует, что Величина (2.56'') называется полным термическим сопротивлением многослойной цилиндрической стенки и измеряется в м×К/Вт. Из уравнения (2.55) следует, что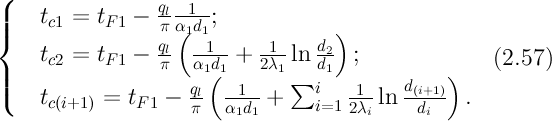 При задании граничных условий первого рода их можно рассматривать как предельный случай граничных условий третьего рода, когда коэффициенты теплоотдачи на поверхностях При задании граничных условий первого рода их можно рассматривать как предельный случай граничных условий третьего рода, когда коэффициенты теплоотдачи на поверхностях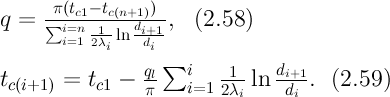 (2.59) - выражение для расчета температуры на границах между слоями. (2.59) - выражение для расчета температуры на границах между слоями.10. Теплопроводность при нестационарном режиме Процессы передачи теплоты, в которых температурное поле и поле теплового потока изменяются во времени, называются нестационарными. Нестационарные тепловые процессы в технике и природе встречаются практически чаще, чем стационарные. Нагрев или охлаждение приборов и машин при пуске, останове или изменении режима; конструктивных элементов зданий и других сооружений при изменении наружной температуры; термическая обработка продуктов и изделий; работа регенеративных теплообменных аппаратов – все это примеры нестационарных тепловых процессов. Длительность процессов нестационарного конвективного теплообмена и излучения сравнительно мала и не имеет существенного влияния на формирование температурных полей тел в нестационарном режиме, поэтому эти процессы пока мало изучены – их нестационарностью обычно пренебрегают. Процессы же теплопроводности, наоборот, оказывают решающее влияние на формирование температурных полей при нестационарном тепловом состоянии отдельных тел и систем. Процессы нестационарной теплопроводности можно разделить на две группы: а) нестационарные процессы, связанные с нарушением теплового равновесия, когда с течением времени система стремится к некоторому новому равновесному состоянию; б) нестационарные процессы, связанные с периодическим изменением теплового состояния тела (периодические изменения температуры окружающей среды или мощности тепловых источников и т. п.). В большинстве задач нестационарной теплопроводности требуется найти температуры в определенных точках тела в заданный момент времени t от начала процесса. Возможна и обратная задача: найти длительность процесса, в результате которого температура в данной точке тела примет определенное, наперед заданное значение. В некоторых задачах бывает необходимо найти тепловой поток в определенной точке в заданный момент времени или полное количество теплоты, отданной (или полученной) телом в течение заданного промежутка времени. Все перечисленные задачи сводятся к нахождению температуры рассматриваемого тела как функции времени и координат t = f(t, x, у, z). Эту зависимость можно найти, если проинтегрировать дифференциальное уравнение теплопроводности при заданных краевых условиях. Для некоторых конкретных задач теплопроводности дифференциальное уравнение может быть упрощено: в случае передачи теплоты в одном направлении задача становится одномерной; при распространении теплоты в двух направлениях задача является двухмерной. Для тел цилиндрической формы удобно перейти к цилиндрическим координатам, а для тел шаровой формы – к сферическим. Дифференциальное уравнение и краевые условия полностью формулируют задачу. Дальнейшее аналитическое ее решение сводится к использованию методов математической физики. Основные из них: метод разделения переменных, методы интегральных преобразований (например, Лапласа), метод мгновенных точечных источников. Кроме аналитических применяют и приближенные методы. Будем рассматривать задачу теплопроводности при постоянных значениях теплофизических характеристик тела (l, с,r) с граничными условиями третьего рода, так как они наиболее часто встречаются на практике. Задача формулируется следующим образом. Плоская неограниченная пластина толщиной d, имеющая во всех точках одинаковую начальную температуру tнч, в момент времени t = 0 помещается в среду, температура которой tж < tнч. Температура среды во время охлаждения поддерживается постоянной. Охлаждение пластины происходит через обе ее поверхности с одинаковой интенсивностью путем теплоотдачи, т.е., тепловой поток на поверхности подчиняется закону Ньютона-Рихмана q = a(tc – tж). Коэффициент теплоотдачи a известен и не меняется в течение всего процесса. Известен также материал, из которого выполнена пластина. Требуется найти температурное поле пластины в произвольный момент времени t > 0. Математически задачу можно сформулировать следующим образом. Дифференциальное уравнение теплопроводности для одномерной задачи без внутренних источников теплоты 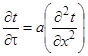 , ,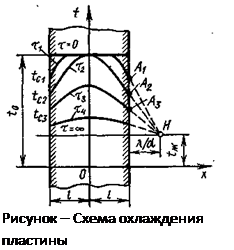 где х может изменяться в пределах 0 £ х £ d/2: так как охлаждение пластины происходит симметрично, целесообразно поместить начало координат в середину пластины и рассматривать процесс только в одной ее половине (см. рисунок). Краевые условия: где х может изменяться в пределах 0 £ х £ d/2: так как охлаждение пластины происходит симметрично, целесообразно поместить начало координат в середину пластины и рассматривать процесс только в одной ее половине (см. рисунок). Краевые условия:1) начальное условие при t = 0 и 0 £ х £ d/2 t = tнч; 2) граничные условия: а) при х = 0и t > 0 (дt/дx)0 = 0, т. к. при симметричном охлаждении в середине пластины в любой момент времени температура будет максимальной; б) при х = l и t > 0 -l(дt/дx)c = a(tc – tж). Последнее выражение записано на основании равенства тепловых потоков на поверхности пластины: подходящего к поверхности из внутренних областей тела путем теплопроводности и отводимого от поверхности в процессе теплоотдачи. Решение задачи в общем виде можно представить как функцию независимых переменных х и t и параметров процесса а,l, a, l, tж, tнч: t = f(х,t, а,l, a, l, tж, tнч). Следуя методу подобия, приведем условия задачи к безразмерной форме; это значительно сокращает число переменных, придает полученному решению обобщенность, и упрощает анализ решения. Для этого произведем сначала замену искомой величины t так называемой избыточной температурой J = t – tж. Так как dJ = dt,то запись дифференциального уравнения и граничных условий от такой замены не изменится: 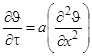 ; ;при t = 0 и 0 £ х £ l J = Jнч где Jнч = tнч – tж; при х = 0, t > 0 (дJ/дx)0 = 0; при х = l и t > 0 (дJ/дx)c = -(a/l)Jс, где Jс = tс – tж. Приведем уравнение и граничные условия к безразмерному виду. Для этого еще раз произведем замену переменных: вместо избыточной температуры введем безразмерную избыточную температуру Q = J/Jнч.Вместо координаты х введем безразмерную координату Х = х/l.Такая замена равносильна тому, что в качестве масштаба для измерения температуры используется величина Jнч, а в качестве масштаба длины – величина l. Для сохранения равенств исходные уравнения в соответствующих местах необходимо умножить на масштабы температуры и длины. Тогда дифференциальное уравнение будет иметь вид: 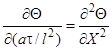 . .В такой форме дифференциальное уравнение безразмерно: величина l2/а имеет размерность времени и потому комплекс аt/l2безразмерен. Этот комплекс обозначается символом Fo и называется критерием Фурье: Fo = at/l2. Критерий Фурье можно трактовать как безразмерное время. Окончательно дифференциальное уравнение теплопроводности в безразмерной записи получается в следующем виде: Начальное условие: при Fo = 0, Qнч = 1; граничные условия: при Х = 0 (дQ/дХ)0 = 0; при X = l (дQ/дХ)с = Bi×Qc, где Qс = Jс/Jнч – безразмерная температура поверхности стенки; Bi = al/l – критерий Био. Физический смысл критерия Био в том, что его величина характеризует соотношение интенсивностей отвода теплоты в процессе теплоотдачи и подвода теплоты из внутренних слоев тела к поверхности в результате теплопроводности. Теперь искомая функция будет иметь вид Q = f(Fo,Bi, X). Применяя метод разделения переменных решение дифференциального уравнения будет иметь вид 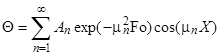 , (1) , (1)где mп – корни характеристического уравнения m/Bi = ctgm. Значения mп и Ап приводятся в справочниках. Результирующее выражение температурной функции, в форме произведения функции времени exp(-m2Fo) на некоторую функцию от координаты справедливо не только для пластины, но и для других тел, в которых распространение теплоты происходит в одном направлении, как, например, в бесконечно длинном цилиндре или шаре. Различаются результирующие выражения видом функции координаты: вместо cos – для пластины, для цилиндра появляется функция Бесселя, а для шара – гиперболическая. Для классических тел получены аналитические решения задач нестационарной теплопроводности. В соответствии с формой результирующих уравнений (1) порядок решения задачи нестационарной теплопроводности для тела классической формы следующий: 1. На основании исходных данных вычисляют безразмерную координату Х и критерии Bi и Fo. Здесь характерный размер тела: для пластины при симметричном охлаждении l = d/2,при одностороннем охлаждении l = d;для бесконечно длинного цилиндра и шара l = R,где R – радиус. 2. По величине критерия Bi в специальных таблицах находят значения mnи Апдля нескольких значений п.В обычных инженерных расчетах достаточно учитывать два-четыре члена суммы в формуле (1). 3. По формуле (1) или аналогичной ей для тел другой формы вычисляют значение безразмерной температуры Q в данной точке в заданный момент времени. Из Q определяют искомую температуру t = f(t, x). Анализ решения (1) позволяет выявить влияние величины числа Bi на нестационарную теплопроводность. Рассмотрим два предельных случая: Bi ® ¥ и Bi ® 0. Первый предельный случай:Bi ® ¥ (практически Bi >100). Для тела конечных размеров (l – конкретная конечная величина) этот случай соответствует условию a/l ® ¥, т. е. большим значениям коэффициента теплоотдачи a и сравнительно малым значениям коэффициента теплопроводности l.В этом случае сразу после начала процесса температура поверхности тела принимает и в дальнейшем сохраняет постоянное значение tc = tж = const. Следовательно, интенсивность процесса охлаждения (нагрева) определяется внутренним процессом теплопроводности в теле и зависит только от физических свойств и размеров тела. При этом общее решение (1) упрощается: из числа определяющих критериев выпадает критерий Bi. Так, для точек, расположенных в средней плоскости пластины (при Х = 0), уравнение для безразмерной температуры при Fo > 0,3 приобретает вид Второй предельный случай |
