Ответы на задачи 24 (С1)
 Скачать 1.99 Mb. Скачать 1.99 Mb.
|
|
and (x<=0) and (y>=0)
and (x>=0) and (y<=0) Два условия, выделенные синим цветом, можно записать в виде (x*y<=0). Поэтому условие для областей 2 и 3 переписываем в виде (y <= 1-x) and (y >= 2-2*x*x) and (y >= x*x-5) and (x*y <= 0) Получаем: if (y >= 0) and (y <= 2-2*x*x) or (y <= 1-x) and (y >= 2-2*x*x) and (y >= x*x-5) and (x*y <= 0) then write('принадлежит') else write('не принадлежит');
Н 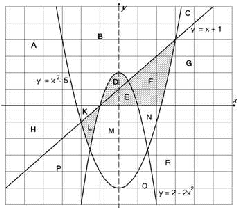 апомним программу: апомним программу:if y >= x+1 then begin if y <= 2-2*x*x then write('принадлежит') end else if y >= x*x-5 then write('принадлежит') else write('не принадлежит') В строке 1 ничего не выводится, значит ответ неверный. Такой вариант (отсутствие вывода) говорит о том, что первое условие выполнено, а второе – нет. То есть, эта область расположена выше прямой и выше параболы y = 2 - 2x2; это могут быть область A, B, C, H, K:
Теперь рассмотрим строку 2. Программа выдает ответ «принадлежит», что может быть
При этом ответ «принадлежит» неверный. Поскольку ВСЕ точки, для которых выполняются первые два условия, принадлежат заштрихованной области D, первый вариант исключается. Поэтому для второй строки первое условие ложно (точки ниже прямой), второе не проверяется, а третье – истинно (точки выше параболы y = x2 - 5); эти области не заштрихованы, поэтому это могут быть только области M и N:
Третья строка. Сообщение «не принадлежит» выводится для точек, которые ниже прямой и ниже параболы y = x2 - 5, эти точки не принадлежат выделенной области; это могут быть области G, P, Q, R.
Наконец, для четвертой строки третье условие не проверяется, значит, первое истинно. Второе проверяется, и результат верный. Это значит, что второе условие истинно и выведено сообщение «принадлежит». Это точки, расположенные выше прямой и ниже параболы y = 2 - 2x2, то есть область D.
Для того, чтобы написать правильную программу, составим одно сложное условие. Проще всего сложить полную область из трех:
and (x <= 0) Остается объединить эти области с помощью операции ИЛИ: if (y >= x+1) and (y <= 2-2*x*x) or (y <= x+1) and (y >= 0) and (y >= x*x-5) or (y <= x+1) and (y >= 2-2*x*x) and (y >= x*x-5) and (x <= 0) then write('принадлежит') else write('не принадлежит'); Более хитрый способ:
(y <= x+1) and (y >= 2-2*x*x) and (y >= x*x-5) and (x>=0) and (y>=0)
and (x<=0) and (y<=0) Два условия, выделенные синим цветом, можно записать в виде (x*y>=0). Поэтому условие для областей 2 и 3 переписываем в виде (y <= x+1) and (y >= 2-2*x*x) and (y >= x*x-5) and (x*y >= 0) Получаем: if (y >= 0) and (y <= 2-2*x*x) or (y <= x+1) and (y >= 2-2*x*x) and (y >= x*x-5) and (x*y <= 0) then write('принадлежит') else write('не принадлежит');
if a + b < n then writeln(0) else if a < b then if a < n then writeln(a+1) else if b < n then writeln(b+1) else writeln(n+1); Выделив структуру заданой программы получаем 4 вложенных условия. Для заданных исходных данных первое условие a + b < n = 3 + 6 < 5 ложно, второе a < b = 3 < 6 истинно, третье a < n = 3 < 5 истинно, поэтому программа выведет значение a + 1 = 3 + 1 = 4. Для того, чтобы ответить на второй вопрос, заметим, что программа ничего не выводит, если первое условие ложно, и второе тоже ложно. Например, это может быть при n = 5, a = 6, b = 3. Теперь нужно разобраться, какое решение является правильным. Представим модель задачи в виде трёх лент длиной a, b и n. Ленты длиной a, b соеднены вместе, а лента длиной n двигается относительно границы между первыми двумя, но так, чтобы не выйти за границы соединённой полосы «a+b». Варианты, которые нам нужно подсчитать, отличаются только положением границы, обозначенной красной линией.   Очевидно, что при a+b Если a ≥ n, то все вынутые шары могут быть красными (1 вариант), кроме того, ленту длиной n можно сдвинуть вправо на min(b,n) вправо, поэтому для этого случая |
