Ответы на задачи 24 (С1)
 Скачать 1.99 Mb. Скачать 1.99 Mb.
|
|
k:= 0; s:= 1; Это значит, что значение k=1 мы уже включили в сумму, но значение переменной k ещё не обновили. Проследим, как будет фактически изменяться значение переменной s из-за этой ошибки: s = 1 1+1=2 2+1/2=2,5 2,5+1/3=2,833 k=0 k=1 k=2 k=3 А вот как нужно было (результат k=0 означает, что ни одного натурального k, удовлетворяющего условию задачи, не существует): s = 1 1+1/2=1,5 1,5+1/3=1,833 1,833+1/4=2,083 k=0 k=1 k=2 k=3 Представим эти данные на диаграмме: 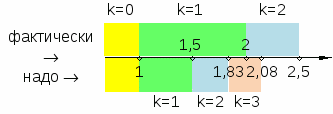 k=0 Из этой схемы видно, что при конечном значении s не более 1,5 программа выдаёт правильный ответ!
Было: k:=0; Исправление: k:=1;
Было: write(k); Исправление: write(k-1);
В программе сделано несколько ошибок, и в некоторых случаях они могут скомпенсировать друг друга. Во-первых, цикл заканчивается, когда sa, кроме того, после суммирования в цикле значение k ещё увеличивается! Поэтому мы всегда находим k, которое на 2 больше правильного значения. С другой стороны, перед циклом стоит два присваивания: k:= 1; s:= 1; В теле цикла это же значение k на первом шаге будет добавлено к сумме, то есть, единицу мы добавляем два раза! Проследим, как будет фактически изменяться значение переменной s из-за этой ошибки: s = 1 1+1=2 2+1/2=2,5 2,5+1/3=2,833 k=1 k=2 k=3 k=4 А вот как нужно было: s = 1 1+1/2=1,5 1,5+1/3=1,833 1,833+1/4=2,083 k=0 k=1 k=2 k=3 Представим эти данные на диаграмме: 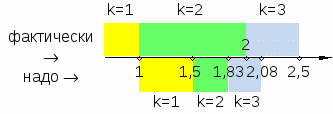 Из этой схемы видно, что при конечном значении s в интервалах 1,5 < s < 1,83 и 2 < s < 2,083 программа выдаёт правильный ответ!
Было: s:=1; Исправление: s:=0;
Было: write(k); Исправление: write(k-2);
while N > 0 do begin digit := N mod 10; ... N := N div 10; end; Вместо многоточия в программе стоит оператор if digit < 7 then sum := sum + 1; Это значит, что если очередная цифра оказалась меньше 7, сумма увеличивается на единицу (!). Так как в начале сумма равна 0, после окончания цифра в переменной sum будет количество цифр, меньших 7 (а не их сумма, как нам нужно по условию!). Обратим внимание на оператор вывода: writeln(digit); Он выводит последнее значение цифры, которое оказалось в переменной digit (а не сумму цифр, меньших 7, как требуется по условию!). Поскольку цифры перебираются с конца числа, это будет самая первая цифра этого числа. Таким образом, уже готовы все ответы:
Было: sum:=sum+1; Исправление: sum:=sum+digit;
Было: writeln(digit); Исправление: writeln(sum);
read(n) 1 k := 1 1 n > 0 да n := n – k 0 k := k + 1 2 n > 0 нет writeln(k) 2 Посмотрим, какой ответ должен был быть получен. Для N = 1 выполняется строгое неравенство 1 + 2 > N, а при предыдущем значении k = 1 неравенство 1 > N не выполняется. Поэтому программа выдаёт верный ответ, это и есть ответ на второй вопрос. Аналогично трассировкой находим, что при N = 2 программа выдает неверный ответ k = 3: read(n) 2 k := 1 1 n > 0 да n := n – k 1 k := k + 1 2 n > 0 да n := n – k -1 k := k + 1 3 n > 0 нет writeln(k) 3 А правильный ответ – 2, потому что сумма 1 + 2 уже больше, чем N = 2. Это ответ на первый вопрос. Попробуем понять, в чем причина – почему ответ неверный. Пусть для некоторого (минимального, искомого) K выполняется строгое неравенство 1 + 2 + … + K > N Мы фактически вычитаем из обеих частей этого неравенства сначала значение k = 1, потом k = 2 и т.д., причём остановиться в этом вычитании нужно тогда, когда выполнится условие 0 > N – (1 + 2 + … + K) В программе правая часть последнего неравенства хранится в переменной n, условие продолжения работы цикла – n > 0, поэтому цикл остановится при n <= 0, а не при n < 0, как требуется. Поэтому условие цикла нужно поменять на n >= 0. Одна ошибка найдена. Вторая ошибка в том, что сразу после вычитания значения k из n мы увеличиваем k на 1, то есть, выводим не последнее значение k, которое вычли, а следующее. Поэтому при выводе нужно уменьшить значение-результат на 1. Теперь попробуем установить закономерность в общем случае – когда исходная программа работает верно, а когда – неверно. Пусть K – это верное решение. По условию задачи оно определяется двумя неравенствами: 1 + 2 + … + (K–1) N < 1 + 2 + … + (K–1) + K В то же время программа выводит (с учётом последующего увеличения на 1) значение K, соответствующее условию 1 + 2 + … + (K–2) < N 1 + 2 + … + (K–2) + (K–1) Сравнивая части двух неравенств, выделенные зелёным фоном, находим, что такое возможно только при N = 1 + 2 + … + (K–1). При всех остальных значениях N программа работает неверно.
Было: while n > 0 do begin Исправление: while n >= 0 do begin;
Было: writeln(k); Исправление: writeln(k-1); Вариант 2 (А.Н. Носкин, г. Москва) Попробуем проанализировать, как работает существующая программа: k := 1; while n > 0 do begin n := n - k; k := k + 1; end; Заметим, что
Отсюда следует, что переменная n последовательно принимает значения N – 1, N – 1 – 2, N – 1 – 2 – 3 и т.д. где N – введённое число (равное начальному значения переменной n). С другой стороны, неравенство 1 + 2 + … + K > N можно записать в виде 2 + … + K > N – 1 3 + … + K > N – 1 – 2 … K > N – 1 – 2 – … – (K – 1) = n Выражение, выделенное маркером – это значение переменной n в тот момент, когда цикл должен остановиться. Поэтому условие останова цикла выглядит так: k > n. Следовательно, условие работы цикла – k <= n. Таким образом,
Было: while n > 0 do begin Исправление: while k <= n do begin;
read(n) 1 k := 1 1 n >=0 да k := k + 1 2 n := n – k -1 n >= 0 нет writeln(k) 2 Посмотрим, какой ответ должен был быть получен. Для N = 1 выполняется нестрогое неравенство 1 ≥ N, поэтому верный ответ – это 1. Программа выдаёт неверный ответ. Ото и есть ответ на первый вопрос. Попробуем понять, в чем причина – почему ответ неверный. Ученик хотел последовательно вычитать из правой части неравенства 1 + 2 + … + K ≥ N сначала значение k = 1, потом k = 2 и т.д., но фактически он вычитает k = 2, потом k = 3 и т.д., пропустив начальное значение 1, потому что перед вычитанием k увеличивается на 1. Тогда для исправления этой ошибки нужно изменить начальное значение k на 0. Одна ошибка найдена и исправлена. После этого исправления остановиться в вычитании нужно тогда, когда выполнится условие 0 ≥ N – (1 + 2 + … + K) В программе правая часть последнего неравенства хранится в переменной n, условие продолжения работы цикла – n >= 0, поэтому цикл остановится при n < 0, а не при n <= 0, как требуется. Поэтому условие цикла нужно поменять на n > 0. Вторая ошибка найдена. Сложнее всего ответить на второй вопрос: когда исходная программа выдаёт правильный ответ. Перебирая первые натуральные значения N, можно определить значение N = 4, при котором программа выдаст правильный ответ 3. Теперь попробуем установить закономерность в общем случае – когда исходная программа работает верно, а когда – неверно. Пусть K – это верное решение. По условию задачи оно определяется двумя неравенствами: SK–1 < N SK, где SK = 1 + 2 + … + K. При увеличении N переход к следующему значению K происходит при N = SK+1. В то же время программа выводит значение K, соответствующее условию SK–1–1 N < SK–1 Здесь при увеличении N переход к следующему значению K происходит при N = SK–1. Поэтому при N = SK–1 и N = SKрезультат работы программы будет неверный.  Итог: программа работает неверно, если значение N можно представить в виде N = 1 + 2 + … + Kили N = 2 + … + K В остальных случаях программа работает верно.
Было: k:=1; Исправление: k:=0;
Было: while n >= 0 do begin Исправление: while n > 0 do begin
|
