олимпиада 4 класс. Ответы по математике 4 класс
 Скачать 42.33 Kb.
|
|
Конец формы Ответы по математике 4 класс 1. (7 баллов) Замените звёздочки цифрами так, чтобы равенство стало верным и все семь цифр были различными: ** + ** = 175. Возможные ответы. 92 + 83 = 175 82 + 93 = 175 93 + 82 = 175 83 + 92 = 175 Дополнительных объяснений не требуется. Критерии проверки. • Приведён любой из возможных ответов — 7 баллов. • Приведён ответ, в котором какие-то две цифры совпадают, — 2 балла. 2. (7 баллов) В Солнечном городе меняют пряник на 6 сушек, а за 9 сушек дают 4 баранки. Сколько баранок дают за 3 пряника? Решение. Если за один пряник дают 6 сушек, то за 3 пряника дадут 3 × 6 = 18 сушек. 18 сушек — это 2 раза по 9 сушек. Значит, за них дадут 2 раза по 4 баранки, т. е. 8 баранок. Критерии проверки. • Любое верное и обоснованное решение — 7 баллов. • Приведены верные начальные рассуждения, а далее сделаны неверные выводы или не сделано никаких выводов — 2 балла. • Решение полное, но допущена одна арифметическая ошибка — 2 балла. • Только верный ответ — 1 балл. 3. (7 баллов) Проведите два отрезка с концами на сторонах треугольника так, чтобы треугольник оказался разбит на два треугольника, один четырёхугольник и один пятиугольник. 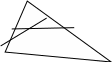 Критерии проверки. • Любой верный ответ — 7 баллов. • Треугольник разбит на нужные фигуры, но концы изображённых отрезков не на сторонах треугольника — 4 балла. 4. (7 баллов) Чтобы добраться от ствола к любому листу дерева, изображённого на рисунке, нужно на каждой развилке повернуть либо налево, либо направо. Например, для того чтобы добраться до листа с буквой А, нужно пройти так: ппплп (буква п — это поворот на развилке вправо, буква л — поворот влево). а) Напишите с помощью букв п и л путь к листу Б. 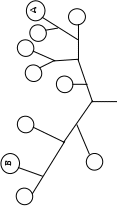 б) Дорисуйте на этом дереве ещё один лист так, чтобы на получившемся дереве был лист, соответствующий такому пути: пплплл. Напишите в листе, к которому ведет путь пплплл, букву В. Решение и ответ.  В а) лплп б) см. рисунок  Критерии проверки. • Даны верные ответы на оба пункта задания — 7 баллов.  • Дан верный ответ только на пункт б) — 5 баллов • Дан верный ответ только на пункт а) — 2 балла. 5. (7 баллов) У Вани, Тани и Оли есть 12 одинаковых по форме шариков: несколько жёлтых, несколько синих и несколько красных. Они разложили шарики по 4 штуки в три одинаковых пакета. Ваня сказал: «Смотрите, ни в одном пакете нет трёх одинаковых шариков!» Таня сказала: «Верно. Но и трёх разных шариков тоже нет ни в одном пакете!» Оля сказала: «И все пакеты получились разными!». Все трое были правы. Обязательно ли в каком-то пакете лежит два жёлтых и два красных шарика? Ответ. Да, обязательно. Решение. В каждом пакете есть шарики разных цветов, иначе Ваня был бы не прав. Но шариков трёх разных цветов не может быть ни в одном пакете, иначе была бы не права Таня. Значит, в каждом пакете есть шарики ровно двух цветов: 2 шарика одного цвета и 2 шарика другого цвета (так как трёх шариков одного цвета быть не может). Все пакеты получились разными, поэтому пара цветов в каждом пакете должна отличаться от пары цветов в другом пакете. Значит, в одном пакете было два жёлтых и два синих шарика, в другом — два синих и два красных шарика, а в третьем — два жёлтых и два красных шарика. Критерии проверки. • Любое верное и обоснованное решение — 7 баллов. • Приведён верный ответ, но обоснования не полны — 5 баллов. • Сказано без обоснований, что в каждом пакете по два шарика разных цветов, и отсюда получен правильный ответ — 2 балла. • Приведён только ответ — 0 баллов. |