Реферат по физике. Парадокс Гиббса

• Название: Парадокс Гиббса
• Дата: 19.10.2021
• Размер: 390.04 Kb.
• Имя файла: Реферат по физике.docx
• Тип: Реферат; #251354

МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ им. Н. Э. БАУМАНА

Реферат

На тему «Парадокс Гиббса»

Выполнила студентка: Шмонина Оксана Игоревна

Группа: РЛ6-21Б

Научный руководитель:

Виктор Петрович Левин

Зачтено /незачтено/

_____________________

Москва – 2021г.

Содержание:

1. Введение……………………..…………………………………………………………..………....3

1.1 Формулировка теории………………………...……………………………………………..…...3

1.2 Суть парадокса Гиббса………………………………………………………………………..…4

2. Эксперимент…………………………………………………………………………...………..….6

2.1 Вывод из эксперимента.………………………………………………………….…………........7

3. Объяснение автора…………………………………………………………………………..…….8

3.1 Решения парадокса Гиббса от других ученых……………………...………...……………..….9

3.2 Анализ различных трактовок парадокса ………………………………………………………11

3.3. Собственное объяснение парадокса Гиббса…………………………………………………..11

4. Заключение………………………………………………………………………………..………12

5. Список литературы………………………………………………………………………………1

1. Введение

1.1 Формулировка теории

Парадокс Гиббса — отсутствие непрерывности для энтропии(количественная мера беспорядка) при переходе от смешения различных газов к смешению тождественных газов. Например, при переходе от бесконечно мало отличающихся идеальных газов к тождественным, расчётное значение энтропии смешения падает скачком до нуля, что представляется неожиданным и нелогичным.

Хотя парадокс Гиббса касается поведения термодинамической энтропии, его объяснение выходит за рамки собственно термодинамики. Парадокс был сформулирован Дж. У. Гиббсом в 1875 г. одновременно с вариантом его объяснения. Сам Гиббс ничего парадоксального в поведении энтропии смешения не усматривал; термин «парадокс Гиббса» впервые был, вероятно, использован О. Видебургом (1894).

Парадокс Гиббса был сформулирован в рамках классической термодинамики, и его объяснение сначала искали в рамках этой теории. Затем, поскольку парадокс воспринимали как вывод, противоречащий фактам, для его объяснения начали привлекать представления других теорий. Однако объяснение парадокса Гиббса в рамках какой-либо теории не может служить объяснением этого парадокса, если он получен в рамках другой теории[6].

Но так как математические соотношения, как и законы логики, имеют силу для любой теории, можно ожидать, что математические и логические аспекты парадокса Гиббса, получаемого в различных теориях, если не тождественны, то подобны. В связи с этим, основываясь на результатах рассмотрения парадокса Гиббса в рамках классической термодинамики, выскажем ряд замечаний о формулировках этого парадокса, получаемых различными авторами в рамках статистической термодинамики, квантовой механики, теории информации[6].

Пример одной из формулировок парадокса Гиббса в рамках статистической термодинамики:

«Как известно, в стандартном статистическом подходе аддитивное выражение для энтропии получается после деления стат.суммы на N! где N – число одинаковых частиц… Если все частицы одинаковы, то стат.сумму следует делить на N!, если есть два сорта частиц, то ее следует делить на N1!N2!. Трудность возникнет, когда при сближении свойств частиц N2! скачком меняется до нуля и (N1+N2)! не является пределом N1!N2! по плавно меняющемуся параметру, различающему частицы. Данная особенность порождает скачкообразное изменение энтропии…»[7]

Цель работы: исследовать, чем является парадокс Гиббса, разобрать решения мировых ученых и сравнить их объяснения

Задачи:

• 
  Узнать, что такое парадокс Гиббса, объяснить природу данного феномена
  
• 
  Проанализировать мысленный эксперимент, который демонстрирует этот парадокс
  
• 
  Рассмотреть объяснения разных ученых и выяснить, имеет ли парадокс Гиббса решение
  

1.2 Суть парадокса Гиббса

Энтропия S идеального газа с температурой  Т, занимающего объём V, равна [4]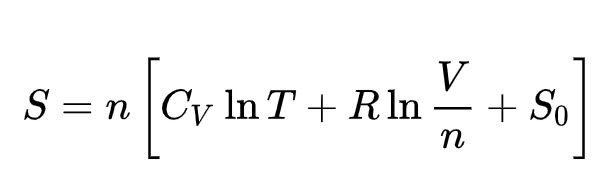



Рис.1. Формула Гиббса для энтропии идеального газа

{\displaystyle S=n\left[C_{V}\ln T+R\ln {\frac {V}{n}}+S_{0}\right],}

(

где n — число молей (количество вещества) идеального газа; С_V — мольная теплоёмкость газа при постоянном объёме; R — универсальная газовая постоянная (8.3144 Дж·К⁻¹·моль⁻¹); S₀ — не зависящая от n постоянная. Отметим, что в рассматриваемой формуле (Рис.1) использована традиционная для русскоязычной учебной литературы форма записи, из которой не видна «безразмерность» логарифмируемых величин.

В классической термодинамике изменение энтропии тела определяется как отношение количества теплоты, переданной телу в изотермическом процессе (при постоянной температуре), к температуре этого тела:

ΔS = ΔQ/T

Согласно первому закону термодинамики, количество теплоты, переданное телу, складывается из изменения внутренней энергии этого тела и совершенной над ним работы[4]:

ΔQ = ΔU + A

Если работа равна нулю, то количество теплоты, переданное телу, равно изменению его внутренней энергии:

ΔQ = ΔU

В этом случае изменение энтропии равно отношению изменения внутренней энергии тела к его температуре:

ΔS = ΔU/T

Согласно кинетической теории газов, внутренняя энергия идеального газа определяется как суммарная кинетическая энергия поступательного движения молекул газа внутри (замкнутого) сосуда [2]:

U = W_к

Последнюю можно выразить через среднюю квадратичную скорость движения молекул газа:

W_к = 1/2 N m v_ср²,

где N — общее число молекул газа в сосуде, m — масса одной молекулы, v_ср — средняя квадратичная скорость движения молекул.

Кроме того, суммарную кинетическую энергию молекул газа можно выразить через давление газа и объем сосуда:

W_к = 3/2pV,

где p — давление газа, а V — объем сосуда.

Из двух последних выражений видно, что если пропорционально (скажем, в два раза) увеличить количество молекул газа и объем сосуда, то давление газа не изменится, но суммарная кинетическая энергия молекул газа возрастет в такое количество раз:

(1/2)2Nmv_ср² = 3/2p2V = 2W_к

Отсюда автоматически следует, что в классической термодинамике энтропия аддитивна (то есть при изменении объема и количества молекул газа в некоторое количество раз энтропия этого газа изменяется в том же направлении и в такое же количество раз) [2]:

(1/2)2Nmv_ср² = 3/2p2V = 2W_к = 2U = T2S

С другой стороны, в статистической механике энтропия определяется как мера вероятности термодинамического состояния системы:

S = klnP,

где S — энтропия системы, k — постоянная Больцмана, а P — термодинамическая вероятность состояния, равная числу всех возможных распределений частиц по координатам и скоростям.

Для простоты ограничимся одними лишь координатами частиц. Пусть система из N частиц в объеме V находится в равновесном состоянии. Поскольку каждая из частиц может находиться в любой точке объема, то общее число состояний частиц равно объему в степени числа частиц:

P = V^N

Логарифм этого числа, умноженный на постоянную Больцмана, согласно определению, равен энтропии данной системы частиц:

S = klnV^N = kNlnV

Возьмем удвоенный объем с удвоенным числом частиц:

S₂ = k2Nln2V

Поскольку в классической термодинамике энтропия аддитивна, то энтропия вдвое большей системы должна быть в два раза больше энтропии исходной системы, но здесь это не получается:

S₂ — 2S = k2Nln2V — k2NlnV = k2N(ln2V — lnV) = k2Nln2

То есть, статистическая энтропия неаддитивна, в чем и заключается парадокс Гиббса.
2. Эксперимент

Проведем мысленный эксперимент: вместо одной перегородки в закрытом сосуде (Рис.2 ) поставим вплотную две перегородки, каждая из которых способна пропускать только один газ. Перегородка a пропускает только газ 1, перегородка b - только газ 2.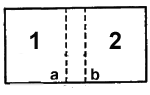


Рис.2 Закрытый сосуд, где 1 – газ 1, 2 – газ 2, a и b - перегородки
Убираем перегородку b. Газ 1 квазистатически расширяется на весь объем, совершая работу. Состояние газа 2 при этом не меняется.

Так как температура поддерживается постоянной, приращение энтропии газа 1 (Рис.3):



Рис.3 Формула приращения энтропии газа 1, где R — универсальная газовая постоянная, V – объём закрытого сосуда, V₁ – объем, который заполняет газ 1, v₁ – кол-во газа 1
Далее убираем перегородку. Происходит аналогичное квазистатическое расширение газа 2, а газ 1 своего состояния при этом не меняет. Приращение энтропии газа 2 (Рис.4) [3]:



Рис.4 Формула приращения энтропии газа 2, где R — универсальная газовая постоянная, V – объём закрытого сосуда, V₂ – объем, который заполняет газ 2, v₂ – кол-во газа 2

Общее приращение энтропии всей системы равно сумме приращений энтропии каждого газа. Приращение энтропии всей системы будет положительным, т.к. объем всей системы больше первоначального объема каждого газа. Энтропия возрастет.
2.1 Вывод из эксперимента
В результате мысленного эксперимента приращение энтропии системы будет такой же, как и при смешивании в реальной системе с одной перегородкой. Это доказывает, что самопроизвольный процесс смешения различных газов (пусть это различие будет даже сколь угодно малым) в адиабатической оболочке действительно необратим.
Но, если газы тождественны, то приращение энтропии в результате аналогичных рассуждений должно было бы сохраняться. Однако конечное состояние такой системы макроскопически ничем не будет отличаться от начального. Энтропия возросла, а состояние системы не изменилось. Если при смешении одинаковых газов ничего не происходит, может ли меняться энтропия системы? В этом и состоит парадокс Гиббса.

3. Объяснение автора

Пытаясь разрешить это противоречие, Гиббс обратил внимание на то, что статистическую энтропию можно сделать аддитивной, если считать неразличимыми состояния, образованные одинаковыми частицами. Перестановки таких частиц не изменяют макросостояния системы, поэтому все эти микросостояния можно считать одним состоянием. Число всех возможных перестановок N одинаковых частиц равно N!, то есть факториалу числа N. При очень большом количестве частиц (как в обычных термодинамических состояниях) N! с достаточной степенью точности можно заменить на N^N. Тогда приведенное выше выражение для статистической энтропии можно заменить следующим:

S = k*ln(V^N/N^N) = k*ln(V/N)^N = k*N*ln(V/N)

(Деля V^N на N^N мы исключаем из рассмотрения перестановки одинаковых частиц. Предполагается, что система состоит только из одинаковых частиц.)

Определенная таким образом энтропия оказывается аддитивной.

Однако такое решение парадокса Гиббса не следует ни из каких физических соображений и представляет собой простую «подгонку» решения под необходимый ответ. Неразличимость состояний одинаковых частиц имеет место в квантовой статистике, но там она физически вполне обоснована, поскольку в квантовой механике состояния частиц оказываются в каком-то смысле даже более реальными, чем сами частицы. Такие частицы нельзя «пометить» (например, различными пространственными координатами), поэтому их перестановки не изменяют макросостояния системы. В классической же статистике одинаковые частицы считаются «мечеными» (например, различаются теми же пространственными координатами), поэтому их перестановки изменяют макросостояние системы. Это означает, что либо классическая термодинамическая энтропия имеет квантовую природу, либо она не имеет никакого отношения к статистической энтропии.

Существует и еще одно возражение против такого решения парадокса Гиббса. Дело в том, что классическая термодинамическая энтропия не различает не только одинаковые частицы, образующие рабочее тело тепловой машины, но даже разные частицы. Для полноценной работы такой машины безразлично, из каких частиц состоит ее рабочее тело — разных или одинаковых, — важно лишь, чтобы они образовывали газ, не слишком сильно отличающийся по своим свойствам от идеального газа. В то же время статистическая энтропия четко различает разные и одинаковые частицы. Пусть, например, газ в объеме V состоит из двух сортов частиц. Тогда статистическая энтропия такого газа (с учетом ее аддитивности) равна[4]:

S = k*ln(V^N₁ ^{+ N}₂)/N₁!N₂!

Будем теперь изменять свойства частиц так, чтобы различия между ними постепенно исчезали, вплоть до полной одинаковости частиц. Пока различие сохраняется, сохраняется и прежнее выражение для энтропии. Но как только различие исчезает, то деление V^N₁^+N₂ на N₁!N₂! заменяется делением на (N₁ + N₂)! и энтропия скачком изменяется. То есть, даже с учетом поправки на аддитивность, статистическая энтропия не тождественна классической термодинамической энтропии.
3.1. Решения парадокса Гиббса от других ученых

Большинство физиков сегодня предпочитают первый вариант, хотя вполне осознают его недостатки. Поскольку первоначально понятие энтропии было введено на основе анализа работы классической тепловой машины, то никакие макроскопические параметры этой работы — энергия, энтропия, теплота, температура и т. д. — не требуют для своего обоснования привлечения квантовомеханических понятий. Необходимость в этом возникает пока только в случае энтропии и только в случае ее статистической интерпретации. Но если этот случай имеет под собой глубокую физическую природу, то квантовомеханические понятия должны быть нужны и для обоснования всех других макроскопических термодинамических параметров, а вот это как раз и не так. К примеру, кинетическая теория газов также опирается на статистическую механику, но довольствуется рамками классической статистики. [2]

Решения, отвергающие само существование парадокса (решение А. Зоммерфельда)

Логика рассуждения исследователей, отвергающих само существование парадокс Гиббса, следующая. Парадокс сводится к скачку в поведении энтропии смешения ΔS при непрерывном сближении некоторых параметров, характеризующих смешиваемые газы. Если такое непрерывное сближение противоречит законам физики, то есть если различия между газами могут изменяться только дискретно, парадокс Гиббса исчезает: нет ничего удивительного в том, что при дискретном изменении параметров газов свойства их смеси также изменяются дискретно.

Квантовые дискретные решения

Квантовое дискретное решение парадокса Гиббса от решений, отвергающих само существование парадокса, отличает признание существования парадокса, дискретность энтропии смешения воспринимают как естественный результат дискретности вещества, правильная зависимость энтропии газа от числа частиц (количества вещества) вытекает из квантовой статистики неразличимых частиц, а независимость энтропии смешения от свойств газов рассматривают как очевидное следствие допущения об их идеальности.

Квантовые решения на основе принципа непрерывности

И. фон Нейман, А. Ланде, М. Дж. Клайн, В. Л. Любошиц и М. П. Подгорецкий, рассматривая парадокс Гиббса, исходят из принципа непрерывности: непрерывное увеличение причин ведёт к непрерывному же увеличению эффекта; бесконечно малая причина никогда не произведёт конечного эффекта. Даваемое Любошицем и Подгорецким решение парадокса заключается, во-первых, в утверждении, что существуют ситуации, когда параметры близости могут изменяться непрерывно, и, во-вторых, в доказательстве того, что в этом случае величина энтропии смешения газов также меняется непрерывно и не испытывает никакого скачка при переходе от близких газов к одинаковым: парадокс Гиббса исчезает.

Операциональные решения (дискретное решение Бриджмена)

Согласно П. У. Бриджмену в экспериментальных процедурах, связанных с идентификацией двух данных порций газов, по мере их сближения по степени подобия друг другу наступает разрыв, разделяющий ситуацию, когда идентификация газов как разных реально возможна, от ситуации, когда такая идентификация уже реально невозможна. Этот разрыв и соответствует, по мнению Бриджмена, парадоксальному скачку энтропии. Принимая условность различимости или неразличимости газов, связанную с недостаточной разрешающей способностью используемого с этой целью экспериментального устройства, следует принять дискретность и условность параметра различия газов. Если имеются лишь грубые экспериментальные средства, так что параметр различия нельзя считать отличающимся от нуля, то следует принять отсутствие парадоксального скачка энтропии. Если же параметр различия измерим, то необходимо считаться с существованием скачка энтропии. Следовательно, существование или отсутствие скачка энтропии смешения, предсказываемое теорией, зависит от точности определения различия смешиваемых газов, доступной при имеющейся экспериментальной технике.

В принадлежащем Д. Тер Хаару и Г. Вергеланду непрерывном операциональном решении парадокса Гиббса фигурирует не только допущение о связи энтропии смешения с разрешающей способностью опознающего устройства, но и представление о том, что величина энтропии смешения существенным образом определяется ещё и принятыми в данное время физическими теориями, связывающих термодинамическую энтропию с информационной.

3.2 Анализ различных трактовок парадокса

Решить парадокс Гиббса означает установить причины скачка энтропии смешения ΔS при переходе от смеси сколь угодно близких газов к смеси одинаковых газов. В литературе описано множество самых разнообразных попыток решения парадокса Гиббса, однако появление всё новых и новых вариантов решений парадокса говорит об отсутствии общепринятого ответа на поставленный вопрос. [3]

Изучив различные решения парадокса Гиббса от некоторых физиков, мы можем поделить трактовки ученых на три категории. Первая предполагает само отсутствие парадокса или дискретность энтропии как естественный результат вещества (решение А. Зоммерфельда и квантовые дискретные решения), вторая категория подразумевает непрерывность увеличения энтропии без «скачка» (трактовка В. Л. Любошица и М. П. Подгорецкого), и третья категория считает, что парадокс Гиббса можно разрешить, учитывая не только свойства экспериментального вещества, но и свойства и способности экспериментальных установок (дискретное решение Бриджмена).

Такое разнообразие решений объясняется различиями в квантовой и классической статистике, классической-термодинамической и статистической энтропии, сложностью вычисления разрыва, разделяющего ситуацию, когда идентификация газов как разных реально возможна и наоборот, а также недостаточной точностью вычислений экспериментальных устройств.

3.3. Собственное объяснение парадокса Гиббса

Проанализировав решения многих ученых, у меня сформировалось свое объяснение парадокса Гиббса, основанное на трактовке П. У. Бриджмена. Его операциональные решения парадокса Гиббса исходят из представления о необходимости учёта при рассмотрении некоторых физических вопросов не только свойств исследуемых объектов, но и свойств экспериментальных установок, с помощью которых эти объекты исследуются. Я считаю, что разрешение парадокса Гиббса не является возможным, пока точность экспериментальных приборов не возрастет до необходимой (точность идентификации параметров газов как разных веществ). Простое анализирование без эксперимента не сможет объяснить данный феномен.

Чтобы найти разрешение парадоксу Гиббса, требуется провести тщательное наблюдение за состоянием обоих газов. С точки зрения аксиоматической термодинамики, к системе из двух газов нельзя применять мысленный эксперимент, приведенный в данном реферате, так как неясно, как провести соответствующий равновесный процесс. Этой проблемы можно избежать, если использовать две полупроницаемых перегородки, каждая из которых пропускает газ только одного сорта. Если изначально они соединены, то не будут пропускать ни один из газов. Постепенно раздвигая их, можно осуществить квазистатический процесс смешения. В том случае, если по обе стороны находится один и тот же газ, соответствующих перегородок в принципе не существует и парадокс исчезает. Однако можно представить себе последовательность таких экспериментов, в каждом из которых используются какие-то газы, всё меньше и меньше отличающиеся по свойствам. Тогда получится, что для одного и того же газа изменения энтропии не происходит, в то время как для любых двух газов, бесконечно близких по свойствам, существует вполне определённый конечный скачок энтропии в процессе. Подобное отсутствие непрерывности изменения энтропии само по себе парадоксально. Объяснить его можно только в рамках квантовой механики: существует конечное количество различных молекул, различающихся хоть в чём-нибудь по свойствам. [3]

Таким образом, непрерывно менять свойства газов нельзя, и конечный скачок энтропии связан с принципиальной разницей между различными газами. Да и в парадоксе Гиббса речь идет не о реальных конкретных объектах, имеющих бесчисленное множество свойств, связи которых друг с другом и с окружающей действительностью можно изучать десятилетиями, а об идеальных газах – абстрактных, идеализированных объектах. Это говорит о том, что провести нужный эксперимент либо не является возможным в принципе, либо не возможен в настоящее время в силу отсутствия необходимых экспериментальных устройств.

4. Заключение

Парадокс Гиббса является одним из самых загадочных физических парадоксов. Он возникает при рассмотрении довольно простых вопросов, касающихся энтропии смеси или энтропии смешения идеальных газов, однако более ста лет не имеет общепринятого объяснения. Определяемая так энтропия смеси и энтропия идеального газа являются функциями разного вида: формула первой функции содержит слагаемое, которого нет в формуле второй функции. Однако они ошибочно считаются функциями одного вида. Это влечет различные необъяснимые (парадоксальные) следствия — различные формулировки парадокса Гиббса. До сих пор нет ответа на вопрос: как устранить парадокс Гиббса? Этот вопрос должен стать предметом отдельного исследования. [5]

Для того чтобы экспериментально обнаружить предсказываемый теорией эффект, необходимо вначале сформулировать идею, которую предполагается положить в основу соответствующего опыта, а затем продумать варианты постановки эксперимента и оценить возможности их претворения в жизнь. На протяжении всего XX века раз за разом придумывали всё новые и новые способы опытным путём удостовериться в реальности существования парадокса Гиббса, и раз за разом же убеждались в невозможности их реализации. Гипотеза Ван дер Ваальса о принципиальной невозможности экспериментальной проверки существования парадокса Гиббса остаётся недоказанной, но на практике парадоксальный скачок энтропии смешения до сих пор не поддаётся измерению[6].

5. Список литературы

1. Хазин М. Л., Чернавский Д. С. Краткие сообщения по физике ФИАН, N 11, 28 (2000)

2. Губин В. Б. «Физические модели и реальность» (Проблема согласования термодинамики и механики) Алматы, 1993. -231 с.
3. Базаров И. П. Заблуждения и ошибки в термодинамике. — 2-е изд., испр. — М.: Едиториал УРСС, 2003. — 120 с. — ISBN 5-354-00391-1.

4. Гиббс Дж. В. Термодинамика. Статистическая механика / Отв. ред. Д. Н. Зубарев. — М.: Наука, 1982. — 584 с. — (Классики науки).

5. Игнатович В. Н. Парадокс Гиббса с точки зрения математика: Монография. — Киев: Издательская группа «АТОПОЛ», 2010. — 80 с.: Библиогр.: с.75-78. ISBN 978-966-2459-01-2

6. Хайтун С. Д. История парадокса Гиббса. — М.: Наука, 1986. — 168с.

7. Губин В. Б. Некоторые требования к правильному разрешению парадоксов Гиббса // Журнал физической химии. — 1985. — Т. 59, вып. 2. — С. 517-520.