параметрический критерий сравнения 2 независимых групп. Параметрический критерий Стьюдента сравнения двух независимых выборочных совокупностей. Работа с двумя выборками
 Скачать 102.59 Kb. Скачать 102.59 Kb.
|
|
Параметрический критерий Стьюдента сравнения двух независимых выборочных совокупностей. Работа с двумя выборками. 1. Проверка гипотезы о равенстве средних двух нормальных генеральных совокупностей (малые независимые выборки (независимые выборки - выборки, полученные для разных объектов, связанных определенным исследованием), двухвыборочный t-критерий Стьюдента). t-критерий Стьюдента направлен на оценку различий величин 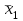 и и 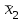 двух выборок Х1 и Х2, которые распределены по нормальному закону. Одним из главных достоинств критерия является широта его применения. Он может быть использован для сопоставления средних у зависимых и независимых выборок, причем выборки могут быть не равны по величине. В общем случае формула для расчета по t-критерию Стьюдента такова: двух выборок Х1 и Х2, которые распределены по нормальному закону. Одним из главных достоинств критерия является широта его применения. Он может быть использован для сопоставления средних у зависимых и независимых выборок, причем выборки могут быть не равны по величине. В общем случае формула для расчета по t-критерию Стьюдента такова: 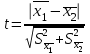 n≥30 n≥30Постановка задачи: получены 2 независимые выборки из нормальных генеральных совокупностей случайных величин Х1 и Х2, их объемы n1 и n2. По этим выборкам найдены 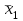 , , 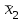 , , 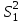 и и 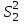 . .Требуется проверить гипотезу Н0: µ1= µ2. Прежде чем проверить данную гипотезу необходимо определить равенство дисперсий рассматриваемых совокупностей. Сделать это можно используя тест Фишера-Снедокерра. Для расчета критерия Стьюдента используются следующие формулы с учетом равенства дисперсий и объемов выборок. 1) Дисперсии равны 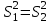 и объемы сравниваемых выборок различны, n1≠n2: и объемы сравниваемых выборок различны, n1≠n2: 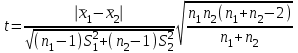 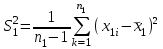 , , 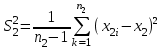 В этом случае число степеней свободы рассчитывается по формуле df= n1+n2-2. 2) Дисперсии равны 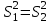 и объемы сравниваемых выборок равны, n1=n2: и объемы сравниваемых выборок равны, n1=n2: 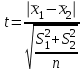 . .В этом случае число степеней свободы рассчитывается по формуле df=2n-2. 3) Дисперсии не равны 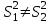 и объемы сравниваемых выборок различны, n1≠n2: и объемы сравниваемых выборок различны, n1≠n2: 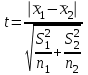 В этом случае число степеней свободы рассчитывается по формуле: 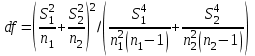 4) Дисперсии не равны 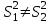 и объемы сравниваемых выборок равны n1=n2: и объемы сравниваемых выборок равны n1=n2: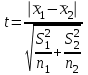 В этом случае число степеней свободы рассчитывается по формуле: 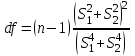 В приведенных формулах 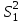 и и 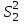 - дисперсии двух выборок, - дисперсии двух выборок, 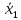 и и 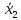 – средние выборочные, n1 и n2 – объемы выборок. – средние выборочные, n1 и n2 – объемы выборок.Методика проверки гипотезы о различии средних двух независимых групп, которые распределены по нормальному закону. Выдвигаем нулевую и альтернативную: Н0: µ1= µ2. Н1: µ1≠µ2. Вычисляем 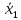 и и 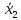 – средние выборочные, – средние выборочные, 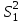 и и 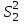 - дисперсии двух выборок. - дисперсии двух выборок.По критерию Фишера-Снедекора проверяем гипотезу о равенстве дисперсий групп. На основании результата вышеприведенного пункта выбираем соответствующую формулы расчета критерия Стьюдента и числа степеней свободы. Из таблицы распределения Стьюдента с учетом заданного уровня значимости (=0,05; 0,01)и числа степеней свободы находим критическое значение. Принимается решение о принятии или отклонении Н0. Если полученное значение tнабл. принадлежит критической области (tнабл>tкрит), то H0 отвергается: µ1 и µ2, а следовательно, 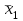 и и 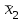 различаются значимо, т. е. их различие вызвано принципиальными причинами. Если tнабл. оказывается в области принятия нулевой гипотезы (tнабл различаются значимо, т. е. их различие вызвано принципиальными причинами. Если tнабл. оказывается в области принятия нулевой гипотезы (tнаблПример. Определить различие белка в составе плазмы крови здоровых и больных гепатитом. α=0,05.
Вычислим средние по двум выборкам: 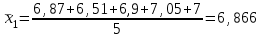 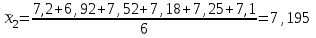 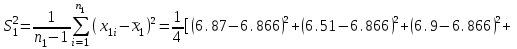 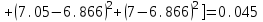 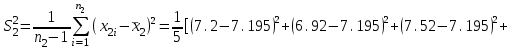 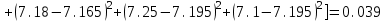 I) Для проверки гипотезы о равенстве дисперсий двух групп используем критерий Фишера-Снедекора. Выдвигаем нулевую и альтернативную гипотезы: Н0: D1=D2, H1: D1≠D2. α=0,05 Вычислим значение F – критерия Фишера 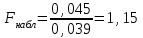 Числа степеней свободы df1=5-1=4 df2=6-1=5 По таблице Фишера найдем критическое значение: Fкрит (0,05; 4; 5)=5,19. Fнабл Вывод: D1=D2 Проведем проверку гипотезу о равенстве популяционных средних. II) Н0 – µ1=µ2 (различие белка в составе плазмы крови здоровых и больных гепатитом отсутствует). Н1 – µ1≠µ2 (есть различие белка в составе плазмы крови здоровых и больных гепатитом). α=0,05 Найдем t-критерий: 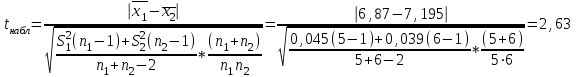 α=0,05 и для степени свободы df=n1+n2-2=5+6-2=9 определим критическое значение tкрит=2,26. tнабл > tкрит (2,63>2,26), то есть нулевая гипотеза отвергается. Заключение: при нормальном распределении и α=0,05 (доверительной вероятности р=0,95) существует статистическое различие белка в составе плазмы крови здоровых и больных гепатитом. Пример. Сравнительное исследование концентрации свинца в крови (в мг/100г) группы рабочих аккумуляторного завода Х1 (подвергавшихся профессиональному воздействию) и группы рабочих текстильной фабрики X2 (не подвергавшихся профессиональному воздействию), привело к следующим результатам: 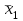 =0,08157 мг/100г, S1=0,0067 мг/100г, =0,08157 мг/100г, S1=0,0067 мг/100г, 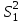 =4,489·10-5, n=7 =4,489·10-5, n=7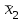 =0,03943 мг/100г, S2=0,00355 мг/100г, =0,03943 мг/100г, S2=0,00355 мг/100г, 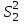 =1,26·10-5, n=7. =1,26·10-5, n=7.Число степеней свободы df=2*(7-1)=12. Предполагается, что 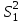 = =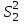 и исследуемый показатель в генеральной совокупности распределен по нормальному закону. и исследуемый показатель в генеральной совокупности распределен по нормальному закону.При α=0,05 проверяется Н0: µ1=µ2 против альтернативы Н1: µ1≠µ2. В соответствии с вышеприведенными числовыми данными tнабл.=19,6, tдвухст. кр.=2,18. Так как tнабл.>tдвухст. кр., нулевая гипотеза отвергается с заданным уровнем значимости. То же подтверждает расчет P, P<0,05. Вывод: условия работы значимо влияют на содержание свинца в крови рабочих. Для проверки нулевой гипотезы может служить интервальная оценка статистических параметров: доверительный интервал для генеральной средней или доверительный интервал для генеральной разности. 1. При сравнении выборочных средних рассчитываются доверительные интервалы для генеральной средней µ1и µ2: 95% доверительный интервал для средних: •Общая формула (большой размер выборки) 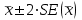 ; ;•Общая формула («небольшие» выборки) 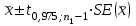 . .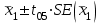 - доверительный интервал для генеральной средней µ1; - доверительный интервал для генеральной средней µ1;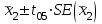 - доверительный интервал для генеральной средней µ2. - доверительный интервал для генеральной средней µ2.Где t05берется для 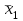 и и 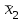 отдельно для каждого среднего значения. отдельно для каждого среднего значения.Если доверительные интервалы перекрывают друг друга, то разницу между 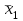 и и 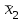 нельзя переносить на µ1 и µ2, поэтому нулевая гипотеза не отвергается, т.е. различия между вариантами признаются несущественными. Если доверительные интервалы не перекрывают друг друга, то различия между вариантами достоверны. нельзя переносить на µ1 и µ2, поэтому нулевая гипотеза не отвергается, т.е. различия между вариантами признаются несущественными. Если доверительные интервалы не перекрывают друг друга, то различия между вариантами достоверны.2. Нулевая гипотезу можно проверить также путем расчета доверительного интервала для генеральной разности D = µ1- µ2. для этого рассчитывают разность между выборочными средними d и ошибку разности средних. Важно знать, что: - Выборочное распределение разницы двух выборочных средних, оба которых получены из больших выборок, приближено к нормальному. - Центр этого выборочное распределение равен истинной разнице средних, 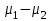 . .95% доверительный интервал для разницы средних: •Общая формула (большой размер выборки) 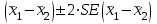 ; ;•Общая формула («небольшие» выборки) 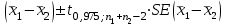 . .Стандартная ошибка разницы средних двух независимых выборок вычисляется иначе, чем для парных выборок: - В парном дизайне мы сокращали количество данных от двух выборок до одного набора данных, который включал в себя разницу между спаренными наблюдениями. - Формула для стандартной ошибки разницы (зависит от размера выборки двух групп и стандартного отклонения двух групп): 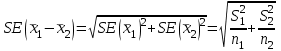 . .3. Если доверительный интервал для разности средних перекрывает нулевое значение и захватывает область отрицательных величин, то нулевая гипотеза не отвергается (различия между вариантами признаются несущественными). Если доверительный интервал лежит в области положительных величин, то Н0отвергается, т.е. разность между выборочными средними признается достоверной. Пример. Сравнение двух независимых групп: Исследование типов диеты «Низкоуглеводная диета по сравнению с низкожировой диетой среди страдающих тяжелой формой ожирения». - 132 человека с тяжелой формой ожирения были случайно распределены в одну из двух групп диет. - Участники наблюдались в течение 6 месяцев. Научный вопрос: Связано ли изменение веса с типом диеты?
Выражаясь статистически, существует ли ненулевая разница изменения веса среди участников на низкожировой диете по сравнению с участниками на низкоуглеводной диете? - 95% доверительные интервалы изменения веса в двух группах диет не пересекаются, но как количественно измерить эту разницу? - Интересующие нас показатели не «спарены»: Разные участники в каждой группе. - Для каждого участника было вычислено значение изменения веса (после диеты-до диеты): Но авторы сравнивают изменения веса в двух независимых группах! Как вычислить доверительный интервал разницы показателей? Поскольку обе выборки относительно большие (обе больше 60), мы знаем, что выборочное распределение выборочного среднего в двух группах близко к нормальному. Исходя из этого, разница показателей, которые распределены (приблизительно) нормально, имеет также нормальное распределение. 95% доверительный интервал для разницы средних: Лучшая оценка разницы популяционных средних на основе двух выборок: 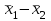 . Здесь . Здесь 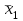 является средним значением изменения веса 64 участников на низкоуглеводной диете, а является средним значением изменения веса 64 участников на низкоуглеводной диете, а 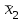 - среднее значение изменения веса 68 участников на низкожировой диете. - среднее значение изменения веса 68 участников на низкожировой диете.Итак, 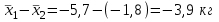 , поэтому формула для , поэтому формула для 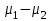 : : 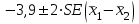 , где , где 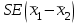 - стандартная ошибка разницы двух выборочных средних. - стандартная ошибка разницы двух выборочных средних.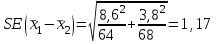 Таким образом, в этом примере 95% доверительный интервал для истинного значения разницы популяционных средних 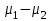 : : 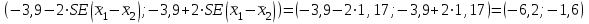 По завершению исследования: - «Участники на низкоуглеводной диете потеряли больше веса по сравнению с тем, кто был на низкожировой диете (95% доверительный интервал разницы потери веса между группами: от -1.6 до -6.2 кг; p<0.01». - Таким образом, придерживающиеся низкоуглеводной диеты потеряли на 3.9 кг больше; после учета случайной вариабельности выборки эта дополнительное уменьшение веса по сравнению с низкожировой диетой может быть от 1.6 кг до 6.2 кг. - Этот доверительный интервал не включает 0, предполагая наличие ассоциации на популяционном уровне между типом диеты (низкоуглеводная или низкожировая) и снижением веса. Задания. t-критерий Стьюдента для независимых выборок Препарат из группы антагонистов кальция, нифедипин, обладает способностью расширять сосуды, и его применяют при лечении ишемической болезни сердца. Измеряли диаметр коронарных артерий после приема нифедипина и плацебо и получили следующие две выборки данных диаметра коронарной артерии (в мм).
Позволяют ли приведенные данные полагать, что нифедипин влияет на диаметр коронарных артерий? 2. t-критерий Стьюдента для независимых выборок Стремясь отделить действие тетрагидроканнабинолов от действия дыма, исследователи изучили их действие при внутривенном введении. После ингаляционного введения бактерий крысам вводили спиртовой раствор тетрагидроканнабинолов, контрольной группе вводили этиловый спирт. В обеих группах было по n1=n2=36 животных. После введения тетрагидроканнабинолов доля погибших бактерий составила в среднем x1crednyaya=51,4%, в контрольной группе – x2=59,4%. Стандартные ошибки среднего составили соответственно SE1=3,2% и SE2=3,9%. Позволяют ли эти данные утверждать, что тетрагидроканнабинолы ослабляют антибактериальную защиту? ЛИТЕРАТУРА 1. А. Афифи, С. Эйзен. Статистический анализ. Подход с использованием ЭВМ/ М.: Мир, 1982. 488 с. 2. Боровиков, В. Statistica. Искусство анализа данных на компьютере: для профессионалов/ СПб.: Питер, 2001. 656 с. 3. Вентцель, Е. С. Теория вероятностей/ М.: Наука, 1969. 576 с. 4. Гмурман, В. Е. Руководство к решению задач по теории вероятностей и математической статистике/ М.: Высшая школа, 2001. 400 с. 5. Гмурман, В. Е. Теория вероятностей и математическая статистика/ М.: Высшая школа, 1972. 368 с. 6. Н. И. Инсарова, В. Г. Лещенко. Элементы теории вероятностей и математической статистики: учеб.-метод. пособие/ Минск: БГМУ, 2003. 66 с. 7. С. Н. Лапач, А. В. Чубенко, П. И. Бабич. Статистические методы в медико-биологических исследованиях с использованием Excel/ Киев: Морион, 2000. 319 с. 8. В. А. Медик, М. С. Токмачев. Руководство по статистике здоровья и здравоохранения/ М: Медицина, 2006. 528 с. 9. В. А. Медик, М. С. Токмачев, Б. Б. Фишман. Статистика в медицине и биологии: рук. в 2 т. Т. 1. Теоретическая статистика/ М.: Медицина, 2000. 455 с. 10. Ю. Н. Тюрин, А. А. Макаров. Статистический анализ данных на компьютере/ М.: Инфра-М, 1998. 528 с. 11. В. А. Фигурин, В. В. Оболонкин. Теория вероятностей и математическая статистика/ Минск: Новое знание, 2000. 206 с. 12. В. И. Юнкеров, С. Г. Григорьев. Математико-статистическая обработка данных медицинских исследований/ СПб.: ВМедА, 2002. 266 с. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

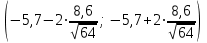 =
=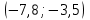
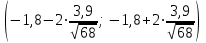 =
=