Передаточным отношением
 Скачать 238.03 Kb. Скачать 238.03 Kb.
|
 СОДЕРЖАНИЕ ВВЕДЕНИЕ 3 Цель настоящей курсовой работы -- проектирование механизмов по задаваемым параметрам (синтез механизмов) и комплексный анализ существующего шарнирно-рычажного механизма. 3 Для передачи движения между заданными в пространстве осями служат зубчатые механизмы (зубчатые передачи). Два цилиндрических зубчатых колеса образуют простейший передаточный механизм, состоящий из двух подвижных звеньев, входящих в две вращательные пары и одну высшую кинематическую пару. Основное требование, предъявляемое к этим механизмам, обеспечение постоянства передаточного отношения между звеньями. Эвольвентный профиль зуба обеспечивает это требование. 3 Передаточным отношением (U12) называют отношение угловой скорости (ω1) входного колеса к угловой скорости (ω2) выходного колеса. 3 ИСХОДНЫЕ ДАННЫЕ ДЛЯ ПРОЕКТИРОВАНИЯ. 4 ВВЕДЕНИЕЦель настоящей курсовой работы -- проектирование механизмов по задаваемым параметрам (синтез механизмов) и комплексный анализ существующего шарнирно-рычажного механизма.Для передачи движения между заданными в пространстве осями служат зубчатые механизмы (зубчатые передачи). Два цилиндрических зубчатых колеса образуют простейший передаточный механизм, состоящий из двух подвижных звеньев, входящих в две вращательные пары и одну высшую кинематическую пару. Основное требование, предъявляемое к этим механизмам, обеспечение постоянства передаточного отношения между звеньями. Эвольвентный профиль зуба обеспечивает это требование.Передаточным отношением (U12) называют отношение угловой скорости (ω1) входного колеса к угловой скорости (ω2) выходного колеса.Кулачковые механизмы так же относятся кмеханизмам с высшей кинематической парой, образованной входным звеном- кулачком и выходным звеном - толкателем. Теоретически кулачковыми механизмами можно осуществлять самые различные преобразования законов движения, задаваемых диаграммой перемещения толкателя (Si) в функции угла поворота кулачка (φi). На практике обычно используют те законы движения, которые обеспечивают кинематические и динамические требования к работе кулачкового механизма. Эти законы задаются для основных фаз движения толкателя: фазы удаления толкателя, когда толкатель поднимается из крайнего нижнего в крайнее верхнее положение и которой соответствует угол поворота кулачка (φу);фазы дальнего стояния толкателя, угол поворота кулачка (φд), и фазы возврата толкателя, когда толкатель опускается из крайнего верхнего положения в крайнее нижнее, угол поворота (φn).Для уменьшения износа кулачка толкатель снабжается роликом, контактирующим с кулачком. Что представляет собой комплексный анализ? Он включает в себя структурный, кинематический, силовой и прочностной анализ механизма. Структурный анализ механизма ставит своей целью обоснование класса механизма и установление формулы его строения, определяющих метод и последовательность кинематического и соловогоанализа механизма. Кинематический анализ механизма состоит в определении законов движения звеньев механизма по заданному закону движения его входного звена. Задачами кинематического анализа являются: определение положений звеньев, определение скоростей и ускорений. Силовой анализ механизма сводится к определению усилий, действующих на звеньях механизма при известных законах их движения. Задачами солового анализа являются: определение усилий на звеньях механизма, реакций в кинематических парах, уравновешивающей силы. Прочностной анализ механизма состоит в проверочном расчете прочности шатуна. Задачами этого расчета являются построение эпюр, определение «опасного сечения» и коэффициента запаса прочности для заданных формы и размеров сечения шатуна при действии на него полученных сил ИСХОДНЫЕ ДАННЫЕ ДЛЯ ПРОЕКТИРОВАНИЯ.Число зубьев колес Z₁= 14 , Z₂=17 Модуль зацепления m (мм) = 8 Угол удаления φy (град) = 100 Угол дальнего стояния φД (град)=130 Угол возврата φв(град)= 120 Ход толкателя h (мм) = 55 Частота вращения кривошипа n1 (мин-1) = 200 Длина кривошипа lAB (мм) = 40 Длина шатуна lBC (мм) = 190 Сила полезного сопротивления PC (H)=1260 Поперечное сечение шатуна – прямоугольник высотой h (мин) = 15 шириной b (мин) = 10 Массы звеньев: m₂ = 5.2 кг; m₃ = 2.4 кг. Положение кривошипа. ЛИСТ № 1 1. Геометрический синтез прямозубой эвольвентной зубчатой передачи внешнего зацепления. 1.1. Алгоритм расчета геометрии передачи. Основные размеры двух прямозубых эвольвентных зубчатых колес внешнего зацепления. 1.1.1. Угол зацепления передачи «в сборе» invαw 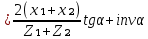 где inv (инволюта) – эвольвентная функция угла α, имеющая вид invα = tgα- α; для удобства вычислений существуют таблицы эвольвентной функции (инволют) для различных значений угла α.. 1.1.2. Диаметры делительных окружностей 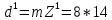 =112; =112; 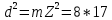 =136 =1361.1.3. Диаметры начальных окружностей dw₁ = d₁ 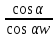 =118.03 =118.03dw₂ = d₂ 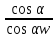 =143.33 =143.331.1.4. Межосевое расстояние 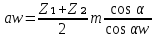 =130 =130Проверка 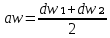 1.1.5. Диаметры основных окружностей 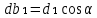 =105.25 =105.25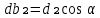 = 127.8 = 127.81.1.6. Диаметры окружностей впадин df1 = m (Z₁-2ha•-2c•+2x₁) = 97.44 df2 = m (Z₂-2ha•-2c•+2x₂)= 126.24 1.1.7. Диаметры окружностей вершин da1 =2aw – df2 – 2c•m=131.12 da2 = 2aw – df1 – 2c•m.=159.92 1.1.8. Высота зуба h1=h2= 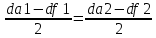 .=16.84 .=16.841.1.9. Шаг зацепления по дуге длительной окружности 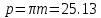 1.1.10. Толщина зуба по дуге делительной окружности S1 = 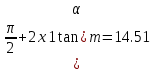 S2 = S2 = 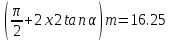 1.1.11. Шаг зацепления по хорде делительной окружности 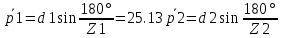 =25.13 =25.131.1.12. Толщина зуба по хорде делительной окружности 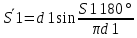 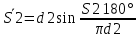 1.1.13. Толщина зуба по дуге окружности вершин Sa1 = da1 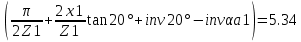 Sa2 = da2 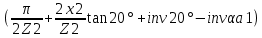 =4.38 =4.38Где cosαa1 = 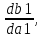 cosαa2 = cosαa2 = 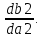 1.1.14. Коэффициент перекрытия ε = 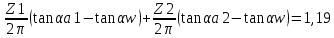 1.2. Построение картины зацепления. Последовательность построения следующая: 1.2.1. Выбираем масштаб построения М 1.2.2. В выбранном масштабе откладываем межосевое расстояние aw =130.68 . 1.2.3. Из центров О1 и О2 строим основные окружности диаметров db1 = 105.25 и db2 =127.8. 1.2.4. Проводим общую касательную к основным окружностям, А и В – точки касания. Точка пересечения (Р0) касательной АВ с линией О1О2 – полюс зацепления. 1.2.5. Строим начальные окружности колес диаметров dw1 =118.03 и dw2 =143.33 . Они обязательно должны касаться друг друга в полюсе зацепления Р0. Здесь же строим делительные окружности диаметров d1 =112 , d2 =136 и окружности вершин диаметров da1 = 131.12 и da2 =159.92. 1.2.6.По данным распечатки профиль зуба строится следующим образом: Для колеса 1 (Z1) По начальной окружности, начиная от точки Р0, откладываем толщину 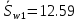 зуба по хорде этой окружности в сторону точки А. зуба по хорде этой окружности в сторону точки А.Эту хорду делим пополам и через полученную точку проводим ось симметрии зуба, соединяя эту точку с центром колеса. На основной, делительной и окружности вершин откладываем от полученной оси симметрии по данным распечатки половины толщины зуба, соответственно 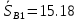 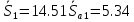 . Четыре полученные точки и симметричные им точки позволяют построит эвольвенту профиля зуба 1. . Четыре полученные точки и симметричные им точки позволяют построит эвольвенту профиля зуба 1.1.2.7. Ограничиваем профили зубьев окружностями вершин и впадин. При построении окружности впадин следует учитывать следующее обстоятельство: если rt Переходная часть (галтель ножки) зуба от эвольвенты или прямой окружности впадин изображается дугой 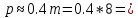 3.2 мм, которой сопрягаются эти элементы колеса. 3.2 мм, которой сопрягаются эти элементы колеса.Для колеса 2 (Z2) Повторяем построение п.1.2.6. По начальной окружности, начиная от точки Р0, откладываем толщину 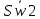 = 13.85 зуба по хорде этой окружности в сторону точки В. = 13.85 зуба по хорде этой окружности в сторону точки В.Эту хорду делим пополам и через полученную точку проводим ось симметрии зуба, соединяя эту точку с центром колеса. На основной, делительной и окружности вершин откладываем от полученной оси симметрии по данным распечатки половины толщины зуба, соответственно 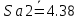 ., .,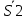 =16.25, =16.25,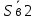 =17.16. Четыре полученные точки и симметричные им точки позволяют построит эвольвенту профиля зуба колеса 2. =17.16. Четыре полученные точки и симметричные им точки позволяют построит эвольвенту профиля зуба колеса 2.1.2.8 Для построение картины зацепления вычерчиваем три зуба каждого из колес, откладывая шаг зацепления (р) =25.13 по дуге (хорде) длительной окружности. 1.2.9 Прямая АВ, называемая линией зацепления, является геометрическим местом точек касания двух сопрягаемых профилей в процессе их зацепления. 1.2.10 Рабочий участок (ab) линии зацепления определяется точками пересечения окружностей вершин с прям АВ, этот участок лежит внутри прямой АВ. 2. Геометрический синтез профиля кулачка 2.1 Построение диаграммы перемещения толкателя в функции угла поворота кулачка. Построить профиль кулачка по диаграмме перемещения толкателя, еслиφy= 100 (град), φД = 130 (град), φв= 120 (град), h= 55 (мм), принимаем условно, что r0=h. 2.1.1 Откладываем на горизонтальной оси φ фазовые углы кулачка, приняв масштаб μφ=1 град/мм – один градус поворота равен одному мм на оси φ, т.е угол поворота φy= изображаемым отрезком 100 мм, и т.д.. 2.1.2 Делим отрезки, соответствующие углам удаления и возврата на восемь равных частей каждый. 2.1.3 В точках 8 и 9 восстанавливаем ординаты, равные ходу (h) толкателя, в нашем случае мм. 2.1.4 В точках 4 и 13 откладываем ординаты, равные половине хода толкателя. 2.1.5 Строим диаграмму перемещения толкателя в виде произвольной кривой, отвечающей следующим требованиям: На участках 0-4 и 13-17 кривая должна быть вогнутой; на участках 4-8 и 9-13 кривая должна быть выпуклой; точки 4 и 13 – точки перегиба; на участке 8-9 кривая параллельна оси φ. Полученная диаграмма показывает, что на участке, соответствующем углу удаления, толкатель поднимается вверх, достигая максимума (хода) в точке 8. На участке,соответствующем углу дальнего состояния (φД), толкатель неподвижен, он остается на расстоянии равном ходу толкателя до точки 9. На участке,соответствующем углу возвратаφв , толкатель возвращается в исходное положение. Эта диаграмма является основной для построения профиля кулачка, который должен обеспечить закон перемещения толкателя, представленного этой диаграммой. 2.2 Построение профиля кулачка. 2.2.1 Строим окружность радиусом r0=h с центром в точке О1. 2.2.2 В направлении, обратном вращению кулачка, откладываем фазовые углы φy= 100 (град), φД = 130 (град), φв= 120 (град). Углы откладываем, используя транспортир. 2.2.3 Делим углы удаления и возврата на восемь равных частей каждый и проводим через полученные точки радиальные прямые О1-1,О1-2,О1-3,… О1-17. 2.2.4 Начиная от окружности радиуса r0, на соответствующих радиальных прямых О1-1,О1-2,О1-3,… О1-17 откладываем отрезки 1-1,2-2,3-3,…16-16, измеренные на диаграмме перемещения толкателя. На участке, соответствующем фазовому углуφy, эти отрезки возрастают, на участке, соответствующем фазовому углуφД, они постоянны и на участкеφв они уменьшаются. 2.2.5. Соединяя концы этих отрезков плавной кривой, получаем профиль кулачка. 2.2.6 Для построения толкателя необходимо выбрать радиус ролика, которым толкатель касается кулачка. Радиус ролика r выбирается производительно, но должно выполняться условие r<0,4r0 .. 2.2.7 Строим окружность ролика касающуюся профиля кулачка в нулевой точке. Из центра ролика строим толкатель, который перемещается поступательно в направляющих. Расстояние от верхней части ролика до направляющих должно быть больше h. Лист № 2 3.Построение плана положений механизма. Принимаем стандартный масштаб построения µl=0, Определяем размеры звеньев для построения плана 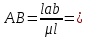 40 40BC= 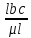 =190 =190откладываем заданное положение кривошипа, из точки В делаем засечку размером ВС на линии перемещения ползуна 3. Полученную точку С соединяем с точкой В. Центр масс (S1) звена АВ совпадает с точкой А, центр масс (S3) звена 3 совпадает с точкой С. 4.Структурный анализ механизма. 4.1. Обозначаем подвижные звенья механизма: Звено 1 – кривошип, совершает полный оборот вокруг точки А; Звено 2 – шатун, совершает плоскопараллельное движение; Звено 3 – ползун, совершает поступательные движения. 4.2. Определяем класс пар по Артоболевскому A(0,1) – 5 класса , В(1,2) – 5 класса, С(2,3) – 5 класса, С1(3,0) – 5 класса. 4.3. Определяем степень подвижности по Чебышеву: W = 3n- 2p5- p4 W = 3*3- 2*4 = 1 4.4. Выделяем элементы структуры механизма. Структурные группы 2-го класса по Ассуру представляют собой кинематическую цепь, состоящую из 2-х звеньев и 3-х кинематических пар. Формула строения механизма: Механизм 2 класса= механизм 1 класса (0,1) – группа 2 класса (2,3). Так как механизм является механизмом 2 класса, то его кинематический и силовой анализ проводится с помощью метода планов. 5.Кинематический анализ механизма. 5.1. План скоростей 5.1.1. Определяем угловую скорость звена 1. ω1 = 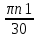 =20,93 =20,93Линейная скорость точки В равна Vn =ω1 * lAB= 0,83 Отрезок Pvb, изображающий скорость точки В на плане скоростей : Pvb =83 5.1.2 Масштаб плана скоростей µr= 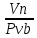 =0,01 =0,015.1.3. Векторное уравнение скоростей группы (2,3) VC= VB+VCB V = VCD+VCCD 5.1.4. Построение плана скоростей Из произвольной точки P,откладываем вектор Pvb перпендикулярно кривошипу АВ в направлении вращения кривошипа. Через точно b проводим прямую перпендикулярно СВ. Через Р проводим прямую параллельно направляющей, на пересечении получаем точку с. 5.1.5 Определяем скорости точек звеньев VC= Pvb * µ =0.83 VCB = cb * µ = 0.55 5.1.6. Величина угловой скорости равна ω2 = 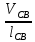 = 2.89 = 2.895.2. План ускорений. 5.2.1. Определяем ускорение точки В 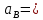 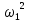 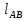 = 128,4=17.52 = 128,4=17.52Выбираем отрезок, изображающий на плане ускорений ускорение точки В, 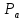 b= 142,6 мм. b= 142,6 мм.5.2.2. Масштаб плана ускорений 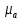 = =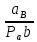 =0,25 =0,255.2.3. Векторное уравнение сложения ускорений группы (2,3) 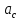 = =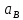 + +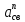 + + 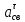 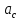 = =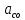 + + 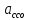 5.2.4. Построение плана ускорений. Из произвольной точки 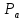 откладываем вектор откладываем вектор 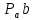 = 70мм параллельно звену АВ в заданном положении, направив его в сторону точки А звену АВ. = 70мм параллельно звену АВ в заданном положении, направив его в сторону точки А звену АВ.5.2.5. Определяем величину нормальной составляющей ускорения 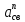 . .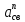 = = 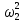 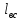 =1.58 =1.585.2.6. Определяем длину вектора bn , которым на плане ускорений изображается ускорение 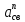 bn= 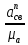 =6.32 =6.325.2.7. Из точки b вектора 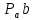 откладываем отрезок bn параллельно звену ВС, направив его в сторону точки В звена ВС. Из точки n восстанавливаем перпендикуляр к прямой bn. Из точки откладываем отрезок bn параллельно звену ВС, направив его в сторону точки В звена ВС. Из точки n восстанавливаем перпендикуляр к прямой bn. Из точки 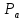 проводим прямую параллельно направляющей. Пересекаясь, прямые дают точку с. Соединяя точку с и точку b, находим точку проводим прямую параллельно направляющей. Пересекаясь, прямые дают точку с. Соединяя точку с и точку b, находим точку 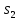 , лежащую посередине bc. , лежащую посередине bc.5.2.8. Определяем ускорение точек звеньев механизма и угловое ускорение звена ВС. 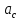 = =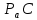 * * 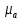 = 40 * 0,25=10 = 40 * 0,25=10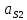 = =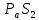 * * 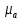 = 52 * 0.25=13 = 52 * 0.25=13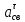 = =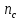 * * 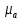 = 13 = 13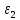 = =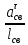 = 0.068 = 0.0686. Силовой анализ механизма. 6.1. Определяем внешние силы, действующие на звенья 2,3 структурной группы. Силы тяжести 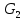 = = 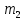 g =5.2*9,8= 50.96 g =5.2*9,8= 50.96 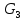 = = 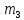 g =2,4*9,8=23.52 g =2,4*9,8=23.52Силы инерции 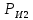 = = 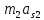 = 2,8*4=67.6 = 2,8*4=67.6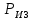 = = 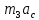 = 2.4*10=24 = 2.4*10=24Момент пар сил инерции 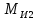 = =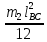 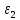 = 0,001 = 0,0016.2. В масштабе 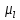 = 1 * = 1 *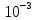 вычерчиваем структурную группу 2,3 в заданном положении и расставляем силы, действующие на звенья группы. вычерчиваем структурную группу 2,3 в заданном положении и расставляем силы, действующие на звенья группы. Сила полезного сопротивления 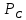 всегда направлена вдоль направляющей противоположно скорости точки С. Сила инерции всегда направлена вдоль направляющей противоположно скорости точки С. Сила инерции 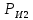 направлена параллельно вектору направлена параллельно вектору 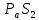 , но в противоположную сторону. Сила инерции , но в противоположную сторону. Сила инерции 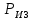 направлена параллельно вектору направлена параллельно вектору 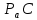 плана ускорений, но в противоположную сторону. Чтобы найти направление плана ускорений, но в противоположную сторону. Чтобы найти направление 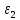 , вектор nc переносим параллельно самому себе, упирая стрелкой с в точку С звена ВС. Этот вектор вращает точку С относительно точки В по(против) часовой стрелки- это направление , вектор nc переносим параллельно самому себе, упирая стрелкой с в точку С звена ВС. Этот вектор вращает точку С относительно точки В по(против) часовой стрелки- это направление 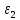 . Момент пар сил инерции . Момент пар сил инерции 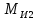 направлен противоположно угловому ускорению направлен противоположно угловому ускорению 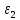 . Сила . Сила 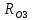 направлена перпендикулярно направляющей. В кинематической паре В приложены реакции отброшенных звеньев. Эти реакции неизвестны, поэтому представим их в виде составляющих, одна из которых направлена вдоль звена- нормальная составляющая направлена перпендикулярно направляющей. В кинематической паре В приложены реакции отброшенных звеньев. Эти реакции неизвестны, поэтому представим их в виде составляющих, одна из которых направлена вдоль звена- нормальная составляющая 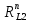 и вторая – перпендикулярно звену – тангенциальная составляющая и вторая – перпендикулярно звену – тангенциальная составляющая 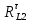 . .6.3. Запишем условие равновесия группы (2,3). 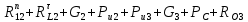 =0 =0Составим уравнение моментов относительно точки С для звена 2, уравнение равновесия имеет вид 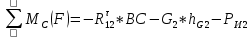 * *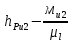 =0 =0Находим 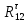 = - = - 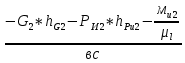 = -50.55 = -50.55Где ВС- длина звена 2, измеренная в мм на чертеже группы, 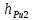 - плечо силы - плечо силы 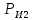 относительно точки С, это перпендикуляр, опущенный из точки С на линию действия силы относительно точки С, это перпендикуляр, опущенный из точки С на линию действия силы 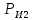 (измеряется в мм). (измеряется в мм).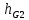 - плечо силы - плечо силы 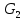 в мм. в мм.6.4. Решаем графически уравнение равновесия группы 2,3. Выбираем масштаб плана сил 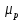 =0,25 =0,25Вычисляем длины векторов, которыми будут изображаться силы на плане сил в масштабе 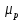 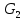 =12.74 мм , =12.74 мм , 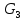 =5.88 мм, =5.88 мм, 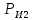 =16.9 мм, =16.9 мм, 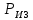 =6 мм, =6 мм, 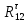 =12.63 мм, =12.63 мм, 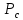 =315 мм. =315 мм.6.5. Построение плана сил Проводим линию действия силы 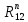 - прямую параллельную ВС. В - прямую параллельную ВС. Впроизвольной точке прямой откладываем вектор силы 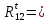 -26,69 мм -26,69 ммперпендикулярно этой прямой. Из конца вектора 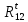 , откладываем вектор , откладываем вектор 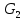 равный мм и т.д. в соответствии с векторным уравнением равновесия, т.е. складываем векторы геометрически. равный мм и т.д. в соответствии с векторным уравнением равновесия, т.е. складываем векторы геометрически.6.6. Определяем реакцию в средней кинематической паре С. Условие равновесия звена 2 имеет вид: 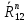 + +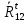 + +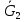 + +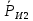 + +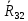 = 0 = 0Соединяя конец вектора 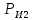 и начало вектора и начало вектора 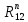 получаем реакцию в средней кинематической паре получаем реакцию в средней кинематической паре 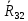 . .Полученные значения усилий и углов записываем в виде таблицы:
7. Построение расчетное схемы шатуна ВС. Изобразим шатун (звено 2) в заданном положении и покажем силы, действующие на шатун. Затем звено 2 с приложенными к нему силами поворачиваем в горизонтальное положение, оставляя углы такими же. Раскладываем силы, приложенные к звену 2 на вертикальные и горизонтальные составляющие. Горизонтальные составляющие: 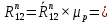 366*4=1464 366*4=1464 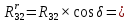 326.8 326.8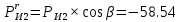 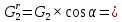 -25.48 -25.48Вертикальные составляющие 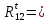 -50.55 -50.55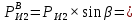 33.8 33.8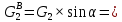 44.13 44.13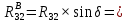 11.41 11.41Проверяем правильность исходных данных для расчетов на прочность . Так как шатун находится в равновесии, то должны выполняться условия: 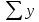 =0, =0, 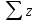 =0, =0, 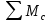 =0 =0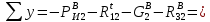 -33.8+50.55-44.13-11.41=0 -33.8+50.55-44.13-11.41=0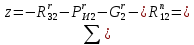 -326.8+58.54+25.48= 0 -326.8+58.54+25.48= 0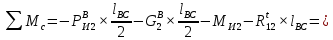 0 08.Определение геометрических характеристик сечения. Площадь поперечного сечения F = bh = 10*15 = 150 Момент сопротивления сечения 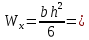 375 мм=0,375 м 375 мм=0,375 м 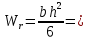 375 мм=0,375 м 375 мм=0,375 м9. Построение эпюры продольных сил. Разбиваем шатун ВС на два участка. Границами участков являются точки приложения сил (С, 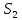 и В). Используем метод сечений. и В). Используем метод сечений.Участок 1. Выбираем произвольное сечение 1-1, отбрасываем правую часть и равновесие оставшейся левой части имеет вид 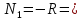 -326.8 -326.8Участок II. На участке I проводим в произвольном месте сечение II-II. Отбрасываем правую часть. Условие равновесия левой части 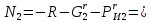 -326.8 +25.48 + 58.54 = 242.78 -326.8 +25.48 + 58.54 = 242.7810. Построение эпюры изгибающих моментов. Разбиваем шатун ВС на два участка. Границами участков являются точки приложения сил (С, 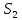 , и В). , и В).Для построения эпюры изгибающихся моментов используется метод сечений. Участок 1. Выбираем произвольное сечение 1-1 на расстоянии 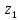 от точки от точки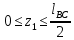 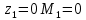 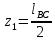 =47.5 =47.5 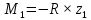 = -326.8*47.5=15.52 = -326.8*47.5=15.52Участок II Выбираем сечение II-II, отбрасываем правую часть. 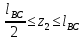 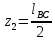 =47.5 =47.5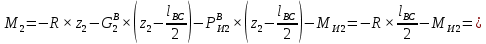 15.52 15.52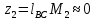 11. Расчет шатуна на прочность. Анализ эпюр продольных сил и изгибающих моментов показывает, что опасным является сечение, проходящее через центр масс 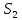 , шатуна, В этом сечении имеет , шатуна, В этом сечении имеетместо наибольшая продольная сила R= 326.8 максимальный изгибающий момент 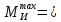 15.52 Шатун в сечении испытывает совместное действиеизгиба и сжатия. Для определения суммарных напряжений используем принцип независимости действия сил. 15.52 Шатун в сечении испытывает совместное действиеизгиба и сжатия. Для определения суммарных напряжений используем принцип независимости действия сил.10.1. Напряжение в опасном сечении от сжимающих сил. 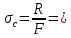 2.18 2.1810.2. Напряжение от изгиба в опасном сечении 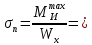 41,38 41,3810.3. Суммарное напряжение 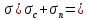 2.18+41,38=43.56 2.18+41,38=43.5610.4. Полагаем, что шатун изготовлен из Ст 3 , для которой допускаемое напряжение при изгибе 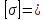 140 МП .Таким образом, в рассматриваемом случае 140 МП .Таким образом, в рассматриваемом случае условия прочности шатуна при сопротивлении на изгибе с растяжением 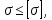 Коэффициент запаса прочности 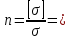 3.21 3.21Список использованной литературы 1. Аркуша А.И. Техническая механика. Теоретическая механика сопротивление материалов: Учебное пособие. М. В.Ш. 2002 2. Марченко С.И. Теория механизмов и машин: Ростов н/Д. Феникс, 2003 3. Попов С. А., Тимофеев Г.А. Курсовое проектирование по теории механизмов и механике машин: Учебное пособие. М. В.Ш. 2003 4. Сапрыкин В.Н. Техническая механика: Ростов н/Д. Феникс, 2003 5. Полушкин О.А., Ровеньков Е. Д., Кочетов В. А. Геометрический синтез механизмов с высшими кинематическими парами: Метод. указан. ДГТУ, 2005 |

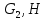
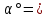 150
150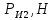
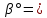 120
120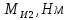
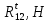
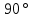
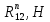
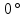
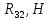
 2
2