Перегудов Ф. И., Тарасенко Ф. П
 Скачать 4.17 Mb. Скачать 4.17 Mb.
|
§ 7.5. ГРУППОВОЙ ВЫБОРВ человеческом обществе единоличное принятие решений является не единственной формой выбора. “Ум – хорошо, а два – лучше”, гласит поговорка, имеющая в виду тот случай, когда оба ума с одинаковыми намерениями пытаются найти хороший выбор. Этот случай мы и рассмотрим в данном параграфе (выбор в условиях конфликта будет рассмотрен в дальнейшем). ОПИСАНИЕ ГРУППОВОГО ВЫБОРА Итак, пусть на множестве альтернатив X задано n в общем случае различных индивидуальных предпочтений (для определенности будем говорить о бинарных отношениях) R1, R2, ..., Rn. Ставится задача о выработке некоторого нового отношения R, которое согласует индивидуальные выборы, выражает в каком-то смысле “общее мнение” и принимается за групповой выбор. Очевидно, что это отношение должно быть какой-то функцией индивидуальных выборов: R = F(R1, ..., Rn). Различным принципам согласования будут отвечать разные функции F. В принципе, т.е. теоретически, функции F могут быть совершенно произвольными, учитывать не только индивидуальные выборы, но и другие факторы, в том числе и исход некоторых случайных событий (например, бросания жребия), и главный вопрос состоит в том, чтобы правильно отобразить в функции F особенности конкретного варианта реального группового выбора. РАЗЛИЧНЫЕ ПРАВИЛА ГОЛОСОВАНИЯ Один из наиболее распространенных принципов согласования – правило большинства: принятой всеми считается альтернатива, получившая наибольшее число голосов. Правило большинства привлекательно своей простотой и демократичностью, но имеет особенности, требующие осторожного обращения с ним. Прежде всего оно лишь обобщает индивидуальные предпочтения, и его результат не является критерием истины. Только дальнейшая практика показывает, правильным или ошибочным было решение, принятое большинством голосов; само голосование – лишь форма согласования дальнейших действий*. Во-вторых, даже в простейшем случае выбора одной из двух альтернатив легко представить себе ситуацию, когда правило большинства не срабатывает: разделение голосов поровну при четном числе голосующих. Это порождает варианты: “председатель имеет два голоса”, “большинство простое (51 %)“, “подавляющее большинство (около 3/4)“, “абсолютное большинство (близкое к 100 %)“, наконец, “принцип единогласия (консенсус, право вето)“. —————————— * Этот вопрос, однако, формально находится вне нашего рассмотрения: ведь пока мы обсуждаем выбор в условиях определенности, а здесь речь зашла о выборе определенной альтернативы с неопределенными последствиями. Такие задачи мы рассмотрим позже. VOTING голосование GROUP CHOICE групповой выбор CONSENSUS консенсус MAJORITY RULE правило большинства CHOICE FUNCTION функция выбора Язык функций выбора (“глобальных функций множеств”) описывает результат выбора как некоторое подмножество множества альтернатив. Такое соответствие двух множеств без их поэлементного соответствия является новым понятием, расширяющим смысл термина “функция”. Оно позволяет описывать произвольные ситуации выбора, чего нельзя было сделать с помощью предыдущих двух языков. Коллективный выбор при любом правиле его осуществления сопряжен с риском оказаться в парадоксальной ситуации. Знание парадоксов голосования необходимо для предотвращения искажения демократического характера этой процедуры. Подчеркнем, что при любом из этих вариантов подразумевается отказ от принятия решения, если ни одна из альтернатив не получила необходимого процента голосов. Поскольку в реальной жизни отказ от дальнейших действий, следующих за решением, бывает недопустим, а переход к принятию за групповой выбор выбора отдельного лица (“диктатора”) – нежелательным, разрабатываются различные приемы, сокращающие число ситуаций, приводящих к отказу. Например, если два эксперта дали противоположные предпочтения между двумя вариантами a и b, то можно сделать выбор, сравнивая “силу предпочтения” каждого эксперта. При возможности введения количественного критерия оценки это сводится к арифметической операции, но и при порядковом сравнении есть возможность оценки “силы предпочтения”. В криминалистической практике в таких случаях экспертам предлагается в одном ряду с a и b упорядочить по предпочтению еще несколько альтернатив, скажем c, d и e. Пусть первый эксперт дал упорядочение (c, d, a, b, e), а второй – (b, c, d, e, a). Тогда можно сделать вывод, что степень предпочтения b по сравнению с a у второго эксперта больше, чем степень предпочтения a перед b у первого, и принять решение в пользу b (за этим приемом стоит ряд предположений – сравнимость интенсивностей предпочтений, одинаковая компетентность экспертов и т.д., требующих проверки в ответственных случаях) . Даже для консенсуса, требующего единогласия, разработаны приемы, облегчающие его достижение. Так, Р. Акофф отмечает: “Консенсус часто трудно достижим, но редко невозможен. Я обнаружил, что в трудных случаях очень эффективна следующая процедура. Первое – максимально уточнить формулировки альтернатив, между которыми консенсус не допускает выбора. Второе – коллективно построить тест эффективности альтернатив и принять консенсусом решение, что данный тест справедлив и что все согласны следовать его результату. Третье – провести тест и использовать его результат. Я смог успешно применить эту процедуру даже в таком случае, когда законодатели одного государства не могли прийти к согласию, вводить или нет смертную казнь за убийство. В результате обсуждения члены законодательного органа пришли к согласию, что они все имеют одну цель – минимизировать число жертв убийств. Как только такое согласие было достигнуто, проблема была сведена к конкретному вопросу: уменьшает ли введение смертной казни число убийств? Все согласились, что необходимо провести исследование, отвечающее на этот вопрос. Такое исследование было проведено и его результаты использованы (оно показало, что число убийств в ряде государств до и после отмены или введения смертной казни заметно и значимо не изменялось)” [44] . Если же не удавалось достичь консенсуса не только по поводу самих альтернатив, но и относительно способа их проверки, то, по мнению Акоффа, следует найти консенсусное решение, что же делать дальше. Интересно его наблюдение, что в таких случаях обычно принималось решение поручить выбор одному из авторитетных и ответственных лиц (мы еще вернемся к этому моменту). Фактически это переход от демократического, но не давшего решения правила голосования к недемократическому, но приводящему к какому-то решению “диктаторскому” принципу. Такое экспериментальное наблюдение имеет и теоретическое объяснение, излагаемое ниже на качественном уровне. ПАРАДОКСЫ ГОЛОСОВАНИЯ Итак, следующая особенность правила голосования – это возможность отказа от выбора из-за недостижения требуемого большинства. Казалось бы, исключив такую возможность, можно обеспечить принятие решения в любых случаях. Например, пусть три эксперта большинством голосов решают вопрос, какая из двух альтернатив более предпочтительна. При такой постановке вопроса они действительно не могут не сделать выбор. Однако здесь мы приходим к еще одной особенности правила голосования – его нетранзитивности. Пусть, например, каждая из трех группировок законодателей, образующих большинство лишь попарно, выдвинули свой вариант законопроекта: a, b и c. Или три парня заспорили, чья девушка лучше, и намереваются решить спор голосованием. Чтобы гарантировать большинство на каждом шаге процедуры, альтернативы предъявляются попарно. Каждая сторона руководствуется при этом своим набором предпочтений; пусть это соответственно последовательности (a > b > c), (b > c> a) и (c > a > b). После голосования по паре (a, b) в результате получаем два голоса против одного: a > b; по паре (b, c) имеем b > c; по паре (c, a) имеем c > a. Голосование большинством не привело к выяснению “общепризнанного” порядка альтернатив: a > b > c > a. В случае же применения процедуры, при которой после рассмотрения очередной пары отвергаемая альтернатива заменяется новой, окончательно принятое решение зависит от порядка предъявления альтернатив: при порядке (a, b, c) выбирается c; при порядке (b, c, a) выбор остановится на a; при порядке (a, c, b) – на b. Если таким образом принять законопроект, то чье мнение он будет выражать – большинства или организатора голосования? Очевидно, что такие решения не отвечают идеалу согласованного группового выбора. Причина данного парадокса нетранзитивности группового выбора состоит, конечно, в цикличности совокупности исходных индивидуальных предпочтений. Однако это лишь частный пример более общего явления, получившего название парадокса Эрроу (или теоремы о невозможности). Не вдаваясь в подробности этой теоремы и ее доказательства, изложим ее смысл. Из всевозможных функций F индивидуальных выборов R1, ..., Rn выделим те, которые отвечают требованиям, выражающим наше понимание того, какой выбор можно считать согласованным. Кроме формальных требований 10) “n 2”, “число альтернатив 3”, “F определена для любых {Ri}” естественно также потребовать, чтобы: 20) если в результате группового выбора предпочтение было отдано альтернативе x, то это решение не должно меняться, если кто-нибудь из ранее отвергавших x изменил свое предпочтение в его пользу (условие монотонности); 30) если изменения индивидуальных предпочтений не коснулись определенных альтернатив, то в новом групповом упорядочении порядок этих альтернатив не должен меняться (условие независимости несвязанных альтернатив); 40) для любой пары альтернатив x и y существует такой набор индивидуальных предпочтений, для которого F(R1, ..., Rn) = (x > y) (условие суверенности; без него возможно навязывание y независимо от порядков предпочтений индивидуумов); 50) не должно быть такого индивидуума, для которого из его предпочтения x > y (при любых x и y) вытекает, что F(R1, ..., Rn) = (x > y) независимо от предпочтений других индивидуумов (условие отсутствия диктаторства). Парадокс Эрроу состоит в том, что первые четыре условия противоречат пятому; не существует правила F, удовлетворяющего всем пяти требованиям. Анализ причин такого обескураживающего следствия из столь невинных на вид предположений показывает [21; 24], что основную роль играет возможность циклических множеств ранжирований, что характерно для бинарных отношений, удовлетворяющих условию 30. Нетранзитивность мажоритарного отношения может проявляться и в других неожиданных формах. Рассмотрим такую задачу [24]. Пусть каждый из n субъектов имеет свою долю ai общего ресурса Задачи группового выбора часто все же могут быть разрешены. Во-первых, в ряде случаев циклические ранжирования могут отсутствовать, либо они не охватывают “наиболее важные” альтернативы, либо принимаются меры по их обнаружению и устранению. Во-вторых, во многих случаях “диктаторский” принцип согласования не является неприемлемым. Это иллюстрируется примером оптимизации по “главному” из нескольких критериев. В других случаях это единственно возможный принцип (например, единоначалие в армии). В-третьих, переход (когда это возможно) к использованию единой числовой, а не порядковых индивидуальных шкал предпочтений может вообще аннулировать проблему нетранзитивности. В-четвертых, в реальных ситуациях мажоритарные правила применяются в комбинации с другими правилами, так что, образовав, например, коалицию, группы субъектов могут блокировать действие голосования. 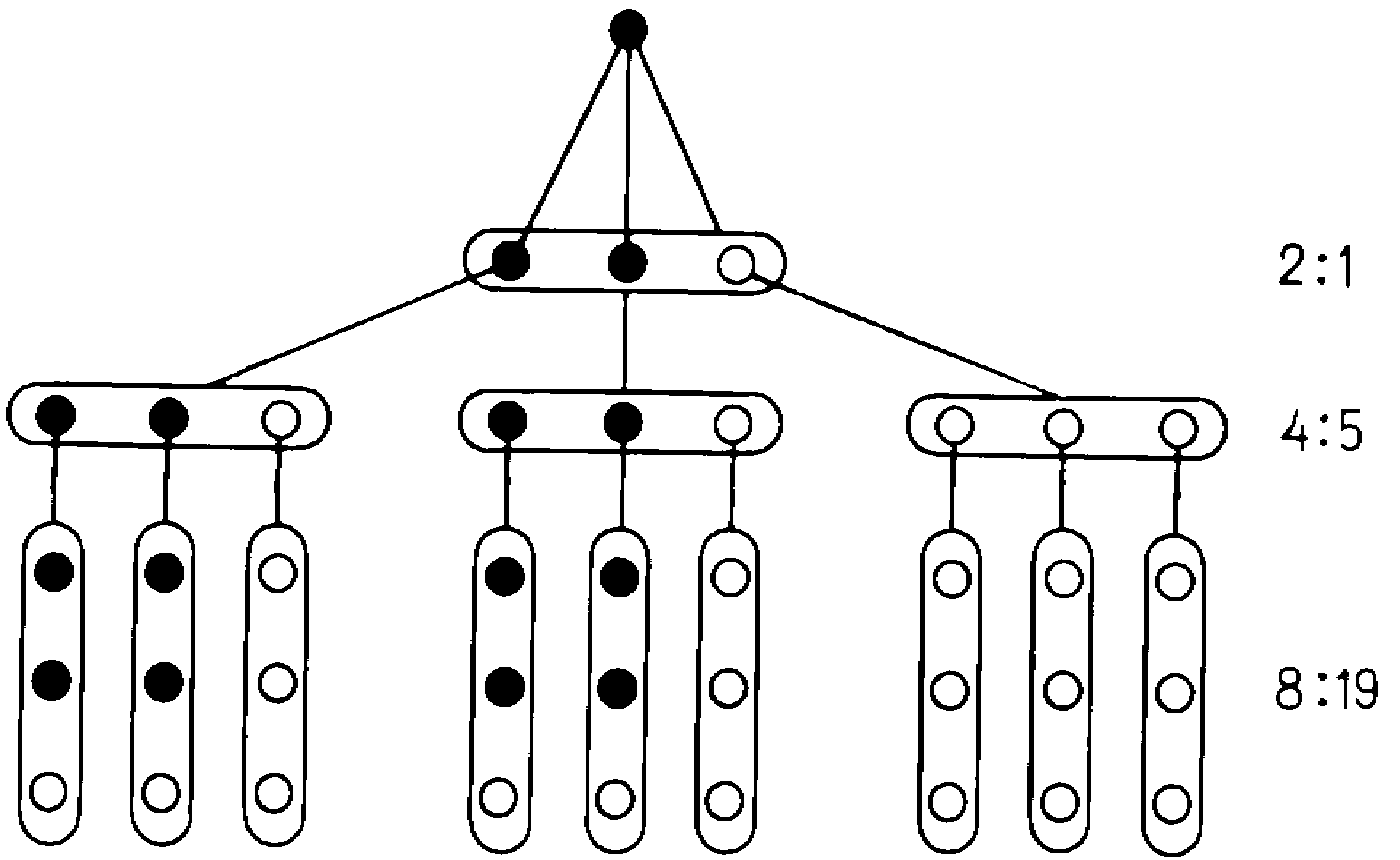 7.7 ————— Иллюстрация парадокса многоступенчатого голосования при наличии коалиции Здесь мы приходим к еще одной особенности голосования, которую следует иметь в виду на практике. Речь идет о вмешательстве коалиций в механизм голосования, фактически меняющем его характер. Например, при многоступенчатом голосовании по правилу большинства коалиция, находящаяся в меньшинстве, может добиться принятия своего решения. На рис. 7.7 изображено голосование по три большинством в 2/3 на каждой ступени. Видно, что уже на второй ступени меньшинство может навязывать свое мнение большинству. Если число ступеней не ограничивать, то теоретически побеждающее таким образом меньшинство может быть сколь угодно малым. То, что при многоступенчатом голосовании может победить кандидат, не набравший действительного большинства голосов, происходит и в действительности. Например, в 1876 г. президентом США был избран Р.Б. Хейес (185 голосов выборщиков), а не С. Дж. Тилден (184 голоса), хотя на долю последнего пришлось 51% голосов всех избирателей. Такие же ситуации имели место в президентских выборах 1874 и 1888 гг.
|
