отчет. Физика1. Перепишем уравнение плоскости в отрезках и изобразим пирамиду P x2y2z11
 Скачать 108.36 Kb.
|
|
1.8.1  1.8.2 Перепишем уравнение плоскости в отрезках и изобразим пирамиду:P: x2+y2+z1=1 1. Найдем поток векторного поля F через полную поверхность σ пирамиды V в направлении внешней нормали к ее поверхности непосредственно. Пσ=Пσ1+Пσ2+Пσ3+Пσ4, где Пσ1=ПABC, Пσ2=ПAOC, Пσ3=ПAOB, Пσ4=ПBOC. Пσ=ABCF,n10dσ+AOCF,n20dσ+AOBF,n30dσ+BOCF,n40dσ Вычислим каждый поверхностный интеграл Пσ1=ABCF,n10dσ, где n10- единичный вектор нормали, направленный вне пирамиды. Нормаль к плоскости x+y+2z-2=0 имеет координаты n=1;1;2. n=12+12+22=6, n10=16;16;26. γ=26>0⇒угол острый. dσ=dxdycosγ. Пσ1=ABCF,n10dσ=F=0;0;3x+y+2z; n10=16;16;26F,n10=263x+y+2z; dσ=62dxdy= =02dx02-x263x+y+2z62dy=02dx02-x3x+y+22-x-y2dy= =022x+2dx02-xdy=022x+22-xdx=202x+2-x2dx= =2x22+2x-x3302=26-83=203. На гранях АОС, АОВ, ВОС, соответственно z=0;y=0;x=0, а единичные векторы внешней нормали к этим граням, соответственно равны n20=0;0;-1, n30=0;-1;0, n40=-1;0;0. Пσ2=AOCF,n20dσ=z=0; F=0;0;3x+y+2z; n20=0;0;-1 F,n20=-3x+y; dσ=dxdy= =-02dx02-x3x+ydy=-02dx02-x3x+ydy=-023xy+y2202-xdx= =-024x+2-5x22dx=-2x2+2x-5x3602=-12+203=-163. Пσ3=AOBF,n30dσ=y=0; F=0;0;3x+y+2z; n30=0;-1;0 F,n30=0; dσ=dxdz=0. Пσ4=BOCF,n40dσ=x=0; F=0;0;3x+y+2z; n40=-1;0;0 F,n40=0; dσ=dydz=0. Пσ=Пσ1+Пσ2+Пσ3+Пσ4=203-163+0+0=43. Найдем поток по теореме Остроградского-Гаусса: Q=σF,ndσ=VdivFdxdydz Дивергенция: divF=∂P∂x+∂Q∂y+∂R∂z=∂∂x0+∂∂y0+∂∂z3x+y+2z=2≠0 П=VdivFdxdydz=2V=2∙13∙1∙12∙2∙2=43. 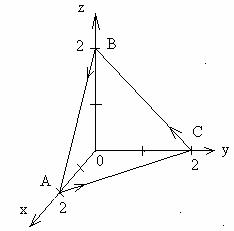 2.3.1 Решение: Векторы ř1, ř2, ř3, ř4 исходят из соответствующих зарядов q1,q2,q3,q4 и заканчиваются в центре квадрата 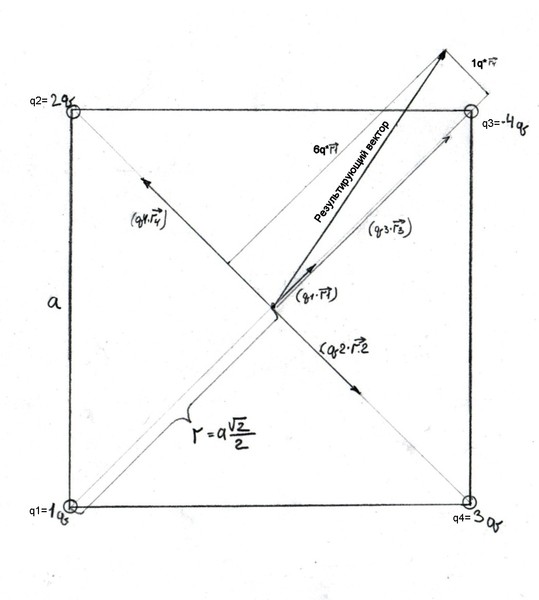 напряженность электростатического поля это вектор с направлением результирующего вектора и по модулю равен: |E| = q*√26 ř / ( 4π*ε0*ε*r³ ) ( q*√(26) ř ) это результирующий вектор, сначала складываем векторы вдоль каждой из диаганалей, и далее находим по теореме Пифагора. Его длина равна √(1²+5²)qr = √(26) qr; r сокращается и получается |E| = q*√26 / ( 4π*ε0*ε*r² ) ; r=a√(2)/2; |E| = q*4*√26 / ( 4*π* 8.85e-12 * 2 * a² ) = |E| = 91698775199 * q / a² (в/м) ; Находим потенциал: φ= (q1+q2+q3+q4)/ ( 4π*ε0*ε*r ) q1+q2+q3+q4 = 2q; r=a√(2)/2; φ== 2 *2q / ( 4*π* 8.85e-12 *a√(2) )= q / (a*π* 8.85e-12 *√(2) ) ; φ=25432664298 * q / a (в) 2.3.2 Решение: 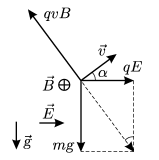 После того, как частица начала двигаться в области пространства, в которой есть только поле g⃗ g→, её скорость начала уменьшаться. Это означает, что скорость частицы имеет составляющую, направленную противоположно вектору g⃗ g→, то есть частица движется «вверх» по отношению к полю силы тяжести. Следовательно, векторы E⃗ ,B⃗ ,g⃗ E→,B→,g→ скорость частицы v⃗ v→ и действующие на неё электрическая, магнитная и гравитационная силы направлены так, как показано на рисунке. Угол к горизонту, под которым частица двигалась, находясь во всех трёх полях, может быть найден из условия равенства нулю суммы действующих на неё сил: 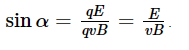 После попадания в ту область пространства, где есть только поле силы тяжести, частица будет двигаться по параболе. Её скорость будет минимальна в верхней точке траектории, тогда, когда вертикальная составляющая скорости обратится в ноль. Это произойдёт через время  3.3.1 Решение Объем сердечника V=mmρm Максимальная запасенная энергия Wmax=Bm22μμ0V=Bm22μμ0∙mmρm Подсчитаем Wm=1,922∙190∙4∙π∙10-7∙37900=2,872 (Дж) Ответ: Энергия, запасенная сердечником 2,872 Дж 3.3.2 Решение: В диэлектрике создано равномерное электрическое поле Е=2,5 E=2,5  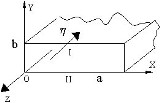+1,7 +9,2 . Вектор электрической индукции  и угол в пространстве между векторами  и :• =ε0(16,25 +11,05 +61,18 ), ∠ ( * )=6,59*10-3 рад |