Практическая работа №3,4 по информ. Практическая работа №3,4 по Информатике и ИКТ. Перевод чисел и арифметические действия в позиционных системах счисления

• Название: Перевод чисел и арифметические действия в позиционных системах счисления
• Анкор: Практическая работа №3,4 по информ
• Дата: 18.11.2022
• Размер: 54.32 Kb.
• Имя файла: Практическая работа №3,4 по Информатике и ИКТ.docx
• Тип: Практическая работа; #795594

Практическая работа №3,4

Тема: Перевод чисел и арифметические действия в позиционных системах счисления.

Цель работы: научиться представлять числа в различных системах счисления, научиться выполнять арифметические действия в различных системах счисления.

Студент должен

знать:

• 
  принципы представления чисел в позиционных и непозиционных системах счисления;
  
• 
  правила выполнения арифметических операций в позиционных системах счисления;
  

уметь:

• 
  переводить числа из одной системы счисления в другую.
  

Теоретическое обоснование.

1. Система счисления.

Система счисления — это совокупность приемов и правил, по которым числа записываются и читаются.

Существуют позиционные и непозиционные системы счисления.

В непозиционных системах счисления вес цифры (т. е. тот вклад, который она вносит в значение числа) не зависит от ее позиции в записи числа. Так, в римской системе счисления в числе ХХХII (тридцать два) вес цифры Х в любой позиции равен просто десяти.

В позиционных системах счисления вес каждой цифры изменяется в зависимости от ее положения (позиции) в последовательности цифр, изображающих число. Например, в числе 757,7 первая семерка означает 7 сотен, вторая — 7 единиц, а третья — 7 десятых долей единицы.

Любая позиционная система счисления характеризуется своим основанием.
Основание позиционной системы счисления — количество различных цифр, используемых для изображения чисел в данной системе счисления.

В каждой системе счисления цифры упорядочены в соответствии с их значениями:

1 больше 0, 2 больше 1 и т.д.

      Продвижением цифры называют замену её следующей по величине.

Целые числа в любой системе счисления порождаются с помощью Правила счета.
  Для образования целого числа, следующего за любым данным целым числом, нужно продвинуть самую правую цифру числа; если какая-либо цифра после продвижения стала нулем, то нужно продвинуть цифру, стоящую слева от неё.

Применяя это правило, запишем первые десять целых чисел

• 
  в двоичной системе:         0,   1,   10,   11,   100,   101,   110,   111,   1000,   1001;
  
• 
  в восьмеричной системе: 0,   1,   2,   3,   4,   5,   6,   7,   10,   11.
  

2. Системы счисления, используемые специалистами для общения с компьютером

Кроме десятичной широко используются системы с основанием, являющимся целой степенью числа 2, а именно:

• 
  двоичная (используются цифры 0, 1);
  
• 
  восьмеричная (используются цифры 0, 1, ..., 7);
  
• 
  шестнадцатеричная (для первых целых чисел от нуля до девяти используются цифры 0, 1, ..., 9, а для следующих чисел — от десяти до пятнадцати — в качестве цифр используются символы A, B, C, D, E, F).
  

Полезно запомнить запись в этих системах счисления первых двух десятков целых чисел:

10-я 2-я 8-я 16-я 0 0 0 0 1 1 1 1 2 10 2 2 3 11 3 3 4 100 4 4 5 101 5 5 6 110 6 6 7 111 7 7 8 1000 10 8 9 1001 11 9

10-я 2-я 8-я 16-я 10 1010 12 A 11 1011 13 B 12 1100 14 C 13 1101 15 D 14 1110 16 E 15 1111 17 F 16 10000 20 10 17 10001 21 11 18 10010 22 12 19 10011 23 13

Из всех систем счисления особенно проста и поэтому интересна для технической реализации в компьютерах двоичная система счисления.

Перевод чисел из десятичной системы в двоичную и наоборот выполняет машина. Однако, чтобы профессионально использовать компьютер, следует научиться понимать слово машины. Для этого и разработаны восьмеричная и шестнадцатеричная системы.

Числа в этих системах читаются почти так же легко, как десятичные, требуют соответственно в три (восьмеричная) и в четыре (шестнадцатеричная) раза меньше разрядов, чем в двоичной системе (ведь числа 8 и 16 — соответственно, третья и четвертая степени числа 2).
3. Перевод целого число из десятичной системы в любую другую позиционную систему счисления.

Для перевода целого десятичного числа  N  в систему счисления с основанием  q  необходимо  N  разделить с остатком ("нацело") на  q , записанное в той же десятичной системе. Затем неполное частное, полученное от такого деления, нужно снова разделить с остатком на  q , и т.д., пока последнее полученное неполное частное не станет равным нулю. Представлением числа N  в новой системе счисления будет последовательность остатков деления, изображенных одной q-ичной цифрой и записанных в порядке, обратном порядку их получения.

Пример: Переведем число 75 из десятичной системы в двоичную, восьмеричную и шестнадцатеричную:

7 5 2

1 37 2

1 18 2_

0 9 2

1 4 2

0 2 2

0 1

75₁₀=1001011₂



75 8

3 9 8

1 1



75₁₀=113₈

75 16

11 _4
75₁₀=43₁₆

Ответ: 75₁₀ = 1 001 011₂   =  113₈  =  4B₁₆.

4. Перевод числа из двоичной (восьмеричной, шестнадцатеричной) системы в десятичную.

Перевод в десятичную систему числа x, записанного в q-ичной системе счисления (q = 2, 8 или 16) в виде x_q = (a_na_n-1   ...  a₀  ,  a_-1  a_-2   ...   a_-m)_q   сводится к вычислению значения многочлена 

x₁₀ = a_n  qⁿ +  a_n-1  q^n-1   +   ...   +  a₀   q⁰   +   a_-1   q ^-1   +   a_-2   q^-2   +     ...     +   a_-m   q^-m    
средствами десятичной арифметики. 

Примеpы:

1. 
   Переведем число 10011,0101 из двоичной системы в десятичную.
   

10011₂=1*2⁴+0*2³+0*2²+1*2¹+1*2⁰ =19₁₀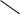

2. 
   П ереведем число 105,12₈ из восьмеричной системы в десятичную.
   

105₈=1*8²+0*8¹+5*8⁰=69₁₀

3. 
   Переведем число А5,Е2₁₆ из шестнадцатеричной системы в десятичную.
   

А5₁₆=А*16¹+5*16⁰=10*16+5*1=165
5. Выполнение арифметических действий в разных системах счисления.

Рассмотрим основные арифметические операции: сложение, вычитание. Правила выполнения этих операций в десятичной системе хорошо известны — это сложение, вычитание, умножение столбиком   и  деление углом. Эти правила применимы и ко всем другим позиционным системам счисления. Только таблицами сложения и умножения надо пользоваться особыми для каждой системы.

• С л о ж е н и е. Таблицы сложения легко составить, используя Правило Счета.

При сложении цифры суммируются по разрядам, и если при этом возникает избыток, то он переносится влево.

Сложение в двоичной системе



    Сложение в восьмеричной системе

Сложение в шестнадцатеричной системе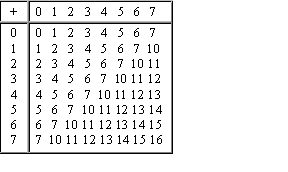



   

Пример 1. Сложим числа 15 и 6 в различных системах счисления.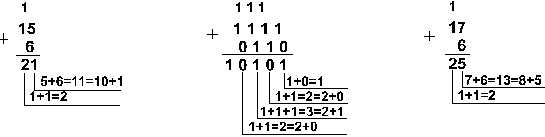


     

Шестнадцатеричная: F₁₆+6₁₆



Ответ: 15+6 = 21₁₀ = 10101₂ = 25₈ = 15₁₆. 
  Пример 2. Сложим числа 15, 7 и 3.





Шестнадцатеричная: F₁₆+7₁₆+3₁₆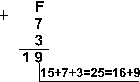



Ответ: 5+7+3 = 25₁₀ = 11001₂ = 31₈ = 19₁₆. 
  Пример 3. Сложим числа 141,5 и 59,75.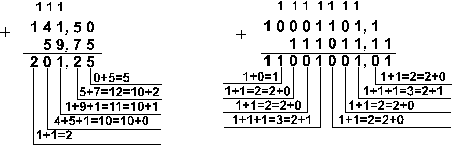








 
Ответ: 141,5 + 59,75 = 201,25₁₀ = 11001001,01₂ = 311,2₈ = C9,4₁₆

Ход работы:

1. 
   Рассмотреть предложенные примеры;
   
2. 
   Выполнить практическое задание по вариантам;
   
3. 
   Оформить отчет.
   
4. 
   Ответить на контрольные вопросы по указанию преподавателя.
   

Практические задания:

Вариант 1.

Задание 1.

Переведите числа в десятичную систему

 а) 1011011₂ б) 517₈; в) 1F₁₆; 

Задание 2.

Переведите число из десятичной системы в двоичную, восьмеричную и шестнадцатеричную

259₁₀;   

Задание 3.

Сложите числа, а Переведите числа в десятичную систему, а затем проверьте результаты, выполнив обратные переводы">затем проверьте результаты, выполнив соответствующие десятичные сложения:
а) 1011101₂ и 1110111₂; б) 437₈ и 675₈; в) 5A1₁₆ и 27F₁₆;

Задание 4.

Вычтите:

а) 10100₂-111₂ б) 230₈- 155₈ в) 31₁₆- 1А₁₆
Вариант 2.

Задание 1.

Переведите числа в десятичную систему, а затем проверьте результаты, выполнив обратные переводы

а) 10110111₂; б) 1010₈;  в) ABC₁₆; 

Задание 2.

Переведите число из десятичной системы в двоичную, восьмеричную и шестнадцатеричную, а затем проверьте результаты, выполнив обратный перевод

429₁₀;

Задание 3.

Сложите числа, а затем проверьте результаты, выполнив соответствующие десятичные сложения:

а) 1011101₂ и 101011₂; б) 165₈ и 37₈; в) 1А9₁₆ и 2ВC₁₆;

Задание 4.

Вычтите:

а) 1101₂-1011₂ из б) 102₈-47₈ в) 2А30₁₆- F9E₁₆

Вариант 3.

Задание 1. Переведите числа в десятичную систему, а затем проверьте результаты, выполнив обратные переводы:

а) 11100001₂; б) 1234₈; в) 1010₁₆;

Задание 2.

Переведите число из десятичной системы в двоичную, восьмеричную и шестнадцатеричную, а затем проверьте результаты, выполнив обратный перевод

881₁₀;     

Задание 3.

Сложите числа, а затем проверьте результаты, выполнив соответствующие десятичные сложения:

а) 10111₂ и 11011₂; б) 575₈ и 146₈; в) A5B₁₆ и E7F₁₆;

Задание 4.

Вычтите:

а) 10010₂-1111₂ б) 567₈ -101₈; в) B92₁₆-19F₁₆
Вариант 4.

Задание 1. Переведите числа в десятичную систему, а затем проверьте результаты, выполнив обратные переводы:

а) 1000110₂; б) 34₈; в) А4₁₆;

Задание 2.

Переведите число из десятичной системы в двоичную, восьмеричную и шестнадцатеричную, а затем проверьте результаты, выполнив обратный перевод

372₁₀

Задание 3.

Сложите числа, а затем проверьте результаты, выполнив соответствующие десятичные сложения:

а) 1011111₂ и 110101₂; б) 617₈ и 407₈; в)2 E9₁₆ и 5F₁₆.

Задание 4.

Вычтите:

а) 111011₂- 10001₂ б) 3001₈-1654₈ в)5678₁₆- ABC₁₆
Вариант 5.

Задание 1. Переведите числа в десятичную систему, а затем проверьте результаты, выполнив обратные переводы:

а) 11010011₂; б) 1231₈; в) 1DE₁₆.

Задание 2.

Переведите число из десятичной системы в двоичную, восьмеричную и шестнадцатеричную, а затем проверьте результаты, выполнив обратный перевод

612₁₀.

Задание 3.

Сложите числа, а затем проверьте результаты, выполнив соответствующие десятичные сложения:

а)1100101₂ и 11010₂ б)562₈ и 127₈ и) А12₁₆ и FDA₁₆

Задание 4.

Вычтите:

а) 10100₂-1101₂ б)123₈-56₈ в)A2D₁₆-17F₁₆
 

Содержание отчета:

1. 
   Название и цель работы.
   
2. 
   Результат выполнения практических заданий.
   
3. 
   Ответы на контрольные вопросы по указанию преподавателя.
   

Контрольные вопросы.

1. 
   Какие системы счисления вы знает?
   
2. 
   В чем особенности двоичной системы счисления?(Таблица)
   
3. 
   В чем особенности восьмеричной системы счисления? (Таблица)
   
4. 
   В чем особенности шестнадцатеричной системы счисления? (Таблица)
   
5. 
   Как осуществляется связь между «2», «8», «16» системами счисления?
   
6. 
   Как перевести целое десятичное число в «2», «8», «16» системы счисления?
   
7. 
   Как перевести число из «2», «8», «16» системы счисления в десятичную систему счисления? Покажите на примере.
   

Литература

1. 
   Бешенков С.А., Ракитина Е.А. Информатика. Учебник 10 кл. – М., 2010.
   
2. 
   Михеева Е.В. Практикум по информации: учеб. пособие. – М., 2014.
   
3. 
   Михеева Е.В., Титова О.И. Информатика: учебник. – М., 2010.
   
4. 
   Угринович Н.Д. Информатика и информационные технологии. Учебник 10–11 кл. – М., 2010.