Контрольная работа № 1 по информатике Тема: «Перевод чисел из одной позиционной системы счисления в другую». Контрольная работа 1. Перевод чисел из одной позиционной системы счисления в другую
 Скачать 143.28 Kb. Скачать 143.28 Kb.
|
|
Задание 9. Заданы две логические функции 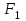 и и 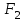 . Путем тождественных преобразований получите минимальную форму записи функций и проверьте, является ли функция . Путем тождественных преобразований получите минимальную форму записи функций и проверьте, является ли функция 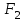 тождественной функции тождественной функции 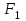 . .1. 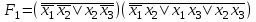 ; ;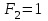 на наборах 0, 4 на наборах 0, 4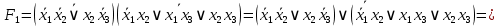 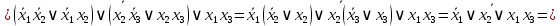 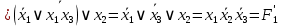 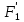 является минимальной формой является минимальной формой 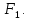 Упростим СДНФ функции 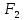 : :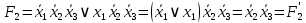 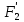 является минимальной формой является минимальной формой 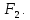 Заметим, что 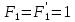 только на наборе только на наборе 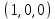 (набор 4). Следовательно, (набор 4). Следовательно, 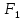 не равна тождественно не равна тождественно 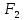 . .2. 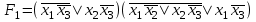 ; ;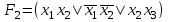 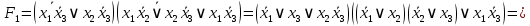 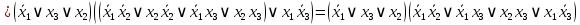 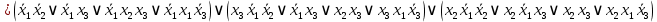 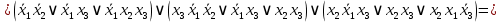 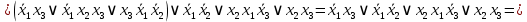 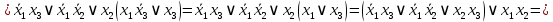 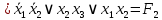 Следовательно, 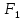 равна тождественно равна тождественно 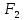 . .3. 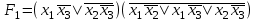 ; ;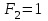 на наборах 0, 1, 3, 7 на наборах 0, 1, 3, 7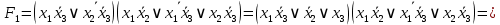 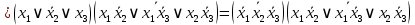 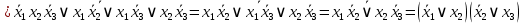 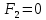 на наборах 2, 4, 5, 6. Упрощаем СКНФ: на наборах 2, 4, 5, 6. Упрощаем СКНФ: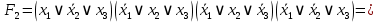 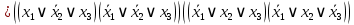 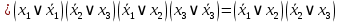 Следовательно, 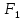 равна тождественно равна тождественно 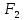 . .Задание 10. Найти формулу, определяющую функцию Ф(x,y,z), по заданной таблице истинности:
Функция принимает ложное значение на наборах: 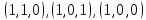 Им соответствуют следующие элементарные дизъюнкции: 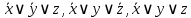 Тогда совершенная конъюнктивная форма получается объединением этих дизъюнкций с помощью операции конъюнкции: 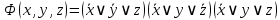 Задание 11. По таблицам истинности найдите формулы, определяющие функции F1(x,y,z), F2(x,y,z), F3(x,y,z), F4(x,y,z) и придайте им более простой вид:
1. Функция 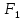 принимает истинное значение на наборах: принимает истинное значение на наборах: 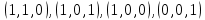 Им соответствуют следующие элементарные конъюнкции: 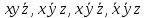 Тогда совершенная дизъюнктивная форма получается объединением этих конъюнкций с помощью операции дизъюнкции: 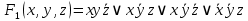 Упростим эту формулу 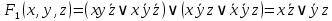 2. Функция 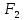 принимает истинное значение на наборах: принимает истинное значение на наборах: 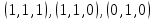 Им соответствуют следующие элементарные конъюнкции: 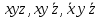 Тогда СДНФ 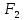 равна: равна: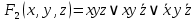 Упростим эту формулу 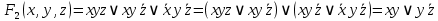 3. Функция 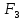 принимает истинное значение на наборах: принимает истинное значение на наборах: 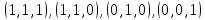 Им соответствуют следующие элементарные конъюнкции: 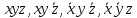 Тогда СДНФ 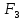 равна: равна: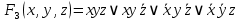 Упростим эту формулу 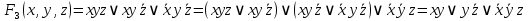 4. Функция 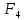 принимает истинное значение на наборах: принимает истинное значение на наборах: 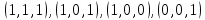 Им соответствуют следующие элементарные конъюнкции: 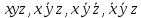 Тогда СДНФ 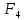 равна: равна: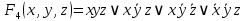 Упростим эту формулу 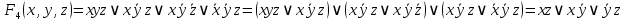 Задание 12. Докажите равносильность формул 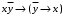 и и 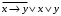 сравнением их совершенных нормальных форм (конъюнктивных или дизъюнктивных) 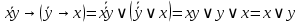 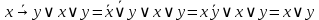 Так как совершенные конъюнктивные нормальный формы совпадают, то формулы 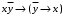 и и 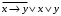 равносильны. равносильны.Задание 13. Определите корень Х = F(А,В) логического уравнения 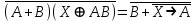 Пусть 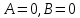 . Тогда уравнение при данных . Тогда уравнение при данных 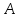 и и 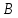 преобразуется преобразуется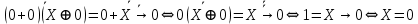 Пусть 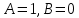 . Тогда . Тогда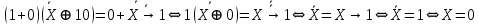 Пусть 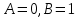 . Тогда . Тогда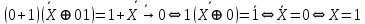 Пусть 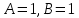 . Тогда . Тогда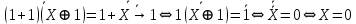 Следовательно, 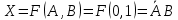 . . |
