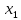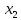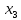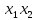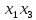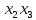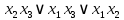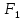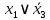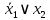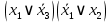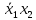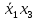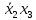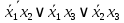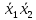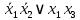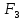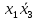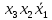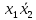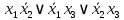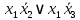Контрольная работа № 1 по информатике Тема: «Перевод чисел из одной позиционной системы счисления в другую». Контрольная работа 1. Перевод чисел из одной позиционной системы счисления в другую
 Скачать 143.28 Kb. Скачать 143.28 Kb.
|
|
Задание 4: Применяя таблицы истинности, докажите тождественную истинность логических формул: 1. 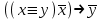 ; ;
2. 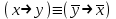 ; ;
3 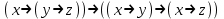 . .
Так как в последних столбца таблиц истинности все единицы, то тождественная истинность выражений доказана. Задание 5. Проверить, не составляя таблицы истинности, являются ли следующие логические формулы тождественно ложными (противоречиями). 1. 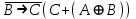 2. 2. 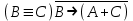 3. 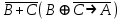 4. 4. 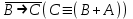 5. 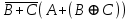 Решение: 1. 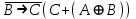 Конъюнкция истинна тогда и только тогда, когда оба слагаемых истины. Следовательно, 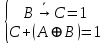 Из первого уравнения системы следует, что 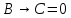 . Импликация принимает значение ложь только при . Импликация принимает значение ложь только при 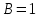 и и 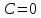 . .Подставляем во второе уравнение 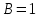 и и 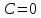 и упрощаем его: и упрощаем его: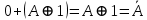 Получаем, что 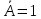 и, следовательно, и, следовательно, 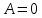 . То есть, при . То есть, при 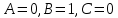 данная формула принимает истинное значение. Следовательно, она не является тождественно ложной. данная формула принимает истинное значение. Следовательно, она не является тождественно ложной.2. 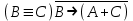 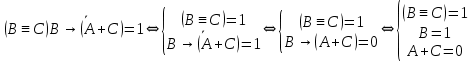 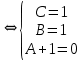 Уравнение 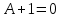 не имеет решения, так как не имеет решения, так как 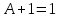 при любом при любом 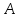 . Следовательно, и исходно уравнение не имеет решения, и данная формула является противоречием. . Следовательно, и исходно уравнение не имеет решения, и данная формула является противоречием.3. 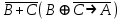 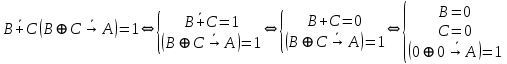 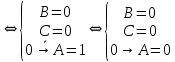 Уравнение 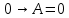 не имеет решения, так как не имеет решения, так как 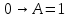 при любом при любом  . Следовательно, и исходно уравнение не имеет решения, и данная формула является противоречием. . Следовательно, и исходно уравнение не имеет решения, и данная формула является противоречием.4. 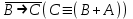 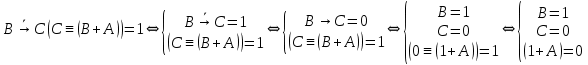 Уравнение 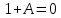 не имеет решения, так как не имеет решения, так как 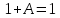 при любом при любом 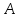 . Следовательно, и исходно уравнение не имеет решения, и данная формула является противоречием. . Следовательно, и исходно уравнение не имеет решения, и данная формула является противоречием.5. 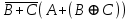 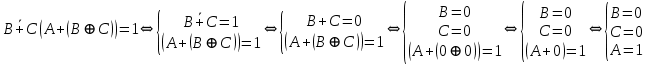 То есть, при 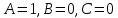 данная формула принимает истинное значение. Следовательно, она не является тождественно ложной. данная формула принимает истинное значение. Следовательно, она не является тождественно ложной.Задание 6. Проверить, не составляя таблицы истинности, являются ли следующие логические формулы тождественно истинными (тавтологиями). 1. 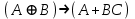 2. 2. 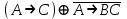 3. 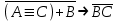 4. 4. 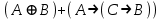 Решение: 1. 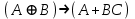 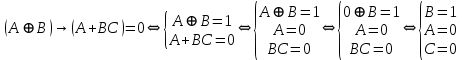 То есть, при 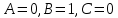 данная формула принимает ложное значение. Следовательно, она не является тождественно истинной. данная формула принимает ложное значение. Следовательно, она не является тождественно истинной.2. 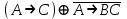 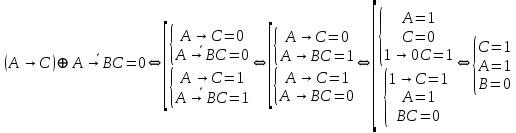 То есть, при 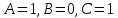 данная формула принимает ложное значение. Следовательно, она не является тождественно истинной. данная формула принимает ложное значение. Следовательно, она не является тождественно истинной.3. 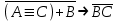 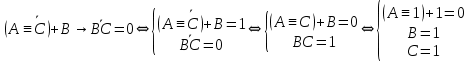 Уравнение 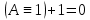 не имеет решения, так как не имеет решения, так как 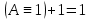 при любом при любом 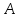 . Следовательно, и исходно уравнение не имеет решения, и данная формула является тавтологией. . Следовательно, и исходно уравнение не имеет решения, и данная формула является тавтологией.4. 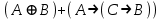 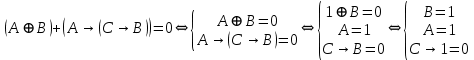 Уравнение 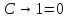 не имеет решения, так как не имеет решения, так как 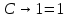 при любом при любом  . Следовательно, и исходно уравнение не имеет решения, и данная формула является тавтологией. . Следовательно, и исходно уравнение не имеет решения, и данная формула является тавтологией.Задание 7. Упростить формулу 1. 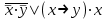 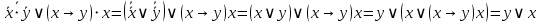 2. 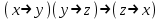 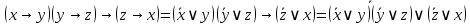 = =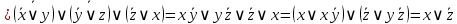 3. 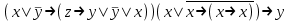 1) 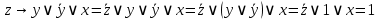 2) 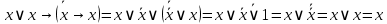 3) 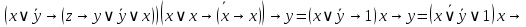 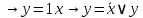 Задание 8. Используя известные правила тождественных преобразований, упростите логические функции и покажите эквивалентность преобразованной функции исходной: 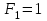 на наборах 3, 5, 6, 7; на наборах 3, 5, 6, 7;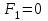 на наборах 1, 3, 4, 5; на наборах 1, 3, 4, 5;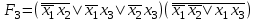 ; ;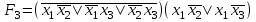 ; ;Решение: 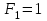 на наборах 3, 5, 6, 7; на наборах 3, 5, 6, 7;Функция принимает истинное значение на наборах: 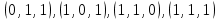 Им соответствуют следующие элементарные конъюнкции: 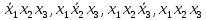 Тогда совершенная дизъюнктивная форма получается объединением этих конъюнкций с помощью операции дизъюнкции: 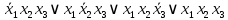 Упростим эту формулу 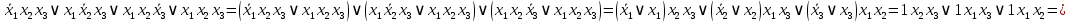 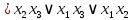 Для проверки эквивалентности построим таблицу истинности обоих функций и убедимся, что столбцы значений совпадают:
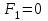 на наборах 1, 3, 4, 5; на наборах 1, 3, 4, 5;Функция принимает ложное значение на наборах: 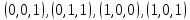 Им соответствуют следующие элементарные дизъюнкции: 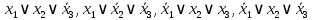 Тогда совершенная конъюнктивная форма получается объединением этих дизъюнкций с помощью операции конъюнкции: 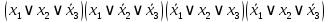 Упростим эту формулу 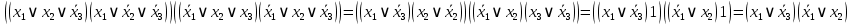 Для проверки эквивалентности построим таблицу истинности обоих функций и убедимся, что столбцы значений совпадают:
3. 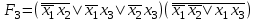 ; ;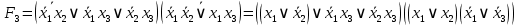 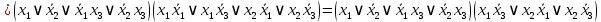 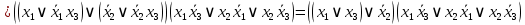 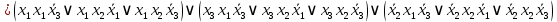 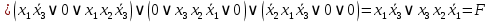 Для проверки эквивалентности построим таблицу истинности обоих функций и убедимся, что столбцы значений совпадают:
4. 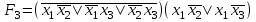 ; ;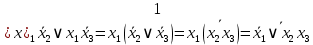 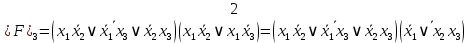 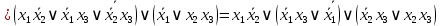 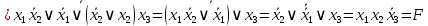 Для проверки эквивалентности построим таблицу истинности обоих функций и убедимся, что столбцы значений совпадают:
|

 Y
Y