Метод дихотомии. Метод Дихотомии Семенов Андрей. Пермский национальный исследовательский политехнический университет Кафедра Информационные технологии и автоматизированные системы
 Скачать 0.64 Mb. Скачать 0.64 Mb.
|
|
Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования «Пермский национальный исследовательский политехнический университет» Кафедра «Информационные технологии и автоматизированные системы» О Т Ч Ё Т По лабораторной работе Приближенное вычисление корней функции методом дихотомии Дисциплина: основы алгоритмизации и программирования. Семестр 1. Выполнил работу студент группы РИС-21-1б Семенов Андрей Олегович Проверил Доцент кафедры ИТАС Полякова Ольга Андреевна Пермь – 2021 Постановка задачи Требуется реализовать алгоритм нахождения корней нелинейного уравнения методом дихотомии (метод половинного деления). Анализ задачи 1. Описание метода 1.1. Пусть нелинейная функция вида 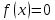 имеет один единственный корень на отрезке имеет один единственный корень на отрезке 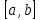 . .1.2 Тогда абсцисса 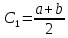 делит отрезок делит отрезок 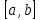 на две части: на две части: 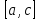 и и 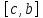 . .1.3 Следующим шагом является переопределение исходного отрезка 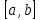 , таким образом, чтобы корень находился на этом отрезке. Иными словами, из двух отрезков , таким образом, чтобы корень находился на этом отрезке. Иными словами, из двух отрезков 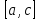 и и 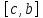 , требуется выбрать такой, чтобы функция меняла свой знак. Выбранный отрезок сделать основным. , требуется выбрать такой, чтобы функция меняла свой знак. Выбранный отрезок сделать основным.1.3 Данное действие по делению отрезка и отсеиванию повторять до тех пор, пока не выполнится критерий останова. 1.4 Критерии останова: 1) С каждым новым шагом длина отрезка постоянно уменьшается, что может служить критерием останова: 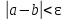 , где , где 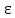 заданная точность. заданная точность.2)С каждым новым шагом оба конца отрезка приближаются к корню. Таким образом, значение функции на концах отрезка приближается к нулю: 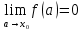 или или 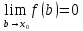 где где 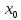 – искомое значение корня. Значение функции на концах отрезка должно мало отличатся от нуля. Получается, что критерием останова служат выражения – искомое значение корня. Значение функции на концах отрезка должно мало отличатся от нуля. Получается, что критерием останова служат выражения 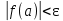 или или 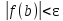 . .2. Описание алгоритма 2.1 Необходимо получить от пользователя функцию (полином) вида 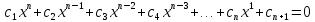 , где , где 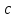 – коэффициент при независимой переменной, – коэффициент при независимой переменной, 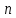 – старшая степень при независимой переменной, – старшая степень при независимой переменной, 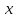 – независимая переменная. – независимая переменная. 2.1.1 Важными константами здесь являются nи c. Эти константы необходимо получить от пользователя. 2.1.2 Также необходимо динамически освобождать память под полиномиальные коэффициенты. Если n – старшая степень независимой переменной, то объем выделяемой памяти – 8*(n+1) байт. Умножаю на 8, т.к полиномиальные коэффициенты будут иметь вещественный тип double. 2.1.2 Необходимо предоставить пользователю выбор: считать данные с файла или ввести вручную. 2.2 Необходима функция, которая по заданным значениям nи cнаходит значение функции в точке 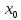 . Эта функция будет работать следующим образом: на вход получает массив из коэффициентов при . Эта функция будет работать следующим образом: на вход получает массив из коэффициентов при 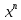 , получает старшую степень при независимой переменной, локальной переменной вещественного типа doubleresult присваивает значение коэффициента при старшей степени аргумента функции. Далее в итерационном цикле, nраз переменной result присваивает значение result*arg +coeffs[i+1], где arg вычисляемое значение функции, coeffs- массив из коэффициентов. Получается следующие выражение: , получает старшую степень при независимой переменной, локальной переменной вещественного типа doubleresult присваивает значение коэффициента при старшей степени аргумента функции. Далее в итерационном цикле, nраз переменной result присваивает значение result*arg +coeffs[i+1], где arg вычисляемое значение функции, coeffs- массив из коэффициентов. Получается следующие выражение: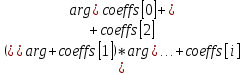 Далее функция возвращает полученное значение функции в точке arg. Далее функция возвращает полученное значение функции в точке arg.2.3 Следующим шагом является получение значений начала и конца промежутка, а также необходимой пользователю точности. 2.4 Нужна проверка на знакопеременность функции на заданном отрезке. Проверка на знакопеременность осуществляется следующим образом: 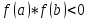 . a и b – абсциссы начала и конца отрезка соответственно. . a и b – абсциссы начала и конца отрезка соответственно.2.4.1 Если проверка успешна, то переходим к шагу 2.5 2.4.2 Если вводимая пользователем функция не удовлетворяет проверке, то необходимо вывести сообщение о том, что функция не имеет корней на заданном интервале, или имеет более одного корня. 2.5 Далее в поисковом цикле, пока не достигнута заданная точность или среднее значение не является корнем уравнения, необходимо находить середину интервала 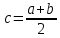 , переопределять отрезок [a, b], основываясь на свойствах знакопеременности функции. Корень находится на отрезке, если значение функции в разных концах отрезка отличны по знаку. , переопределять отрезок [a, b], основываясь на свойствах знакопеременности функции. Корень находится на отрезке, если значение функции в разных концах отрезка отличны по знаку.2.6 Таким образом через некоторое количество шагов, значение функции на концах отрезка, примет близкое к нулю значение. Будет достигнута заданная точность. 2.7 После уточнения корня с заданной точностью, необходимо вывести одно из значений начала или конца отрезка, удалить освобожденную память под полиномиальные коэффициенты и завершить работу программы. Используемые переменные boolfrom_file = 0; флаг, который включается, если пользователь решает считать все данные с файла. boolfx_null_average = false; - флаг, который включается, если середина отрезка является корнем уравнения. double *coeffs; - указатель на начало массива, где хранятся полиномиальные коэффициенты, получаемые от пользователя. intn; - старшая степень при независимой переменной. doublestart; - начало отрезка doubleaverage; - среднее значение doubleend_x; - конец промежутка double epsilon; - точность Блок-схема  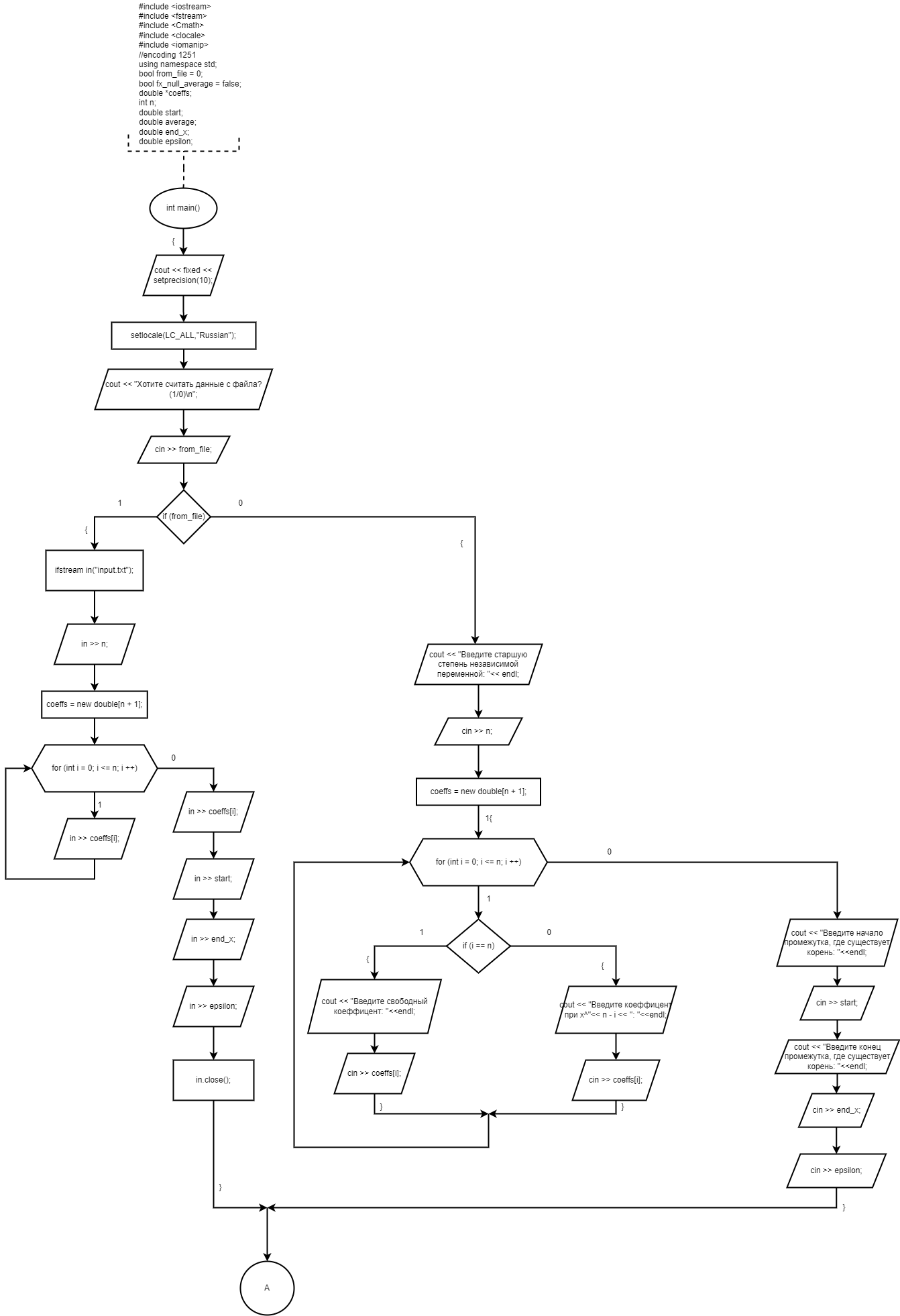 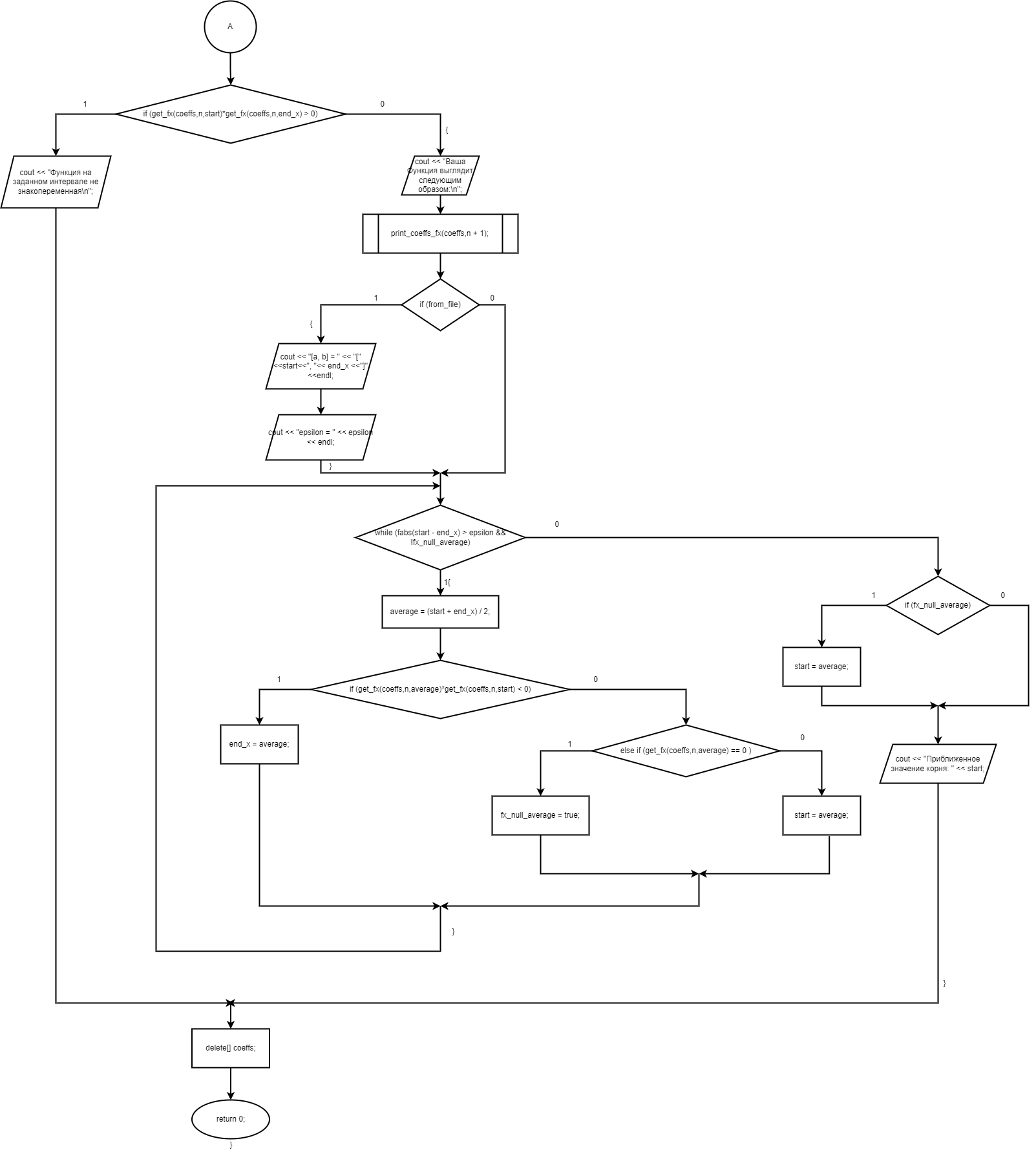 Код на языке С++ #include #include #include #include #include //encoding 1251 using namespace std; double get_fx(double *coeffs, int n, double arg) { double result = coeffs[0]; for (int i = 0; i < n; i ++) { result = result * arg + coeffs[i+1]; } return result; } void print_coeffs_fx(double *coeffs,int n,char end_of_output = '\n') { for (int i = 0; i < n; i++) { if (i != n - 1) { if (coeffs[i] != 0) { if( i != 0) { if(coeffs[i] > 0) { cout << '+'; } } cout << coeffs[i]<<"x^" < } } else { if (coeffs[i] != 0) { cout << coeffs[i]; } } } cout << " = 0"< } bool from_file = 0; bool fx_null_average = false; double *coeffs; int n; double start; double average; double end_x; double epsilon; int main() { cout << fixed << setprecision(10); setlocale(LC_ALL,"Russian"); cout << "Хотите считать данные с файла? (1/0)\n"; cin >> from_file; if (from_file) { ifstream in("input.txt"); in >> n; coeffs = new double[n + 1]; for (int i = 0; i <= n; i ++) { in >> coeffs[i]; } in >> start; in >> end_x; in >> epsilon; in.close(); } else { cout << "Введите старшую степень независимой переменной: "<< endl; cin >> n; coeffs = new double[n + 1]; for (int i = 0; i <= n; i ++) { if (i == n) { cout << "Введите свободный коеффицент: "< cin >> coeffs[i]; } else { cout << "Введите коеффицент при x^"<< n - i << ": "< cin >> coeffs[i]; } } cout << "Введите начало промежутка, где существует корень: "< cin >> start; cout << "Введите конец промежутка, где существует корень: "< cin >> end_x; cout << "Введите точность: "< cin >> epsilon; } if (get_fx(coeffs,n,start)*get_fx(coeffs,n,end_x) > 0) { cout << "Функция на заданном интервале не знакопеременная\n"; } else { cout << "Ваша Функция выглядит следующим образом:\n"; print_coeffs_fx(coeffs,n + 1); if (from_file) { cout << "[a, b] = " << "[" < cout << "epsilon = " << epsilon << endl; } while (fabs(start - end_x) > epsilon && !fx_null_average) { average = (start + end_x) / 2; if (get_fx(coeffs,n,average)*get_fx(coeffs,n,start) < 0) { end_x = average; } else if (get_fx(coeffs,n,average) == 0 ) { fx_null_average = true; } else { start = average; } } if (fx_null_average) { start = average; } cout << "Приближенное значение корня: " << start; } delete[] coeffs; return 0; } Результаты работы  Рисунок 1  Рисунок 2  Рисунок 3  Рисунок 4 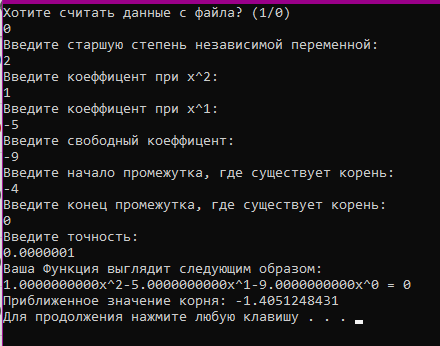 Рисунок 5 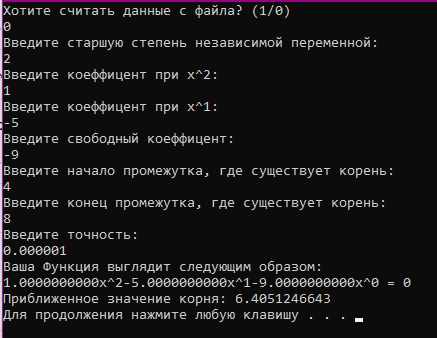 Рисунок 6 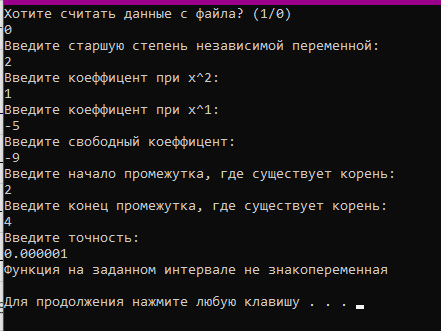 Рисунок 7 Анализ результатов работы На рисунках 1 – 4 представлена функция вида: g(x)= -0.000001750628 x^(6)-0.0000682906913 x^(5)+0.0001416568628 x^(4)+0.0201478078897 x^(3)+0.0221459728014 x^(2)-1.2207428321347 x-0.6525344491915. График этой функции: 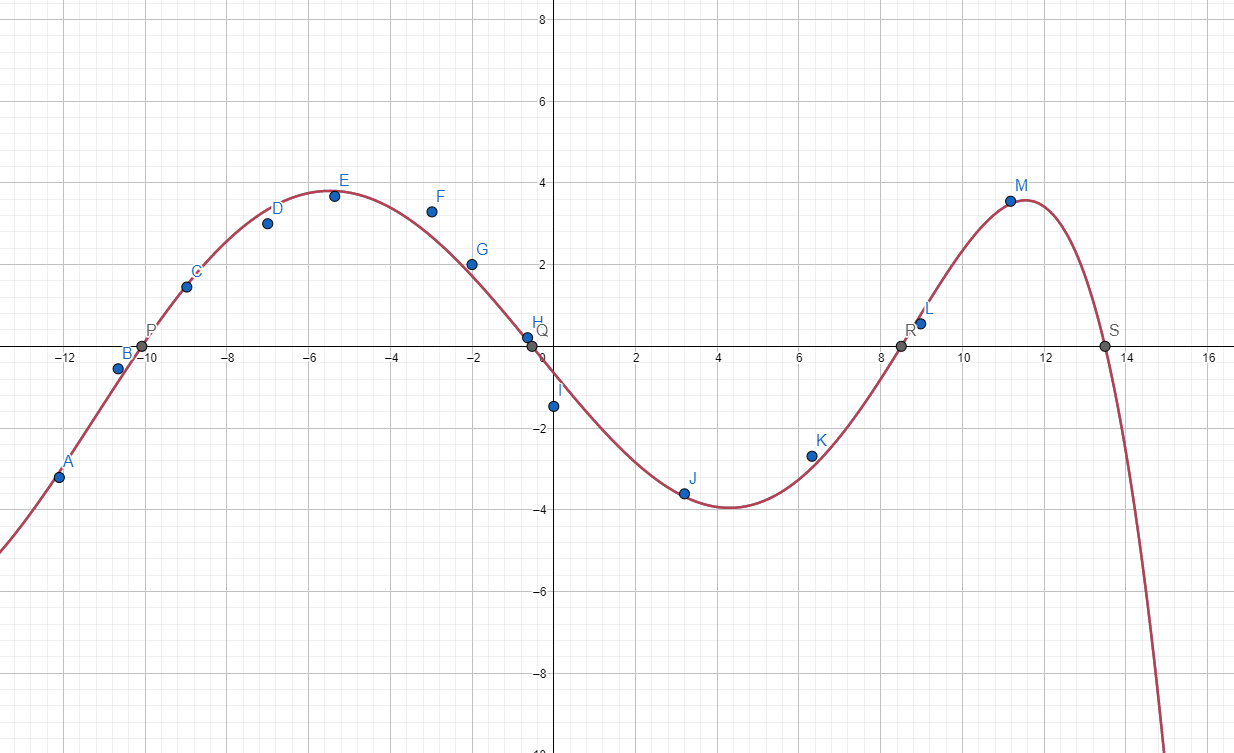 Все корни этой функции: 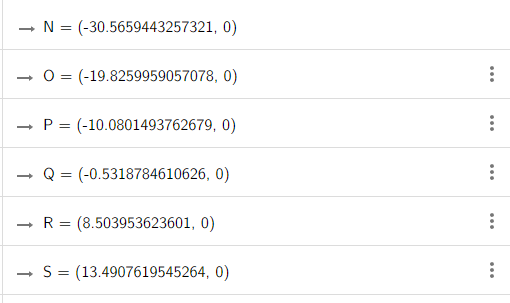 На всех заданных интервалах корни этой функции вычислены верно, удовлетворяют заданной точности. На Рисунках 5-7 была введена функция вида g(x) = x^(2)-5x-9 График этой функции: 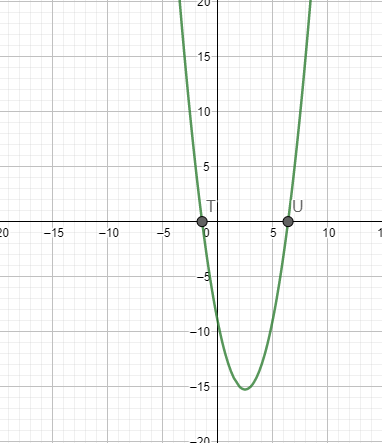 Её корни: 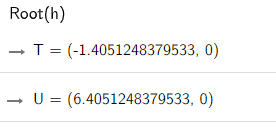 На рисунках 5-6 значения корней получены верно, с учетом заданной точности. На рисунке 7 потенциальный пользователь задал интервал, на котором функция не меняет свой знак. В ответ на это программа вывела соответствующие уведомление. |
