Примеры по высшей математике. Метод лагранджа. Матан. 1. Проверить удовлетворяет ли функция заданному уравнению
 Скачать 36.99 Kb. Скачать 36.99 Kb.
|
|
1.Проверить удовлетворяет ли функция заданному уравнению 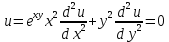 Найдем частные производные первого и второго подярка 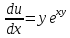 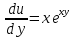 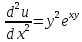 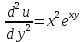 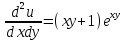 Подставим 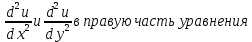 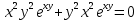 Проведем упрощения 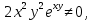 Следовательно функция не удовлетворяет заданному уравнению 2 Охарактеризовать точки безусловного экстремума и найти безусловные экстремумы следующих функций 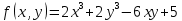 Найдем частные производные первого порядка 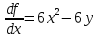 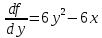 Решим систему уравнений 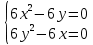 Находим критические точки функции 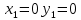 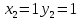 Найдем частные производные второго порядка 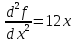 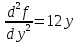 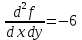 Вычисляем значения частных производных второго порядка в каждой из найденных критических точек 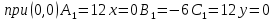 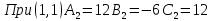 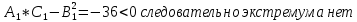 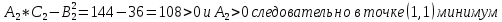 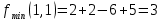 Ответ: 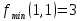 3 Охарактеризовать точки безусловного экстремума заданной функции. 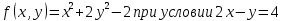 Найдем экстремум функции 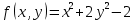 , используя функцию Лагранжа , используя функцию ЛагранжаВ качестве целевой функции, подлежащей оптимизации, в этой задаче выступает функция: 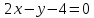 Составим вспомогательную функцию Лагранжа: 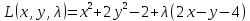 Необходимым условием экстремума функции Лагранжа является равенство нулю ее частных производных по переменным x,y и неопределенному множителю λ. Решим систему уравнений 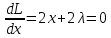 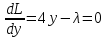 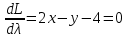 Решив данную систему, получаем стационарные точки 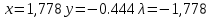 Определение типа экстремума в стационарных точках. Для определения типа экстремума необходимо вычислить матрицу Гессе для точки M(1,778; -0,444; -1.7778), либо найти значения функции в каждой из точек и выбрать экстремальное. 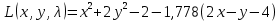 Найдем частные производные. 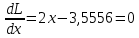 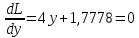 Решим систему уравнений и получим 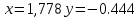 Найдем частные производные второго порядка 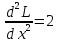 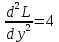 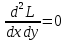 Вычислим значение этих частных производных второго порядка в стационарных точках Вычисляем значения для точки (1,778; -0,444) 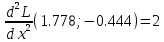 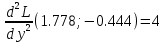 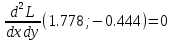 Строим матрицу Гессе: 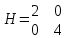 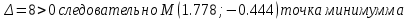 4 Методом Лагранжа найти и охарактеризовать точки локального условного экстремума 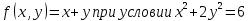 Найдем экстремум функции 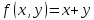 , используя функцию Лагранжа , используя функцию ЛагранжаВ качестве целевой функции, подлежащей оптимизации, в этой задаче выступает функция: 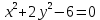 Составим вспомогательную функцию Лагранжа: 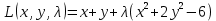 Необходимым условием экстремума функции Лагранжа является равенство нулю ее частных производных по переменным x,y и неопределенному множителю λ. Решим систему уравнений 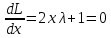 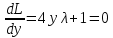 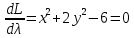 Решив данную систему, получаем стационарные точки 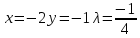 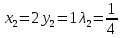 Определение типа экстремума в стационарных точках. Для определения типа экстремума необходимо вычислить матрицу Гессе для точки M1(-2;-1;-1/4); M2(2;1;1/4) либо найти значения функции в каждой из точек и выбрать экстремальное. 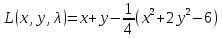 Найдем частные производные. 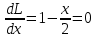 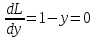 Решим систему уравнений и получим 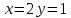 Найдем частные производные второго порядка 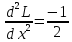 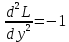 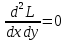 Вычислим значение этих частных производных второго порядка в стационарных точках Вычисляем значения для точки (2;1) 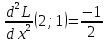 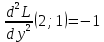 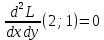 Строим матрицу Гессе: 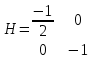 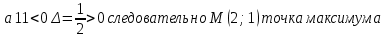 Для точки M2(2;1;1/4) Найдем частные производные. 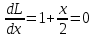 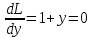 Решим систему уравнений и получим 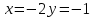 Вычислим значение этих частных производных второго порядка в стационарных точках Вычисляем значения для точки (2;1) 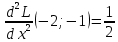 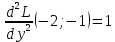 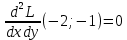 Строим матрицу Гессе: 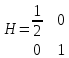 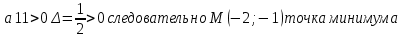 5. Найти наибольшее и наименьшее значение заданной функции в области D, ограниченной заданными графиками заданных функций 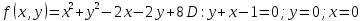 Составим вспомогательную функцию Лагранжа: 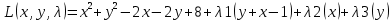 Необходимым условием экстремума функции Лагранжа является равенство нулю ее частных производных по переменным x,y и неопределенному множителю λ. Решим систему уравнений 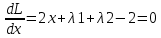 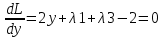 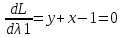 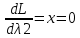 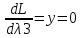 Данная система не имеет решений, следовательно точек минимума и максимума в указанной области нет. 6. Найти параметры линейной зависимости по данным таблицы методом наименьших квадратов и записать полученную линейную функцию
1.Найдем квадраты х, у и их произведение 2.Составим систему уравнений 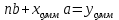 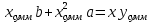 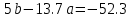 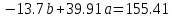 Из первого уравнения выражаем a и подставим во второе уравнение Получаем 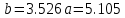 Получаем линейное уравнение 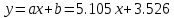 3.Найдем Y`, подставив в 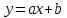 наши значения Х наши значения Х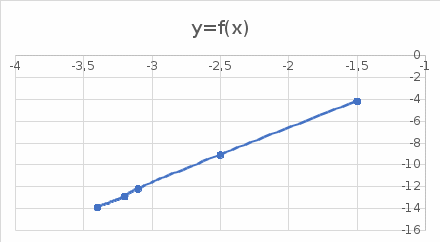 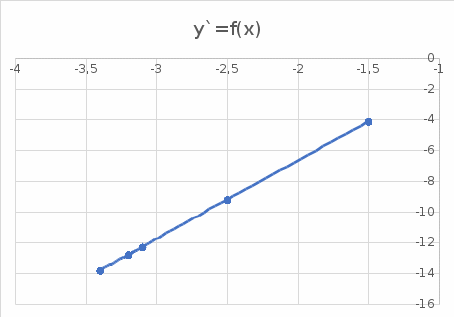 |
