Отчет по УИР. Пермский национальный исследовательский политехнический университет Аэрокосмический факультет кафедра Авиационные двигатели
 Скачать 2.55 Mb. Скачать 2.55 Mb.
|
|
Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Пермский национальный исследовательский политехнический университет» Аэрокосмический факультет кафедра «Авиационные двигатели» Специальность 24.05.02 (160700) «Проектирование авиационных и ракетных двигателей». О Т Ч Е Т по практическим занятиям по дисциплине ИНЖЕНЕРНО-ВЫЧИСЛИТЕЛЬНЫЕ ТЕХНОЛОГИИ Выполнили студенты гр.АД-19-1С ___________________________________________ (подпись) Проверил: _____ст. преподаватель кафедры КОНЕВ И.П.________ (должность, Ф.И.О. преподавателя) ___________ _________________________ (оценка) (подпись) _____________ (дата) Пермь 2021 Лабораторная работа №1 Простейшие вычисления ЗАДАНИЕ 1: а) вычислить значение функции y =f(x) в точке х0 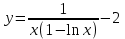 (вар 4) (вар 4)х0 =4,21 хn =7,6 >> x=4.21; >> y=1/(x*(1-log(x)))-2 y = -2.5430 б) простроить график функции y =f(x) используя встроенную функцию MatLab poly(x,y) на интервале от х0 до хn , шаг аргумента x определить самостоятельно >> x=4.21:0.01:7.6; >> y=1./(x.*(1-log(x)))-2 y = -2.5430 -2.5388 -2.5346 -2.5305 -2.5265 -2.5225 -2.5186 >> plot(x,y) 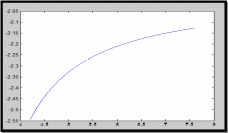 Рис.2 График функции 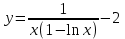 Вывод: MatLAB позволяет вычислять значение функции y =f(x) в точке х0 и строить графики с помощью встроенной функции poly(x,y). Лабораторная работа №2 Символьные вычисления в MatLab ЗАДАНИЕ 1: Решить алгебраические уравнения, используя команду solve:  >> [x]=solve('1/(x+3)+(x+8)/(2*x^2-18)=1/(3-x)-1') x =105^(1/2)/4 - 5/4 - 105^(1/2)/4 - 5/4 ЗАДАНИЕ 2: Решить систему алгебраических уравнений, используя команду solve. 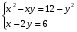 >> [ x, y ] = solve ('x^2-x*y=12-y^2', 'x-2*y=6') x = 2, -2 y = -2, -4 ЗАДАНИЕ 3: Упростить выражения, используя команду simplify:  >> syms c >> p=(c/(c-2)-c/(c+2)-(c^2+4)/(4-c^2))*(2-c)^2/(2*c+c) p = ((c - 2)^2*((c^2 + 4)/(c^2 - 4) + c/(c - 2) - c/(c + 2)))/(3*c) >> simplify(p) ans = (c^2 - 4)/(3*c) ЗАДАНИЕ 4: Вычислить сумму ряда, используя команду symsum. 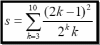 >> syms k x >> s=symsum((2*k)-1)^2/2^k/k, 3,10) >> s=symsum((2*k-1)^2/2^k/k, 3,10) s = 195155/64512 ЗАДАНИЕ 5: Вычислить производную функции по х, используя команду diff. 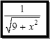 >> syms x >> y=1/sqrt(9+x^2) y =1/(x^2 + 9)^(1/2) >> diff(y) ans = -x/(x^2 + 9)^(3/2) ЗАДАНИЕ 6: Используя функцию int, подготовить и организовать вычисление определенного интеграла: 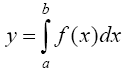 Подынтегральная функция f(x) определена и непрерывна на интервале a <= x <= b. 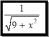 >> syms x a b >> int(1/sqrt(9+x^2),0,2) ans = log(13^(1/2)/3 + 2/3) Вывод: MatLAB позволяет вычислять производные, интегралы, находить сумму ряда, упрощать выражения и т.д. с помощью специальных функций. Лабораторная работа №3 Высокоуровневая графика в MatLAB Цели работы: 1. Знакомство с основными возможностями высокоуровневой (high-level) графики MATLAB для отображения функций двух и трёх переменных, визуализации векторных и матричных данных и векторных полей. Для выполнения данной лабораторной работы необходимо уметь работать с массивами — векторами и матрицами, понимать выполнение поэлементных операций с массивами. Задание 1. Построить графики функций. Использовать функцию plot. Нужно самостоятельно задать шаг и диапазон изменения аргумента y 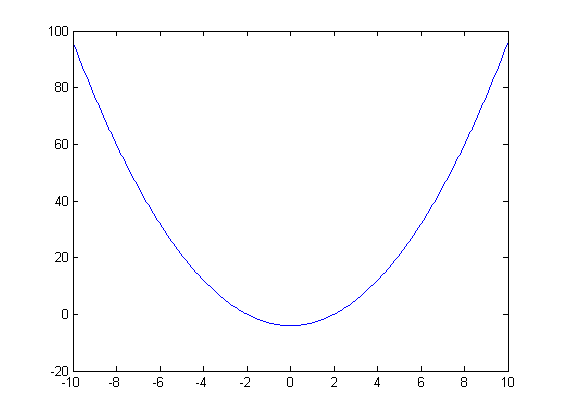 = x^ 2 – 4 ; = x^ 2 – 4 ;y = x ^4 - 4x ^2 ; y = sin (x) + log (x). 1)x= 3; >> y= x^2 -4 y = 5 >> x = -10 : 0.05 :10 ; >> y= x.^2 -4 y = plot(x,y) Рисунок 1: График функции y = x^ 2-4 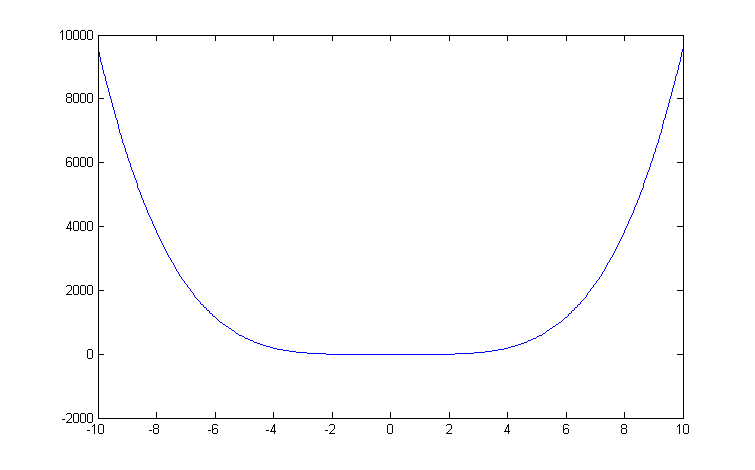 2) x= 5; >> y= x^4 - 4*x^2 y = 525 >> x = -10 : 0.05 : 10 ; >> y= x.^4- 4.*x.^2 y =plot(x,y) Рисунок 2: График функции y= x^4- 4*x^2 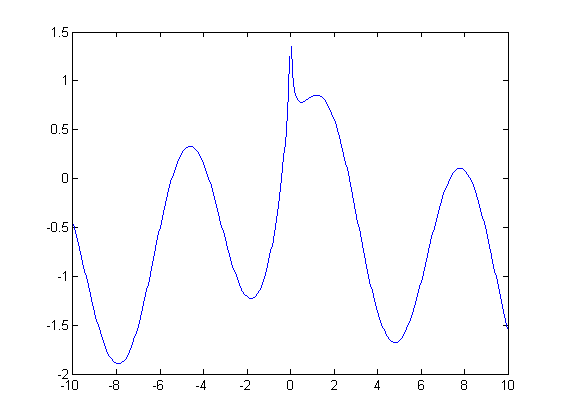 3) x = 5; >> y = sin(x)-log10(x) y = -1.657894278999157 >> x= -10 :0.05 : 10; >> y= sin(x)-log10(x) y = plot(x,y) Рисунок 3: График функции y = sin(x)-log10(x) Задание 2. Построить кривые, заданные параметрически. Использовать функцию plot. Уравнение кривой: x (t) = t – sin (t) , y (t) = 1- cos (t) – постройте эту кривую при t, изменяющимся в диапазоне [-π;π]. – постройте эту кривую при t, изменяющимся в диапазоне [0;2π]. a) t = -pi:0.1:pi; >> x = 1-sin(t); >> y = 1- cos(t); plot (x,y), grid, set(gcf,'color', 'white') 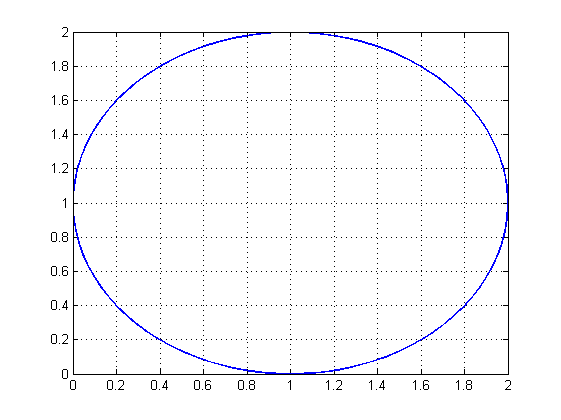 Рисунок 4: График функции x (t) = t – sin (t) , y (t) = 1- cos (t) [-π;π]  b) Рисунок 5: График функции x (t) = t – sin (t) , y (t) = 1- cos (t) [0;2π] Задание 3. Построить кривые, заданные в полярной системе координат в диапазоне [0; 2π]. Использовать функцию polar. – кривая задана уравнением r = 1 + sin (t). – кривая задана уравнением r = 1 + cos (2t). t = 0:0.1:2*pi; r = 1+sin(t); polar(r,t), grid, set(gcf,'color', 'white') 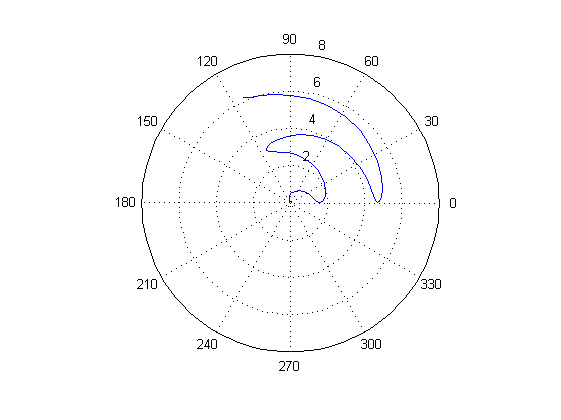 Рисунок 6: График функции r = 1 + sin (t) [0;2π] t 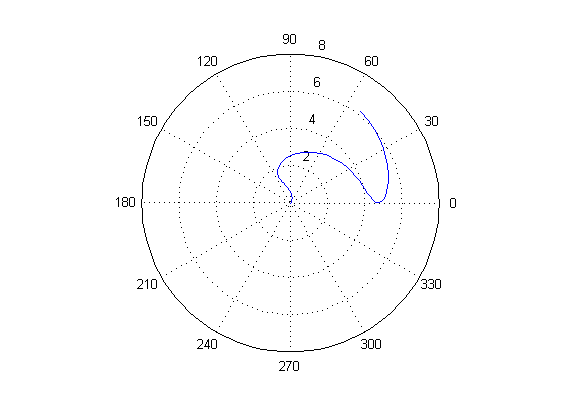 = 0:0.1:2*pi; = 0:0.1:2*pi; r = 1+cos(2*t); polar(r,t), grid, set(gcf,'color', 'white') Рисунок 7: График функции r = 1 + cos (2t) [0;2π] Задание 4. Построить графики трёхмерных поверхностей. Использовать функции meshgrid, plot . – график трёхмерной поверхности, описываемый функцией 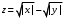 – график трёхмерной поверхности, описываемый функцией z = y2 - x2. 1) [X, Y] = meshgrid(-1:0.05:1, 0:0.05:1); Z = sqrt(abs(X))-sqrt(abs(Y)); m 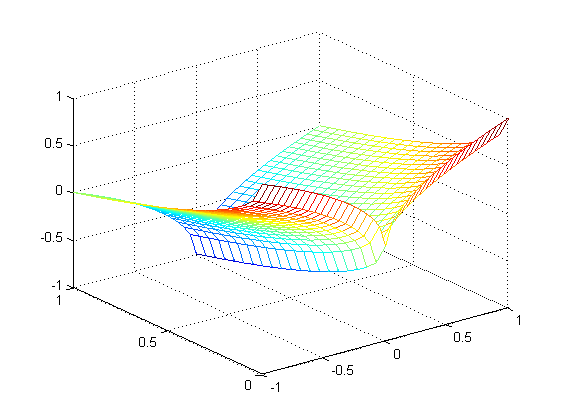 esh(X, Y, Z) esh(X, Y, Z)Рисунок 8: График трёхмерной поверхности 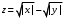 2) [X, Y] = meshgrid(-1:0.05:1, 0:0.05:1); Z = X.^2-Y.^2; mesh(X, Y, Z) 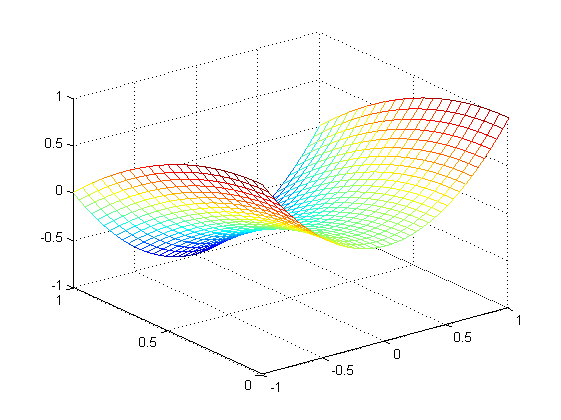 Рисунок 9: График трёхмерной поверхности z = y2 - x2 Задание 5. Построить в декартовой системе координат график вектора с комплексными элементами у = sin x + i *cos x в диапазоне [0; 2 π], используя функцию plot. x= 0: 0.05 : 2*pi; >> y = sin(x) + i *cos( x ) y = plot(x,y) 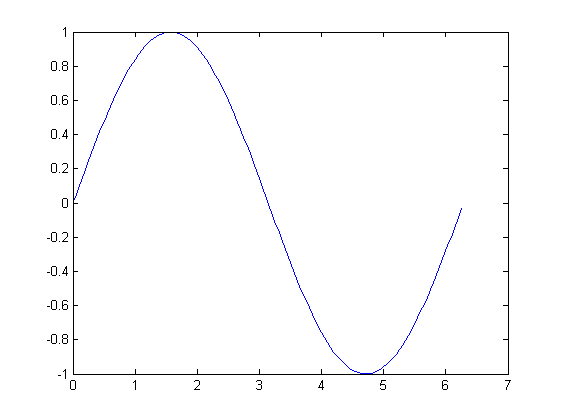 Рисунок 10: График функции у = sin x + i *cos x [0;2π] Рисунок 10: График функции у = sin x + i *cos x [0;2π]Задание 8. Постройте два графика в рамках одних осей координат: 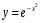 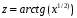 для для 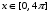 Сделайте надписи на осях, заголовок для графика, пояснительную надпись на рисунке задайте тип линий и цвет. x=0:0.05:4*pi; >> z = atan(x.^(1/2)); >> y=exp(-x.^2); z = atan(x.^(1/2)); >> plot(x,y,x,z),grid >> title('Функции y = y=exp(-x^2) и z = atan(x^(1/2)) '); >> xlabel('ось X'); ylabel('ось Y'); 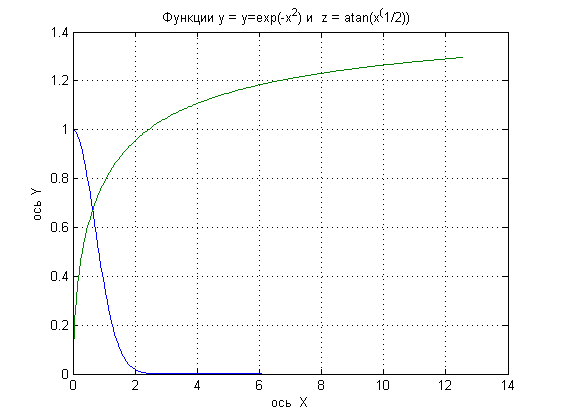 Рисунок 11: Графики функций y=exp(-x.^2); z = atan(x.^(1/2)) в одних осях Задание 9. Построить графики функций y(x) и z(x) в разных подобластях одного графического окна. Интервалы изменения для х определите самостоятельно. x1=0:0.05:2*pi; >> z = atan(x1.^(1/2)); >> x2=0:0.05:4*pi; >> y=exp(-x2.^2); >> plot(x1,z,x2,y) 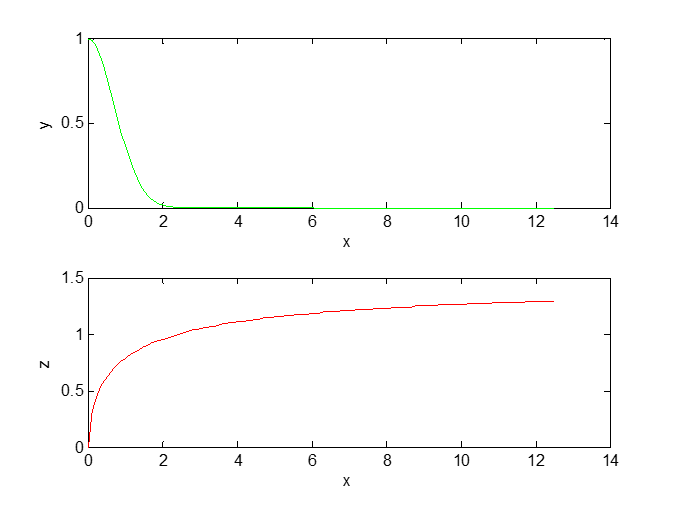 Рисунок 12: Графики функций y=exp(-x.^2); z = atan(x.^(1/2)) в разных подобластях Задание 10. Постройте поверхность с использованием функции mesh 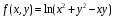 , где , где 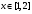 >> [x,y] = meshgrid(1:0.1:2, -5:0.1:5) >> z = log(x.^2+y.^2-x.*y) >> mesh(x, y, z); xlabel('x'); ylabel('y'); zlabel('z') 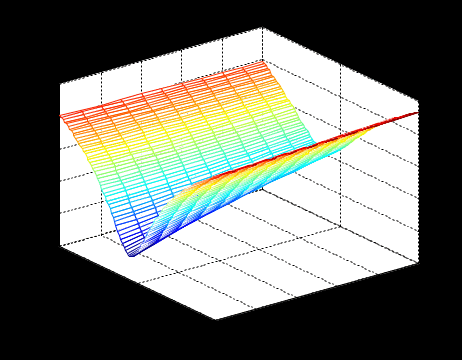 Рисунок 13: График трёхмерной поверхности z = log(x.^2+y.^2-x.*y) Вывод: В MatLAB можно строить различные графики функций, как в декартовых, так и в полярных координатах, строить трехмерные поверхности, строить несколько графиков на одном поле и т. п. Все это реализуется с помощью специальных встроенных функций. Лабораторная работа № 4. Решение типовых задач алгебры и анализа Создание процедур (файлов-функций) в среде MatLAB Цель работы: Целью лабораторной работы является изучение простых приемов языка программирования среды MatLAB. Основной задачей ставится изучение типовых конструкций языка, таких как функции, условия и циклы. Задание №1 Создайте m-файл, вычисляющий значения функции f(x)на отрезке [a; b] с шагом h (Таблица 2.1). Постройте график этой функции с помощью процедуры fplotв границах, заданных в задании. Вычислите интеграл от функции в тех же пределах, используя встроенные функции. Найдите экстремумы и ближайший корень (нуль) функции. 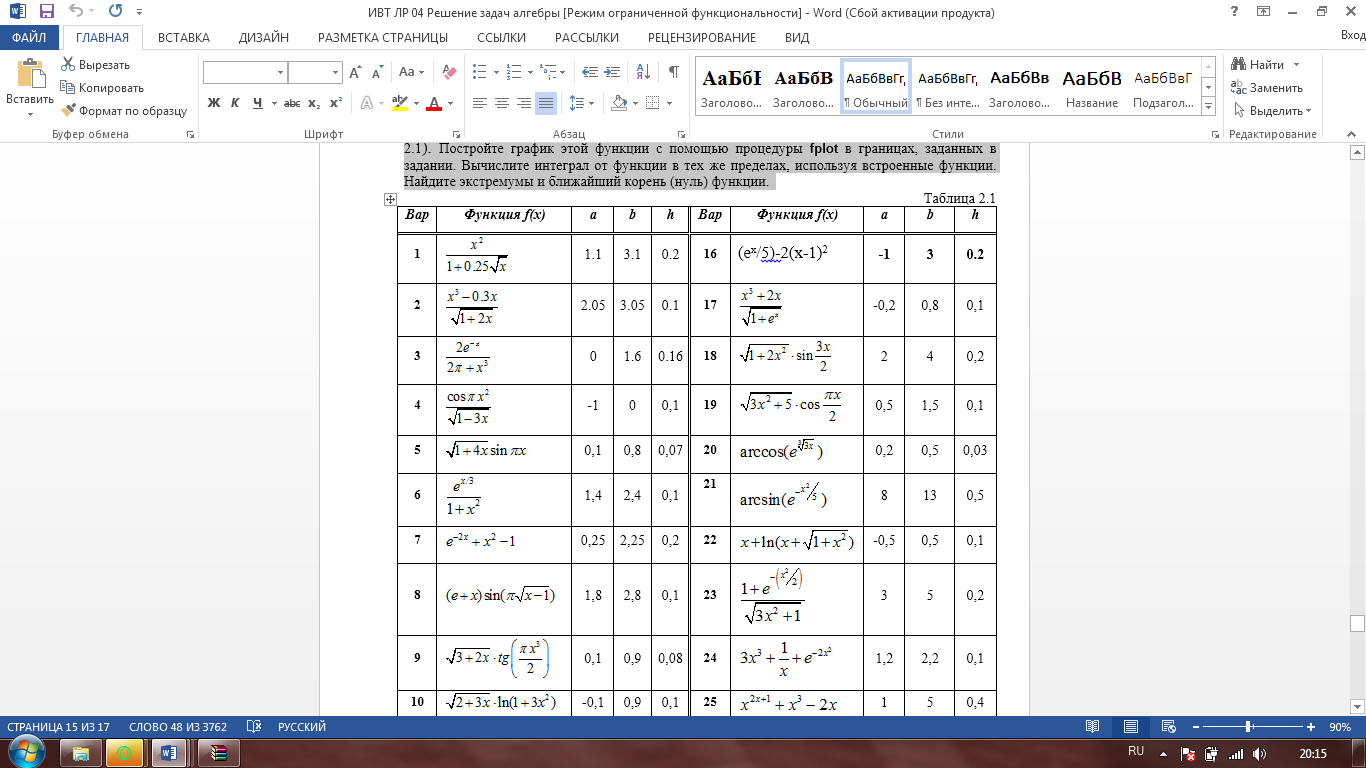 function [ y ] = func( x ) %Вычисляет значение функции %y=cos(pi*x^2)/sqrt(1-3*x) y=cos(pi.*x.^2)./sqrt(1-3*x); end fplot(‘func’, [-1,0], 0.1, 1), grid, title(‘График функции “ y=cos(pi*x^2)/sqrt(1-3*x) “’); >> x=-1:0.1:0; >> y=func(x); >> int=trapz(x,y) int = 0.3257 >> x=-1:0.1:0; >> y=cos(pi.*x.^2)./sqrt(1-3*x); >> plot(x,y,'-k'),grid >> y=func(x); >> [xmin,ymin]=fminsearch(@func,-1) xmin = -0.9903 ymin = -0.5009 function [ y ] = func( x ) %Вычисляет значение функции %y=cos(pi*x^2)/sqrt(1-3*x) y=-(cos(pi.*x.^2)./sqrt(1-3*x)); end >> x=-1:0.1:0; >> y=funca(x); >> plot(x,y,'-k'),grid >> [xmax,ymax]=fminsearch(@funca,-1) xmax = -1.4105 ymax = -0.4370 >> x=-1:0.1:0; >> y=cos(pi.*x.^2)./sqrt(1-3*x); >> y=func(x); >> plot(x,y), grid >> x1=fzero(@func,-0.8) x1 =-0.7071 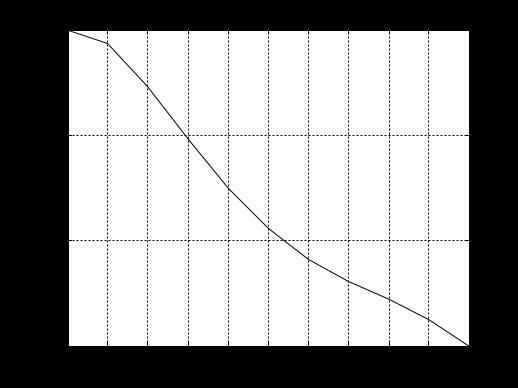 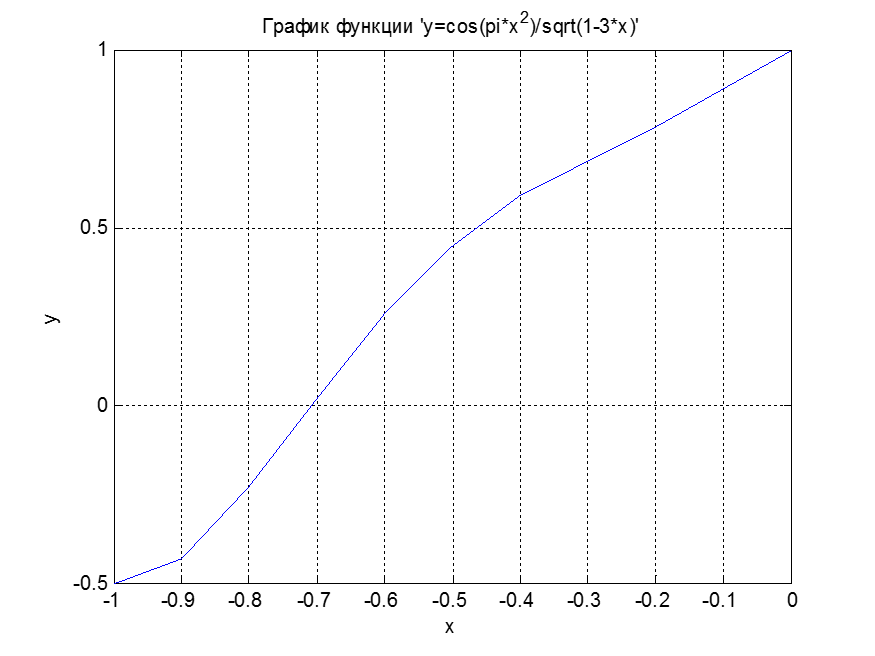 Рисунок 1: График функции y=cos(pi.*x.^2)./sqrt(1-3*x) Рисунок 1: График функции y=cos(pi.*x.^2)./sqrt(1-3*x)Рисунок 2: График функции y=cos(pi.*x.^2)./sqrt(1-3*x) Задание №2 Найдите локальные экстремумы функции двух переменных, приняв за начальную, точку с заданными координатами x0, y0 (таблица 2.1). Предварительно создайте соответствующую файл-функцию. >> [z,fval] = fminsearch(@(x) (exp(x(1)+x(2))+4.*x(1).^2-3.*x(1)-3.*x(2)), [0.5,1.5]) z = 0.0000 1.0986 fval = -0.2958 >> [x,y]=meshgrid(-2:0.2:2,-2:0.2:2); >> z= exp(x+y)+4.*x.^2-3.*x-3.*y; >> surf(x,y,z); >> [x,fval] = fminunc(@(x) (exp(x(1)+x(2))+4.*x(1).^2-3.*x(1)-3.*x(2)), [0.5,1.5]) Warning: Gradient must be provided for trust-region algorithm; using line-search algorithm instead. > In fminunc at 380 Local minimum found. Optimization completed because the size of the gradient is less than the default value of the function tolerance. x = 0.0000 1.0986 fval =-0.2958 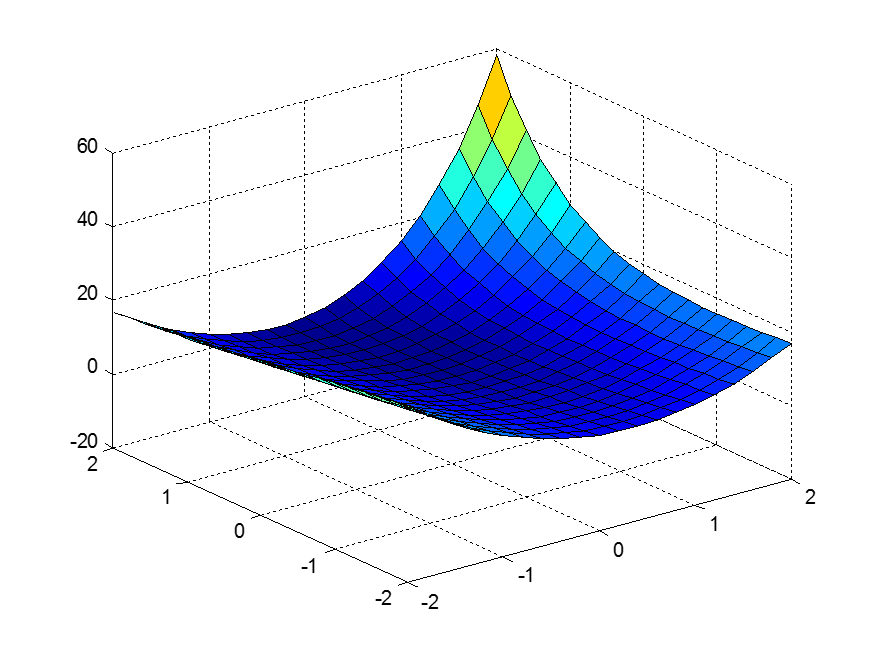 Рисунок 3: Поверхность z= exp(x+y)+4.*x.^2-3.*x-3.*y Задание №3 Рассчитать аэродинамический нагрев тела в полете со скоростью V, в зависимости от высоты полета H для условий международной стандартной атмосферы (МСА). Значение высоты H принять от 0 до 25000м с шагом 1000м. Зависимость температуры атмосферы TH[K]от высоты Н[м] определяется по формуле: TH= T0 - β·Н где β - коэффициент снижения температуры β = 6,5·10-3 [K/м]; T0 – температура атмосферы на высоте Н = 0, T0=288,2[K] Начиная с высоты 11000м (тропосфера) до высоты 25000м (стратосфера) температура окружающей среды остается постоянной. Аэродинамический нагрев ΔT*[K] рассчитывается по формуле: 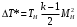 где МН – число Маха 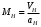 ; аН – местная скорость звука [м/с], определяется по формуле ; аН – местная скорость звука [м/с], определяется по формуле 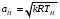 . .Показатель адиабаты для воздуха k =1,4. Удельная газовая постоянная R = 287,13[Дж/кг·К] Варианты исходных данных (скорость полета VH)
1. Вывести рассчитанные данные зависимостей TH (Н) и ΔT*(Н) в виде таблиц. Для чего после расчета сохранить их в текстовый файл. 2. Построить графики этих зависимостей. Th(H):
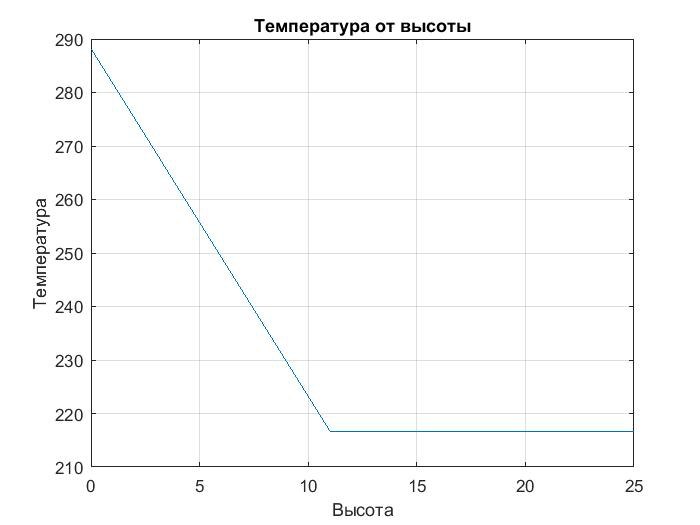 Рисунок 4: График зависимости температуры от высоты а(h):
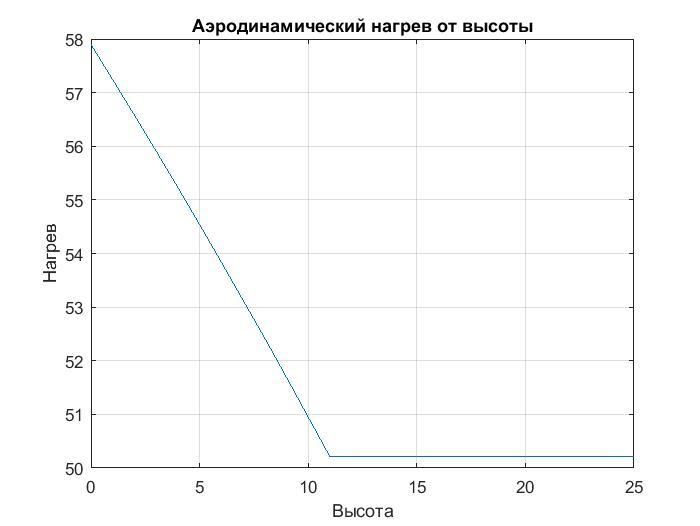 Рисунок 5: График зависимости аэродинамического нагрева от высоты Вывод: MatLAB позволяет исследовать математические функциональные зависимости на максимумы и минимумы, экстремумы и находить точки пересечения функции с осями координат, а также решать практические задачи. Лабораторная работа № 5. Методы обработки экспериментальных данных Основы работы в Curve Fitting Toolbox Цель: 1) научиться работать с Curve Fitting Toolbox; 2) определить вид заданной функции. Curve Fitting Toolbox позволяет: 1. Работать с данными, заданными при помощи векторов в рабочей среде MATLAB, и, при необходимости, снабжать данные весами, так же задавая вектор их значений. 2. Графически отображать исследуемые данные. 3. Осуществлять предварительную обработку данных, исключая часть данных по некоторому правилу, по точкам в таблице, или при помощи мыши на графике, или наоборот оставляя часть данных для последующей обработки. 4. Сглаживать и фильтровать данные различными способами. 5. Приближать данные при помощи параметрических моделей, в которых искомые параметры могут входить как линейно, так и нелинейно. Модели выбираются из библиотеки моделей, или задаются пользователем. Целевая функция ошибки и методы, применяемые для ее минимизации, так же могут быть различными. Допускается задание ограничений на искомые значения параметров. Кроме параметрических моделей, возможна интерполяция данных сплайнами и приближение сглаживающими сплайнами. 6. Отображать построенные приближения графически, форматировать графики и сохранять результаты в отдельных графических окнах. 7. Вычислять различные критерии пригодности полученного приближения. 8. Производить ряд операций с полученными приближениями (вычислять в заданных точках, дифференцировать интегрировать, проводить экстраполяцию), графически отображать результат. П 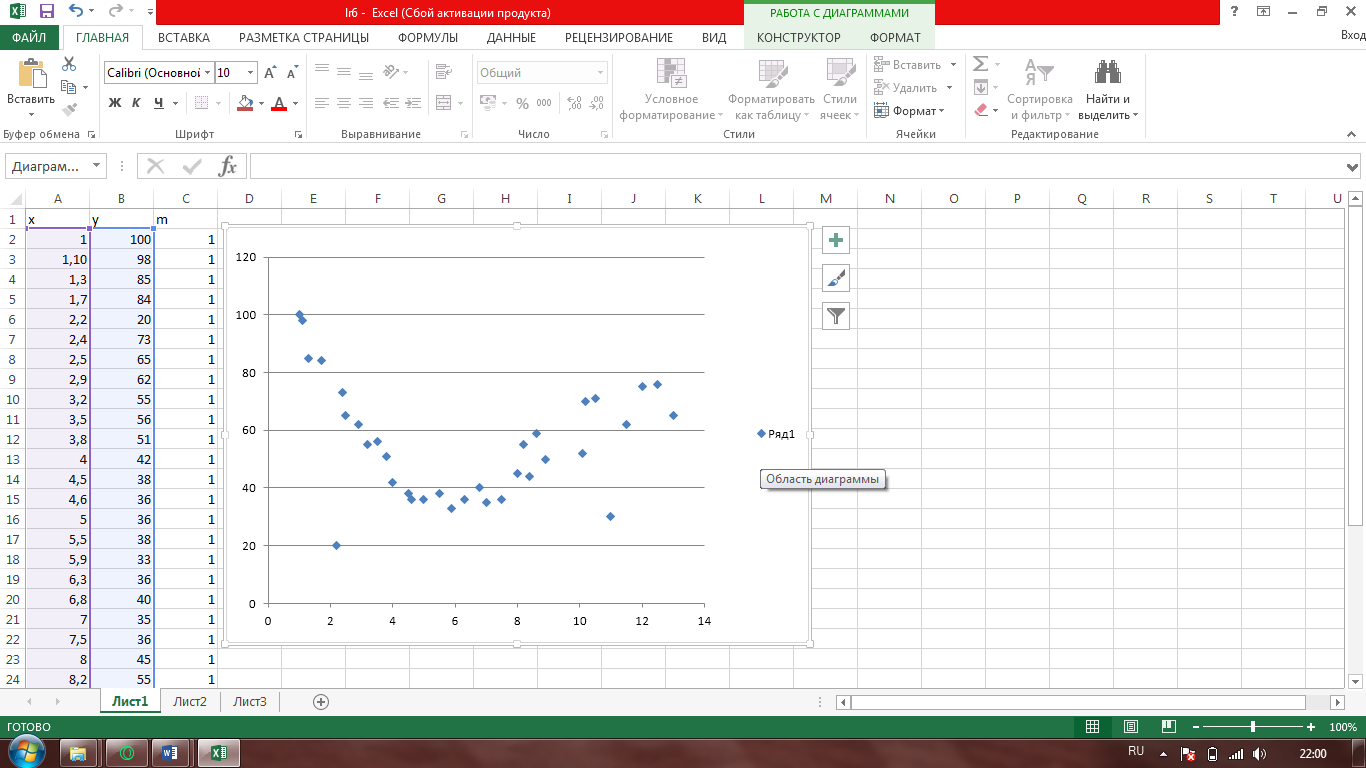 риблизительно были определены точки по графику неизвестной функции, построена точечная диаграмма в программе MS Excel: риблизительно были определены точки по графику неизвестной функции, построена точечная диаграмма в программе MS Excel:Рис. 1. Примерный вид графика Импортируем данные о значениях координатах и массах точек. Построенной точечной диаграмме сопоставляем предложенные программой виды различных функций. Находим функцию, которая имеет минимальные ошибки. 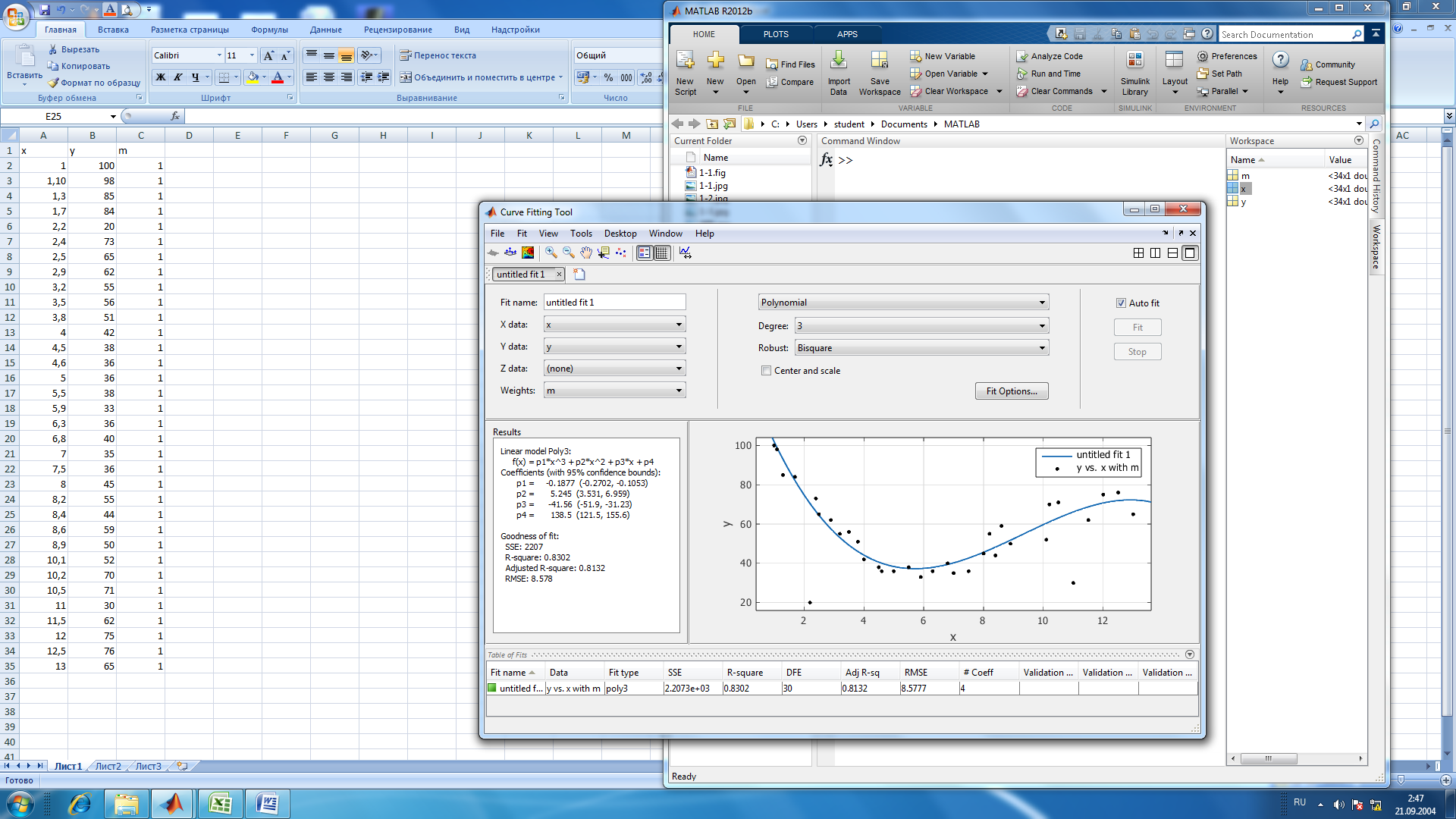 Рис.2. Результаты приближения данных полиномом третьей степени Linear model Poly3: f(x) = p1*x^3 + p2*x^2 + p3*x + p4 Coefficients (with 95% confidence bounds): p1 = -0.1877 (-0.2702, -0.1053) p2 = 5.245 (3.531, 6.959) p3 = -41.56 (-51.9, -31.23) p4 = 138.5 (121.5, 155.6) Goodness of fit: SSE: 2207 R-square: 0.8302 Adjusted R-square: 0.8132 RMSE: 8.578 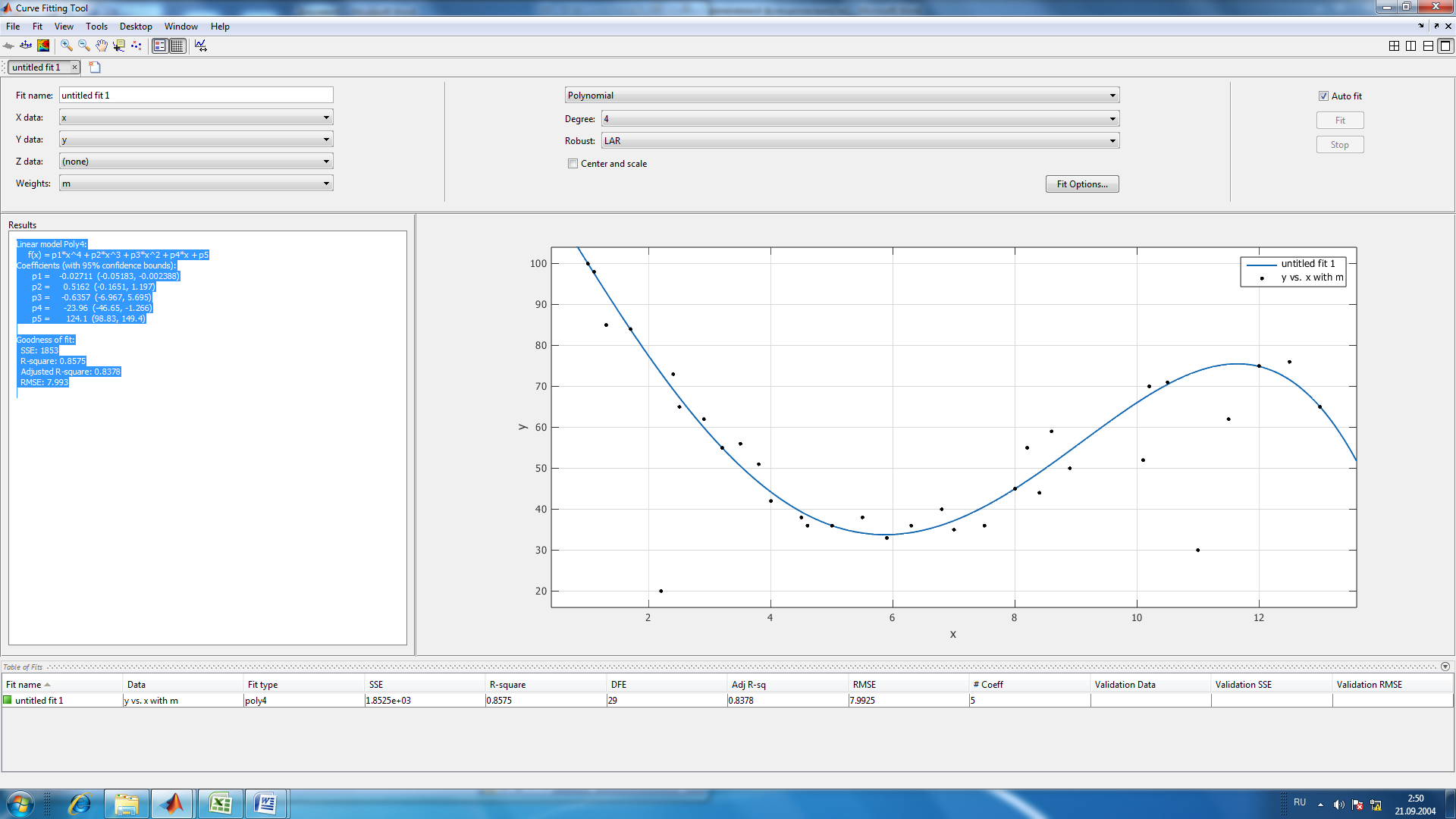 Рис.3. Результаты приближения данных полиномом четвертой степени Linear model Poly4: f(x) = p1*x^4 + p2*x^3 + p3*x^2 + p4*x + p5 Coefficients (with 95% confidence bounds): p1 = -0.02711 (-0.05183, -0.002388) p2 = 0.5162 (-0.1651, 1.197) p3 = -0.6357 (-6.967, 5.695) p4 = -23.96 (-46.65, -1.266) p5 = 124.1 (98.83, 149.4) Goodness of fit: SSE: 1853 R-square: 0.8575 Adjusted R-square: 0.8378 RMSE: 7.993 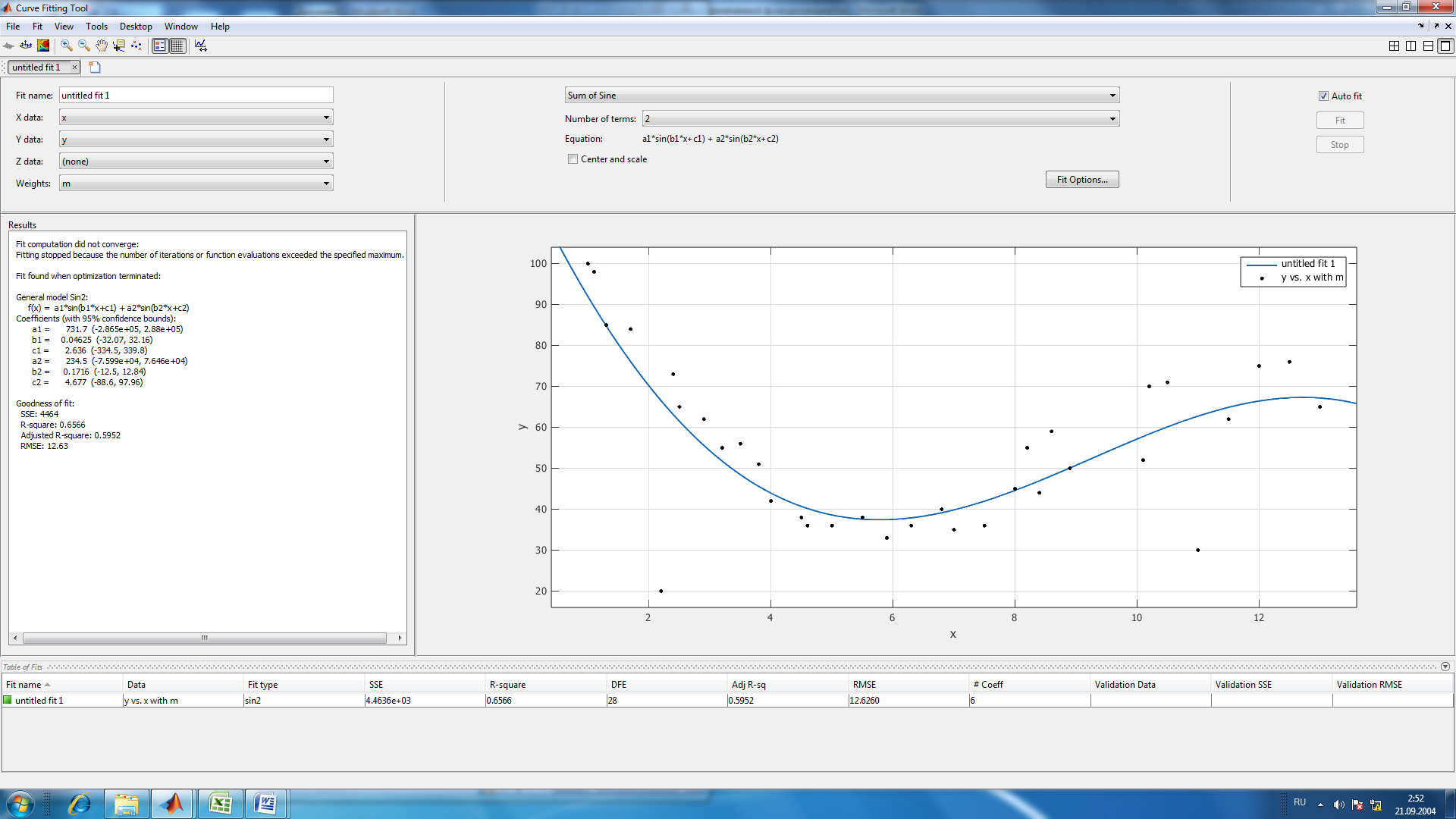 Рис.4. Результаты приближения данных функцией суммы синусов Fit computation did not converge: Fitting stopped because the number of iterations or function evaluations exceeded the specified maximum. Fit found when optimization terminated: General model Sin2: f(x) = a1*sin(b1*x+c1) + a2*sin(b2*x+c2) Coefficients (with 95% confidence bounds): a1 = 731.7 (-2.865e+05, 2.88e+05) b1 = 0.04625 (-32.07, 32.16) c1 = 2.636 (-334.5, 339.8) a2 = 234.5 (-7.599e+04, 7.646e+04) b2 = 0.1716 (-12.5, 12.84) c2 = 4.677 (-88.6, 97.96) Goodness of fit: SSE: 4464 R-square: 0.6566 Adjusted R-square: 0.5952 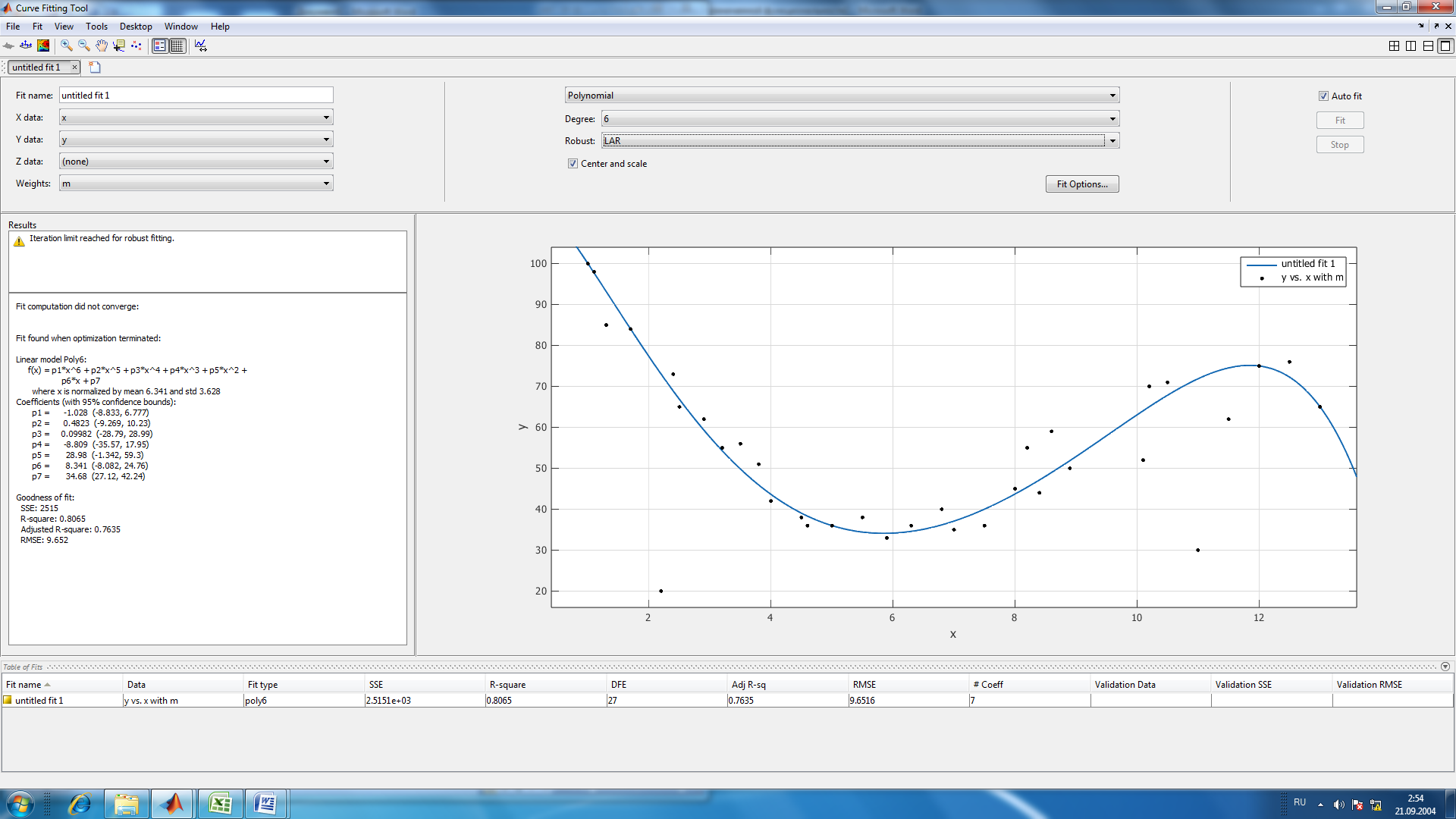 RMSE: 12.63 RMSE: 12.63Рис.5. Результаты приближения данных полиномом шестой степени Fit computation did not converge: Fit found when optimization terminated: Linear model Poly6: f(x) = p1*x^6 + p2*x^5 + p3*x^4 + p4*x^3 + p5*x^2 + p6*x + p7 where x is normalized by mean 6.341 and std 3.628 Coefficients (with 95% confidence bounds): p1 = -1.028 (-8.833, 6.777) p2 = 0.4823 (-9.269, 10.23) p3 = 0.09982 (-28.79, 28.99) p4 = -8.809 (-35.57, 17.95) p5 = 28.98 (-1.342, 59.3) p6 = 8.341 (-8.082, 24.76) p7 = 34.68 (27.12, 42.24) Goodness of fit: SSE: 2515 R-square: 0.8065 Adjusted R-square: 0.7635 RMSE: 9.652 Вывод: 1) В Matlab с помощью средств Curve, Fitting и Toolbox можно определять вид любой неизвестной функции, коэффициенты уравнения, которыми она задана, рассчитать погрешность, с которой построена эта функция относительно приближенных значений. 2) Минимальные значения ошибок достигаются при приближении полиномом четвертой степени. Значение SSE должно стремиться к нулю, но, в связи с большими значениями функции по Х и по У, SSE увеличился. Контрольное задание Разработать алгоритм в виде блок-схемы. Оформить программы поиска корней уравнений из табл. 1.2. по вариантам методом сканирования и уточнения значения корней методом хорд и методом половинного деления. Сравнить количество итераций при решении уравнений методами половинного деления и хорд с заданной точностью вычислений. Код: xn=1; xk=4; % c=0; % x0=0; step_x=0.01; x=xn:step_x:xk; y=(x-5).^2.*log(x)-1.2; plot(x,y),grid; disp(""); a=input("a= "); b=input("b= "); epsilon=0.0001; %input("погрешность e1= "); for i=1:15 epsilon=0.1^i; n=0; while((b-a)>epsilon) c=(a+b)/2; ya=kontrF(a); yb=kontrF(b); yc=kontrF(c); if(ya*yc<0) b=c; else a=c; end n=n+1; end disp(fprintf('Корень, вычисленный методом половинных отрезков = %.15f за %d итераций',c,n)); input("Правая граница a= "); input("Левая граница b= "); n2=0; while((b-a)>epsilon) ya=kontrF(a); yb=kontrF(b); c=(a*abs(yb)+abs(ya)*b)/(abs(yb)+abs(ya)); yc=kontrF(c); if(ya*yc<0) b=c; else a=c; end n2=n2+1; end end disp(fprintf('Корень, вычисленный методом хорд = %.15f за %d итераций',c,n2)); Функция kontrF: function [y] = code(x) y=(x-5)^2*log(x)-1.2; end 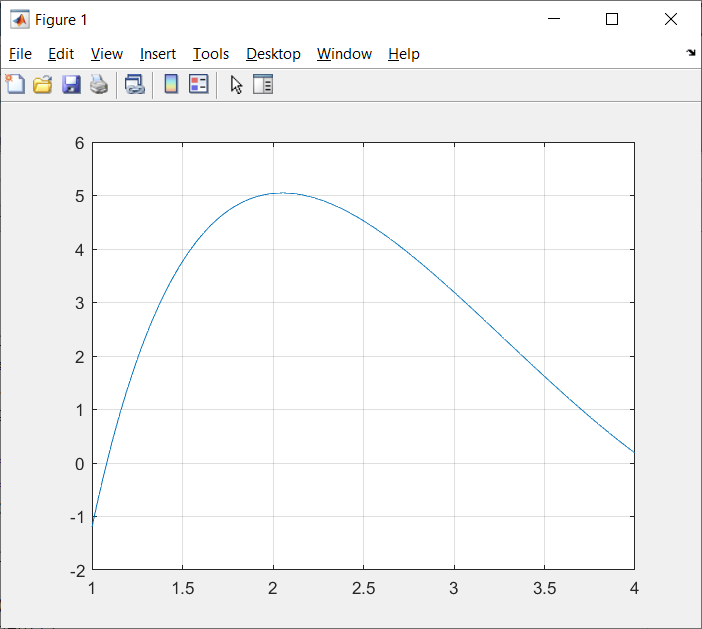 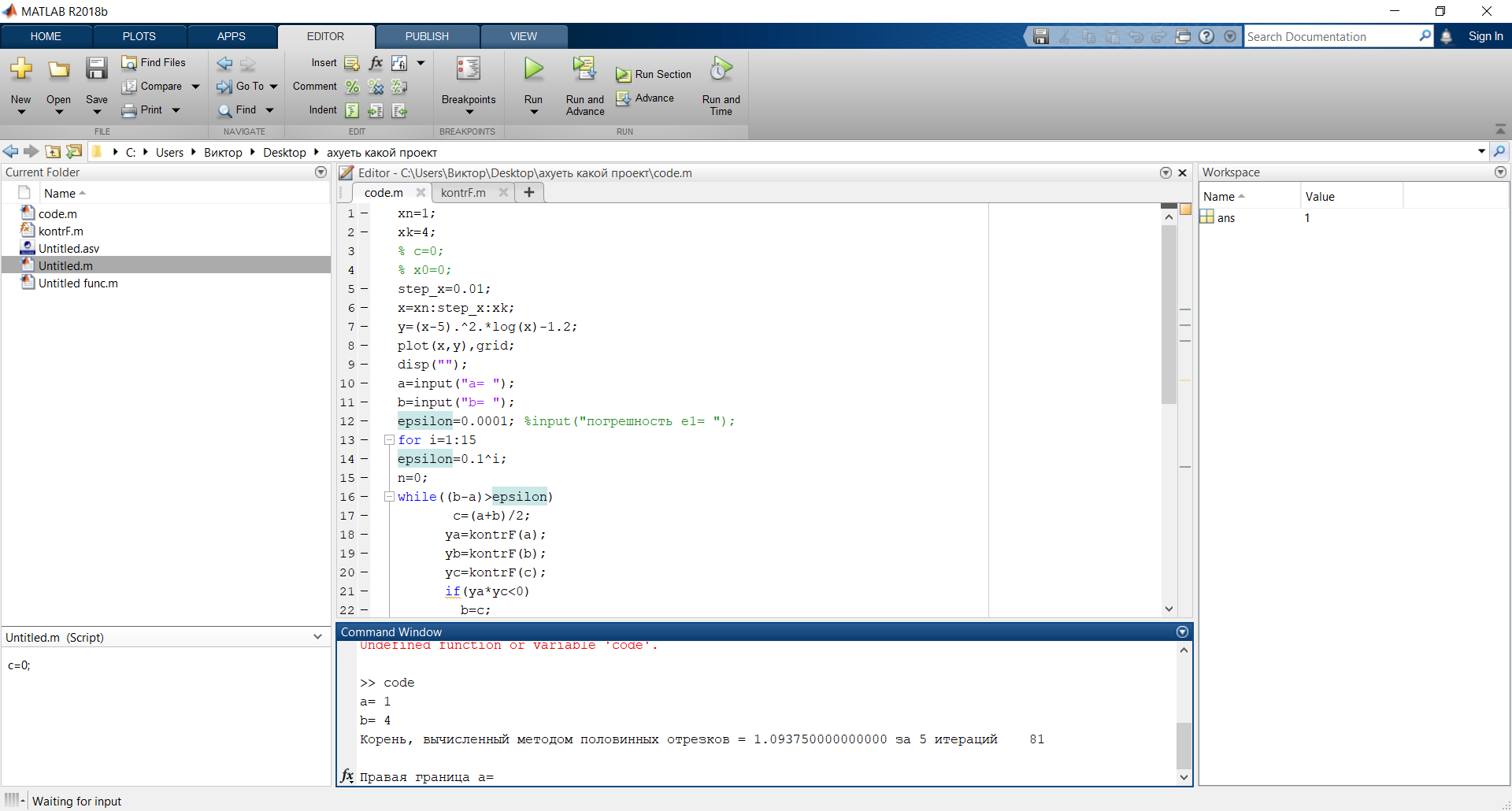 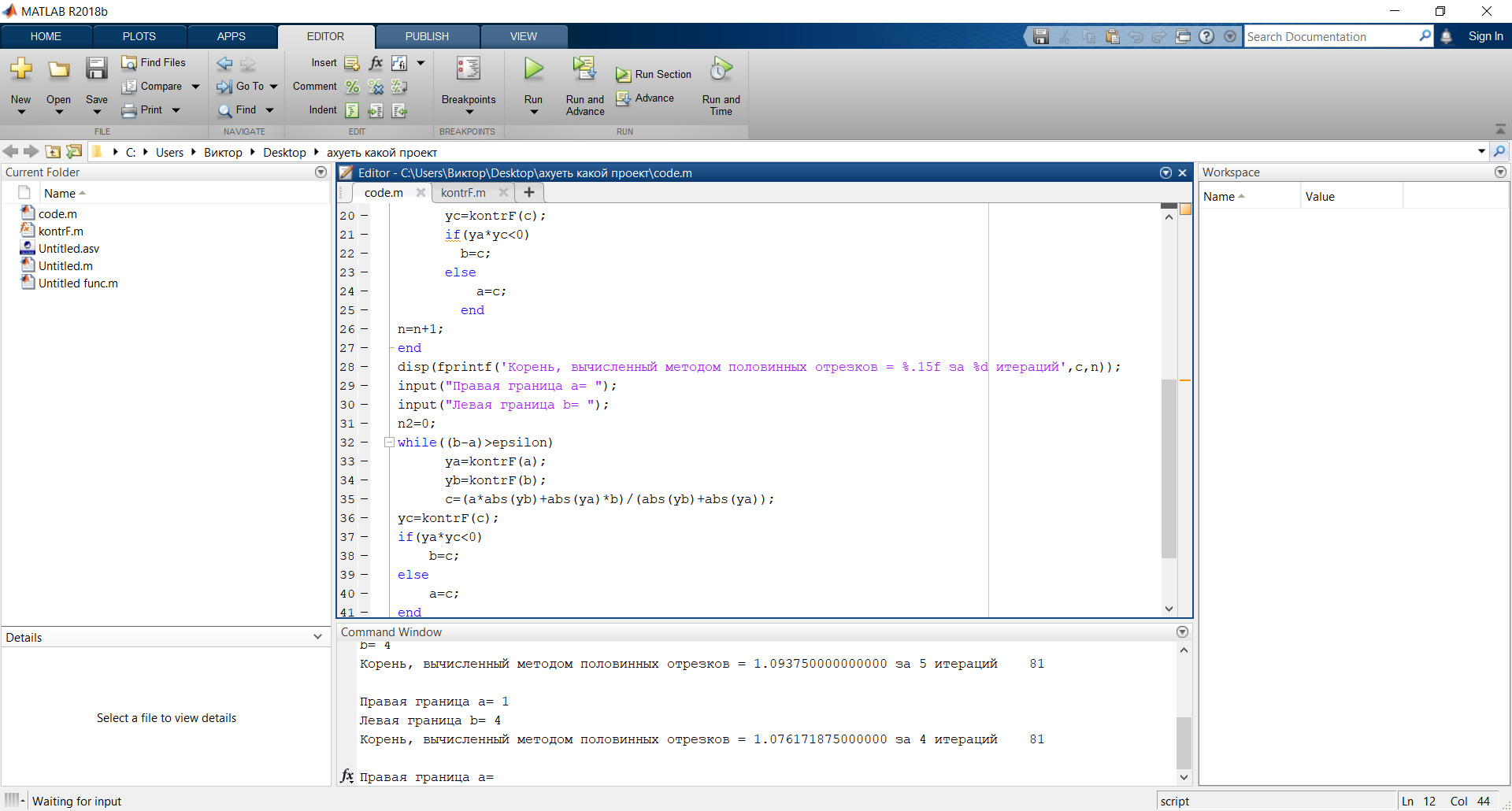                             Да Да Нет Нет b=c a=c n=n+1 ya*yc < 0 Конец c = (a+b)/2 ya=kontrF(a) yb=kontrF(b) yc=kontrF(c) Начало |b-a|>E a, b, f(x), E  Вывод корня и числа итераций Вывод: 1) С помощью MatLab был создан алгоритм поиска корней методом хорд и методом половинного деления. |
