шпоры озд. Первая лаб работа Интенсивный показатель явлениесреда Х100
 Скачать 326.71 Kb. Скачать 326.71 Kb.
|
|
Первая лаб работа: Интенсивный показатель: явление/среда Х100 Экстенсинвый показатель: часть явления/явление в целом Х100% Выводы: (примеры) а) анализ интенсивного показателя показывает, что самый высокий уровень (чего-то) приходится на возрастную группу..... Б) оценивая экстенсивный показатель можно сделать вывод, что наибольший удельный вес приходится на возрастную группу..... -Стобиковая диаграмма : ( интесивный показатель) Пример: Рис1.Повозрастная пладовитость женщин детородного возраста 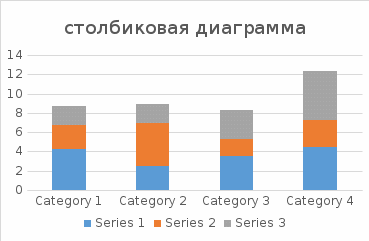 -Внутристолбиковая диаграмма: ( экстенсивный показатель) Пример: Рис2.Распределение живорожденных по возрасту матери 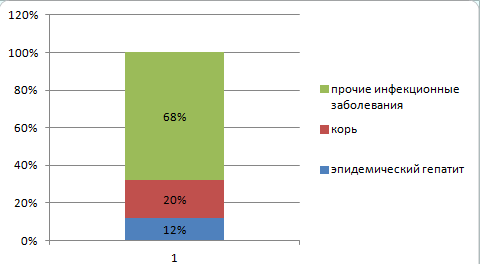 -секторная диаграмма: ( экстенсивный показатель): Пример: Рис3.Распределение живорожденных по возрасту матери 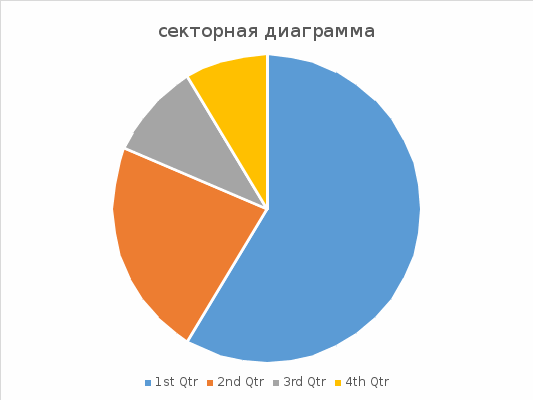 Вторая лаб работа: Мо(мода)= .... Ме(медиана)=....
средняя арефмитическая: М= Σv.p\n Среднне квадратическое отклонение: σ= ±√Σd2.p\n
Вывод:(пример):среднее квадратическое отклонение = 100% из этого следует, что средняя жилая площадь приходящаяся на одного человека в семье с низким уровнем достатка,составляющая 42% является типичной и ряд соответствует ряду с нормальным распеделением признака. Коэффициент вариации: (сv) Cv= σ\M X100% Если коэфициент вариации меньше 10% - малая степень колблемости От 10-20% средняя степень колеблемости Больше 20% высокая степень колеблемости Средняя ошибка средней арифметической: Mm= ± σ/√n Ошибка небольшая т.к показатель средней величины втрое ее превышает. Доверительные границы средней арифметической величины (в задаче этого вопроса не будет): А) Мген= Мвыб ±△, где △= tm t= 2 m= средняя ошибка средней арифметической С вероятностью безошибочного прогноза Р= 95.5% можно утверждать. Что средняя продолжительность не будет больше ...... и меньше ....... В) △= 3.m Мин= М ± △ С вероятностью безошибочного прогноза Р=99.7% можно утверждать, что средняя прдолж-ть будет больше ...... и меньше ...... (для себя) : Значения критерия Стьюдента (t) при числе наблюдений n>30: При t=2, достоверность Pt=95,5% и риск ошибки p<0,05; при t=2,6 Pt=99,0%, риск ошибки p<0,01; при t=3 Pt=99,7%, риск ошибки p<0,003; при t=3,3 Pt=99,9%, риск ошибки p<0,001. Третья лаб работа: 1 задача (вычислить частоту): А)Р= часть явления/явление в целом Х1000= Б)m = ± √p.q/n В) Рген= Р± tm Вывод: доверительные границы в пределах от ..... до...... и риск ошибки 0.05 2 задача: ( можно ли утверждать.....) t= M1-M2/√m1(2)-m2(2) Вывод: При t≥2 разность средних арифметических может быть признана существенной и не случайной, т.е. достоверной Надежность такого вывода будет не меньше 95,5%. При t < 2 достоверность разности средних величин считается недоказанной. Задача3: (вычислить относительные показатели.определите довтоверность разности) A)Р1= часть явление/явление в целом.1000= Б)Р2= часть явление/явление в целом.1000= В)mp1= ± √p.q/n Г) mp2= ±√p.q/n t= P1-P2/√m1(2)- m2(2) Вывод: Если t меньше 2, то разница недоказана Если t больше 2, то разница достоверная. Лаб работа 4 1)
Корреляция между .... и ......
1-Складывем все варианты x и y и делим их на количество наблюдений (n) 2-Для получения dx, dy отнимаем вышеполученный результат из каждой варианты 3-дальше умножаем dx,dy 4-Dx2 , dy2 Rxy= ± Σdx.dy/√Σdx2.Σdy2 Вывод: Величина коэффициента корреляции колеблется в пределах от 0 до 1. При rху = 0 связь отсутствует; при rху = 1 – связь полная. Если rху колеблется в пределах от 0 до 0,3 – связь слабая; от 0,3 до 0,7 – связь умеренная; от 0,7 до 1,0 – связь сильная. Знак (+) свидетельствует о наличии прямой (положительной) связи – когда с увеличением (уменьшением) значения одного признака увеличивается (уменьшается) значение другого, то есть, когда признаки меняются в одном направлении. Знак (-) свидетельствует об обратной (отрицательной) связи – когда с увеличением значения одного признака уменьшается значение другого и наоборот, то есть изменения признаков – разнонаправлены. 2) Средняя ошибка коэффициента корреляции: mr= √1-rxy2/n-2 tr= rxy/mr Лаб работа 5    |
