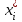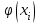РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА. Labra1111ГОТОВО. Первичная обработка статистических данных
 Скачать 206.45 Kb. Скачать 206.45 Kb.
|
3. Построение графиков теоретических плотности распределения и функции распределенияДля того, чтобы проверить гипотезу о том, что выборка из нормальной генеральной совокупности, подставим точечные оценки в место неизвестных параметров в плотность распределения вероятности и функцию распределения вероятности. Нормальная плотность распределения вероятности 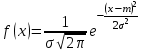 . . Будем считать, что 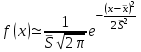 . . Результаты расчетов будем заносить в табл. 3. Сначала найдем  и занесем в третий столбец с округлением до сотых. и занесем в третий столбец с округлением до сотых.Далее по таблице ищем значения функции 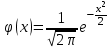 , соответствующие рассчитанным ранее значениям , соответствующие рассчитанным ранее значениям 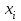 . При этом пользуемся четностью функции . При этом пользуемся четностью функции 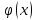 : : 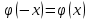 . Результат заносим в четвертый столбец табл. 3. . Результат заносим в четвертый столбец табл. 3.Найдем значения теоретической функции плотности вероятности 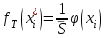 . Результат заносим в пятый столбец табл. 3. . Результат заносим в пятый столбец табл. 3.Находим значения теоретической функции распределения 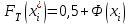 , где , где 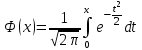 . Значения функции . Значения функции 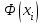 находятся по таблице с учетом того, что находятся по таблице с учетом того, что 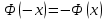 . Результаты заносим в последний столбец табл. 3. . Результаты заносим в последний столбец табл. 3.Табл. 3
Строим на основании расчетов графики теоретических плотности вероятности 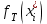 и функции вероятности и функции вероятности 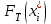 на рис. 1 и рис. 2 соответственно. на рис. 1 и рис. 2 соответственно.Вывод: Сравнивая графики теоретических и эмпирических функций, видим, что они достаточно хорошо согласованы. Следовательно, гипотеза о нормальном законе распределения вероятности генеральной совокупности правдоподобна. 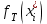  |