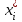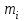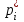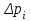РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА. Labra1111ГОТОВО. Первичная обработка статистических данных
 Скачать 206.45 Kb. Скачать 206.45 Kb.
|
4. Проверка гипотезы о нормальном распределении генеральной совокупностиМетодом Пирсона проверим гипотезу Н0 – генеральная совокупность распределена по нормальному закону. Альтернативная гипотеза НА – это не так. Результаты расчетов будем сводить в табл. 4. Критерий 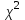 использует тот факт, что использует тот факт, что 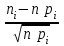 приближенно нормальная величина. Чтобы это условие выполнялось в достаточной мере, необходимо, чтобы в каждом интервале было не менее пяти точек. Для этого интервалы, в которых это условие не выполняется, следует объединить с соседними. Так, для данной выборки, это условие не выполняется в первом, втором, девятом и десятом интервалах (табл. 1). В табл. 4 первый и второй интервалы из табл. 1 объединены в один интервал, также объединены девятый и десятый интервалы табл. 1. приближенно нормальная величина. Чтобы это условие выполнялось в достаточной мере, необходимо, чтобы в каждом интервале было не менее пяти точек. Для этого интервалы, в которых это условие не выполняется, следует объединить с соседними. Так, для данной выборки, это условие не выполняется в первом, втором, девятом и десятом интервалах (табл. 1). В табл. 4 первый и второй интервалы из табл. 1 объединены в один интервал, также объединены девятый и десятый интервалы табл. 1. Определяем длину интервалов, середины, абсолютную и относительную частоты (аналогично тому, как это было сделано в первом пункте лабораторной работы). По результатам расчета заполняем первые шесть колонок табл. 4. Как это было сделано в третьем пункте, рассчитываем значения 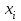 и и 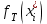 . Результаты заносим в седьмую и восьмую колонки табл. 4. . Результаты заносим в седьмую и восьмую колонки табл. 4.Ранее по выборке были найдены точечные оценки  и и 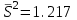 . Теперь оценим теоретические вероятности . Теперь оценим теоретические вероятности 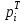 попадания нормальной случайной величины с указанными параметрами в интервал попадания нормальной случайной величины с указанными параметрами в интервал 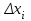 . .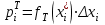 . . Заполняем девятую колонку табл. 4. Далее считаем 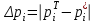 и заполняем десятую колонку табл. 4. и заполняем десятую колонку табл. 4.Значения 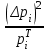 заносим в последний столбец табл. 4. заносим в последний столбец табл. 4.Табл. 4
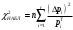 , здесь r – число интервалов табл. 4. Для данной выборки , здесь r – число интервалов табл. 4. Для данной выборки 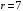 . .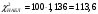 . . По таблице находим квантиль 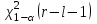 , где l – число оцениваемых параметров. В нашем случае , где l – число оцениваемых параметров. В нашем случае 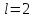 ( (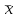 и и 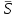 ). находим из условия ). находим из условия 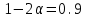 . .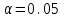 , , 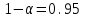 . . И так, по таблице находим 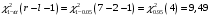 . .Если 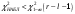 , то справедлива гипотеза Н0. Если , то справедлива гипотеза Н0. Если 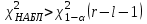 , то НА. В нашем случае , то НА. В нашем случае 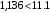 , то есть принимается гипотеза Н0. , то есть принимается гипотеза Н0.Вывод: Анализируя выборочные данные можно сделать вывод, подтвержденный с помощью критерия 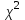 , что генеральная совокупность распределена по нормальному закону. , что генеральная совокупность распределена по нормальному закону. |