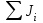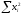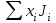Маятник Обербека. Пример_Маятник_Обербека. Первое высшее техническое учебное заведение россии министерство образованияя и науки российской федерации
 Скачать 135.22 Kb. Скачать 135.22 Kb.
|
|
ПЕРВОЕ ВЫСШЕЕ ТЕХНИЧЕСКОЕ УЧЕБНОЕ ЗАВЕДЕНИЕ РОССИИ  МИНИСТЕРСТВО ОБРАЗОВАНИЯЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «САНКТ-ПЕТЕРБУРГСКИЙ ГОРНЫЙ УНИВЕРСИТЕТ» Кафедра общей и технической физики. ОТЧЁТ ПО ЛАБОРАТОРНОЙ РАБОТЕ №6. По дисциплине: Физика (наименование учебной дисциплины согласно учебному плану) Тема: Определение момента инерции с помощью маятника Обербека. Автор: студент гр. РСК-17 / Стерхов И.А. / (подпись) (Ф.И.О) Оценка: Дата: Проверил: доцент / Ломакина Е.С. / (должность) (подпись) (Ф.И.О) Санкт-Петербург 2017 Цель работы: Исследовать зависимость момента инерции крестовины с надетыми на нее грузиками от распределения массы относительно оси вращения, проходящей через центр масс крестовины. Краткое теоретическое содержание: Момент инерции тела является мерой инертности тела при вращательном движении, подобно тому, как масса тела является мерой инертности тела при поступательном движении. Момент инерции тела зависит от распределения массы тела относительно оси вращения. Маятник Обербека состоит из крестовины, на стержнях которой находятся грузы. Они могут перемещаться по стержням и закрепляться в нужном положении. Крестовина с грузами насажена на вал, на котором укреплены два шкива различного радиуса. На шкив намотана нить, которая переброшена через блок. К ее концу привязана гирька, момент силы тяжести которой уравновешивает момент сил трения. К концу нити подвешивают груз массой m, под действием силы тяжести которого система приводится в движение. На груз действует сила тяжести P=mg и сила натяжения F, поэтому на основании второго закона Ньютона можно записать 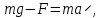 (1) (1)где g - ускорение свободного падения; а - ускорение, с которым движется груз. Крестовина приходит во вращательное движение под действием момента силы натяжения М = Frо , где rо - радиус шкива. Из приведенных уравнений можно получить: 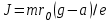 , (3) , (3)Так как угловое ускорение связано с ускорением а соотношением = а/r0 , то формулу (3) можно записать в виде 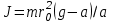 , (4) , (4)где а = 2h/t2; h - путь, пройденный грузом за время t. Таким образом, 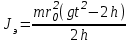 . (5) . (5)Из теоретических соображений следует, что момент инерции крестовины с четырьмя грузами массой 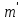 будет рассчитываться по следующей формуле: будет рассчитываться по следующей формуле: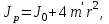 (6) (6)Необходимо переписать формулу (6) в виде 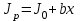 , (7) , (7)где r2 = х и 4m' = b. Метод наименьших квадратов позволяет найти J0 и b: 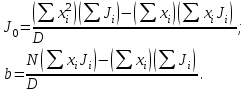 где 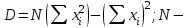 число опытов; Ji - экспериментальное значение момента инерции Jэ. число опытов; Ji - экспериментальное значение момента инерции Jэ.Среднее квадратичное отклонение: 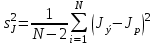 . .Явление, изучаемое в работе: Зависимость момента инерции от распределения массы относительно ос вращения. Схема установки:    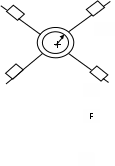 Где :  1 – крестовина 2 – грузы 3 – груз, массой m  4 – нить 5 – блок   Расчётные формулы для проведения эксперимента: 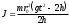 . где . где 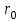 – радиус шкива, m- масса груза, h – путь, пройденный грузом – радиус шкива, m- масса груза, h – путь, пройденный грузом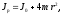 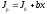 , где , где 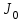 – момент инерции крестовины без грузов. – момент инерции крестовины без грузов. Среднее квадратичное отклонение 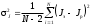 . .2. Формулы погрешности 1. 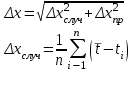 .2. 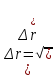 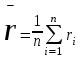 Таблица 1. (Постоянные данные)
Таблица 2 (Расчет момента инерции тела).
Таблица 3.
Вычисление всех необходимых величин для второго измерения: Среднее время: 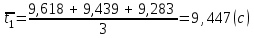 Момент инерции экспериментальный: 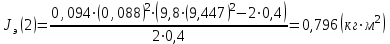 Момент инерции рассчитанный: 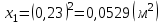 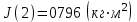  Вычисление среднего квадратичного отклонения: 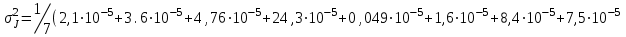 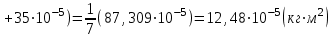 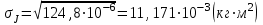  J 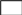 R2 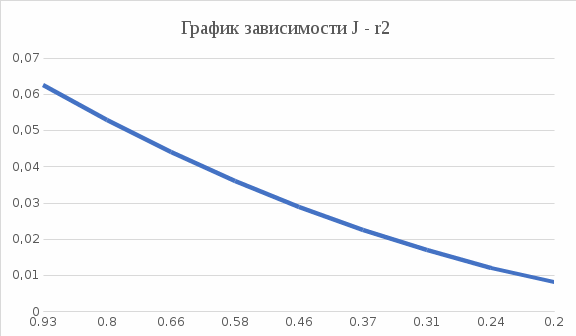 Вывод: В ходе выполнения лабораторной работы был рассчитан момент инерции для крестовины с надетыми на нее грузиками. Величина момента инерции рассчитана для каждого из восьми измерений (причем сам опыт был проделан 27 раз, но значения времени усреднялись по тройкам). Необходимо отметить, что момент инерции для этих измерений был получен двумя способами. Сравнение результатов при вычислении разными способами показало, что величины момента инерции, рассчитанные по-разному, имеют относительно небольшие различия между собой. Это подтверждено рассчитанным средним квадратичным отклонением: 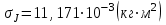 . Также был построен график зависимости момента инерции от квадрата радиуса. Следует отметить, что исходя из самой формулы нахождения момента инерции и непосредственно графика, зависимость между этими величинами прямо пропорциональны . Также был построен график зависимости момента инерции от квадрата радиуса. Следует отметить, что исходя из самой формулы нахождения момента инерции и непосредственно графика, зависимость между этими величинами прямо пропорциональны |

 , c
, c