РГЗ Первый курс. Первое высшее техническое учебное заведение россии министерство науки и высшего образования российской федерации федеральное государственное бюджетное образовательное учреждение высшего образования санктпетербургский горный университет
 Скачать 64.07 Kb. Скачать 64.07 Kb.
|
|
ПЕРВОЕ ВЫСШЕЕ ТЕХНИЧЕСКОЕ УЧЕБНОЕ ЗАВЕДЕНИЕ РОССИИ  МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ федеральное государственное бюджетное образовательное учреждение высшего образования САНКТ-ПЕТЕРБУРГСКИЙ ГОРНЫЙ УНИВЕРСИТЕТ Кафедра высшей математики Расчетно-графическое задание Вариант 9 По дисциплинеВысшая математика (наименование учебной дисциплины согласно учебному плану) Тема работы: Аналитическая геометрия и векторная алгебра Выполнила: студентка гр. ИГ-22-2 Жилко С.В. (шифр группы) (подпись) (Ф.И.О.) Оценка: Дата: Проверил руководитель работы: доцент Шабаева М.Б. (должность) (подпись) (Ф.И.О.)\ Санкт-Петербург 2022 В пространстве заданы четыре точки: А1(-14,-15,-8), А2(-2,11,11), А3(6,0,9), А4(-16,3,-20). Требуется выполнить следующие задания: Найти угол (косинус угла) между векторами 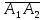 и и 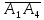 . .Решение: 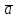 = = 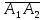 = {-2-(-14); 11-(-15); 11-(-8)} = {12; 26; 19} = {ax; ay; az} = {-2-(-14); 11-(-15); 11-(-8)} = {12; 26; 19} = {ax; ay; az}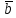 = = 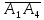 = {-16-(-14); 3-(-15); -20-(-8)} = {-2; 18; -12} = {bx; by; bz} = {-16-(-14); 3-(-15); -20-(-8)} = {-2; 18; -12} = {bx; by; bz}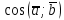 = = 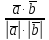 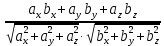 = = 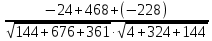 = = = = 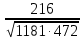 ≈ 0,29 ≈ 0,29∠ 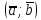 = arccos(0,29) = arccos(0,29)Ответ:∠ 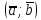 = arccos(0,29) = arccos(0,29)Найти S – площадь треугольника А1А2А3 (с помощью векторного произведения). Проверить, что вектор 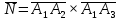 перпендикулярен векторам перпендикулярен векторам 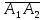 и и 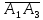 . .Решение: Найдем координаты векторов 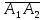 и и 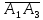 : :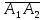 = {12; 26; 19} = {12; 26; 19}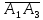 = {6-(-14); 0-(-15); 9-(-8)} = {20; 15; 17} = {6-(-14); 0-(-15); 9-(-8)} = {20; 15; 17}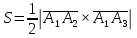 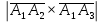 = = 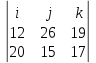 = 157i+176j-340k = 157i+176j-340k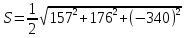 ≈ 206,89 (ед.кв) ≈ 206,89 (ед.кв)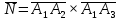 = {157; 176; -340} = {157; 176; -340}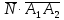 = 157 = 157 12+176 12+176 26+ (-340) 26+ (-340) 19 = 0 ⇒ 19 = 0 ⇒ 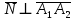 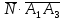 = 157 = 157 20+176 20+176 15+ (-340) 15+ (-340) 17 = 0 ⇒ 17 = 0 ⇒ 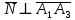 Ответ: S = 206,89 ед.кв. Найти V – объем пирамиды А1А2А3А4 (с помощью смешанного произведения). Решение: Найдем координаты векторов 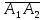 и и 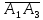 : :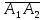 = {12; 26; 19} = {12; 26; 19}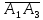 = {20; 15; 17} = {20; 15; 17}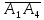 = {-2; 18; -12} = {-2; 18; -12}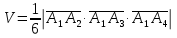 = =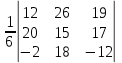 = = 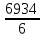 ≈ 1155,67 (ед.куб.) ≈ 1155,67 (ед.куб.)Ответ:V =1155,67 ед.куб. Составить общее уравнение плоскости, проходящей через точки А1, А2, А3 (в качестве нормали к плоскости взять вектор 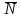 , найденный в пункте 2). Проверить, что все три точки принадлежат этой плоскости. , найденный в пункте 2). Проверить, что все три точки принадлежат этой плоскости.Решение: Пусть плоскость, проходящая через точки А1, А2, А3 – плоскость 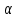 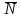 = {157; 176; -340} - нормаль к плоскости = {157; 176; -340} - нормаль к плоскости 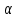 А1(-14,-15,-8), А2(-2,11,11), А3(6,0,9) Общее уравнение плоскости 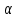 : 157(x-(-14)) + 176(y-(-15)) - 340(z-(-8))) = 0 : 157(x-(-14)) + 176(y-(-15)) - 340(z-(-8))) = 0157x + 176y - 340z +2118 = 0 Подставим точку А1 в общее уравнение плоскости 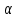 : :157(-14) + 176(-15) - 340(-8) +2118 = 0⇒ А1 ∈ 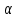 Подставим точку А2 в общее уравнение плоскости 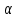 : :157(-2) + 176(11) - 340(11) +2118 = 0⇒ А2 ∈ 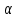 Подставим точку А3 в общее уравнение плоскости 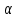 : :157(6) + 176(0) - 340(9) +2118 = 0⇒ А3 ∈ 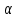 Ответ:157x + 176y - 340z +2118 = 0 Найти угол (синус угла) между ребром А1А4 и плоскостью А1А2А3. Решение: 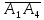 = {-2; 18; -12} = {-2; 18; -12}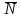 = {157; 176; -340} = {157; 176; -340}sin ( 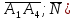 = = 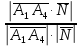 = = 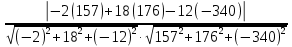 ≈ 0,77 ≈ 0,77∠( 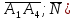 = arcsin(0,77) = arcsin(0,77)Ответ:∠( 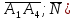 = arcsin(0,77) = arcsin(0,77)Составить канонические уравнения высоты, опущенной из вершины А4 на основание А1А2А3. Решение: А4(-16,3,-20) 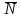 = {157; 176; -340} = {157; 176; -340}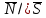 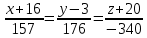 –канонические уравнения высоты –канонические уравнения высотыОтвет: 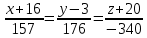 Найти h – расстояние от точки А4 до А1А2А3 с помощью формулы расстояния от точки до плоскости. Убедиться, что V = 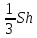 (см. пп. 2 и 3). (см. пп. 2 и 3).Решение: 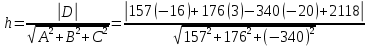 ≈ 16,76 ≈ 16,76V = 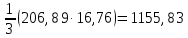 A1A2A3: 157x + 176y - 340z +2118 = 0 Ответ:h = 16,76 Найти d – расстояние от точки А4 до прямой А1А2 с помощью формулы расстояния от точки до прямой. Решение: 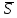 = {12; 26; 19} = {12; 26; 19}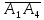 = {-2; 18; -12} = {-2; 18; -12}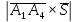 = = 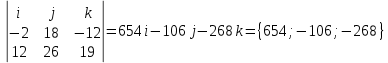 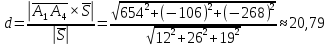 Ответ:d = 20,79 |
