Первое высшее техническое учебное заведение россии министерство науки и высшего образования российской федерации
 Скачать 130.12 Kb. Скачать 130.12 Kb.
|
|
ПЕРВОЕ ВЫСШЕЕ ТЕХНИЧЕСКОЕ УЧЕБНОЕ ЗАВЕДЕНИЕ РОССИИ  МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ федеральное государственное бюджетное образовательное учреждение высшего образования «САНКТ-ПЕТЕРБУРГСКИЙ ГОРНЫЙ УНИВЕРСИТЕТ» ОТЧЕТ Расчетно-графическое задание №4 Вариант №1
Санкт-Петербург 2021 год Задание 1: По двум последним цифрам шифра студента (…ab) определяется вариационный ряд из двадцати значений (с шагом h = 3) и соответствующих частот: 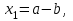 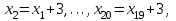 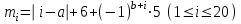 . .Произвести группировку значений и по сгруппированному вариационному ряду построить эмпирическую функцию распределения и гистограмму. Данные: ab=1+30(2-1)=31 a=3 b=1 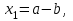 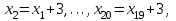 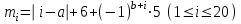 Решение: Подставим данные.
Объем выборки: n= 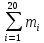 n=276 Размах выборки: 57 Вводим интервалы группировки: 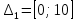 (чтобы первое значение x1=2 включалось с запасом), (чтобы первое значение x1=2 включалось с запасом),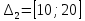 , ,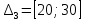 , ,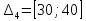 , ,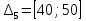 , ,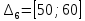 , , 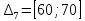 (последнее значение x20=59 включается с запасом). Для сгруппированного вариационного ряда значения равны серединам интервалов: (последнее значение x20=59 включается с запасом). Для сгруппированного вариационного ряда значения равны серединам интервалов: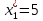 , , 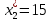 , , 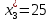 , , 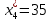 , , 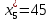 , , 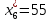 , ,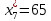 а частоты а частоты 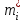 для этих значений (т.е. для интервалов для этих значений (т.е. для интервалов 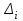 ) получаем, складывая частоты значений ) получаем, складывая частоты значений 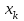 , попавшие в соответствующий интервал , попавшие в соответствующий интервал 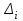 группировки, причем для значения группировки, причем для значения 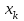 , попавшего на границу двух интервалов, частота , попавшего на границу двух интервалов, частота 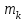 делится между этими интервалами поровну: делится между этими интервалами поровну: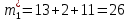 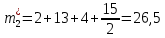 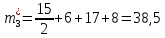 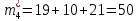 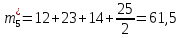 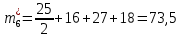 Эмпирические вероятности равны: 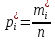 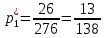 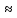 0,094 0,094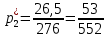  0,096 0,096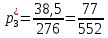  0,139 0,139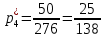  0,181 0,181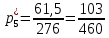  0,224 0,224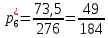 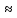 0,266 0,266Отметим, что 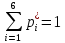 . .Накопленные вероятности: За 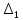 : :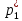 =0,094; за =0,094; за 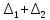 : :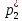 =0,19; за =0,19; за 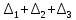 : :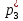 =0,329; за =0,329; за 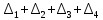 : :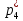 =0,51; за =0,51; за 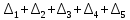 : :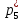 =0,734; за =0,734; за 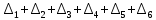 : :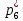 =1 =1 Определяем эмпирические плотности: 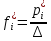 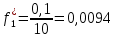 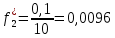 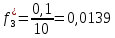 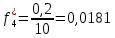 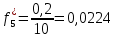 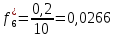 Графики Задание 2: Сгруппированный вариационный ряд задан серединами интервалов xi и соответствующими частотами mi. Восстановить интервалы и оценить с помощью критерия Пирсона хи-квадрат согласие данных с нормальным распределением при уровне значимости 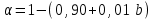 , где b – последняя цифра шифра. , где b – последняя цифра шифра.Данные:
b=9 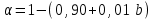 Решение: a=1-(0,9+0,01)=0,09 Данные интервалы: 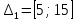 ; ; 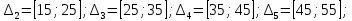 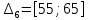 Введем условную варианту, определив шаг h=10 и выбрав ложный нуль C=30, и найдем 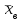 и и 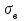
По данный таблицы имеем n=50 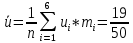 => =>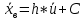 =10* =10*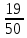 +30=33,8 +30=33,8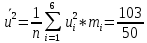 => =>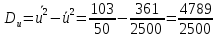 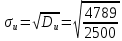 = =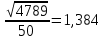 => =>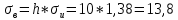 Найдем теоретические частоты для интервала 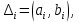 используя формулу вероятности попадания значений в этот интервал (для нормального распределения с параметрами используя формулу вероятности попадания значений в этот интервал (для нормального распределения с параметрами 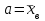 и и 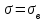 ): ):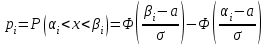 . .
Найдем выборочное значение 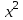 , объединив крайние интервалы для маленьких частот mi. , объединив крайние интервалы для маленьких частот mi.
X2= 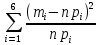 =2,31 =2,31Таким образом, если после объединения число интервалов 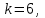 а число наложенных связей p=3, то число степеней свободы r=k-p=6-3=3. Поэтому по таблице критических значений а число наложенных связей p=3, то число степеней свободы r=k-p=6-3=3. Поэтому по таблице критических значений 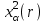 имеем имеем 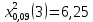 . Сравнивая найденное значение X2=2,31 с критическим (2,31<6,25), определяем, что рассматриваемые данные можно считать полученными из нормально распределенной совокупности. . Сравнивая найденное значение X2=2,31 с критическим (2,31<6,25), определяем, что рассматриваемые данные можно считать полученными из нормально распределенной совокупности.Задание 3: Найти выборочные регрессии, построить их графики и точки условных средних на одном чертеже. Оценить качество связи. Данные: ab=31
Решение:
Для определения выборочных регрессий перейдем к условным вариантам. Наибольшая частота, ближайшая к центру таблицы, m43=26 и, следовательно, соответствующие ложные нули C1=x4=30 и C2=y3=23 шаг h1=7 (для xi) и 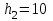 (для yj). (для yj).Составим новую таблицу в условных вариантах для расчета характеристик:
По данным таблицы получим выборочные характеристики: 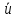 = =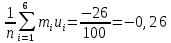 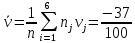 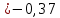 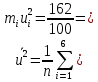 1,62 1,62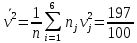 =1,97 =1,97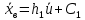 =7*(-0,26)+30 =7*(-0,26)+30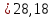 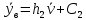 =10*(-0,37)+23 =10*(-0,37)+23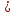 20,41 20,41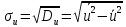 = = 1,24595=> 1,24595=>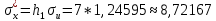 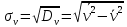 = =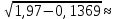 1,35392=> 1,35392=>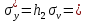 10*1,35392 10*1,35392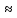 13,5392 13,5392Для вычисления 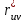 найдем средние суммы всех произведений uivjmij: найдем средние суммы всех произведений uivjmij: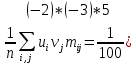 +(-2)*(-2)*7+(-2)*0*14+(-1)*(-1)*2+ +(-2)*(-2)*7+(-2)*0*14+(-1)*(-1)*2++(-1)*1*18+(-1)*2*4+0*0*26+1*(-2)*5+1*(-1)*3+1*1*2+2*(-3)*1+2* *(-2)*4+2*0*9+2*1*1]= 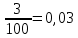 Выборочный коэффициент корреляции 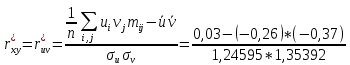 =-0,03924 =-0,03924Уравнения выборочных регрессий имеют вид для регрессии Y на X y- 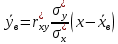 => y-20,41 => y-20,41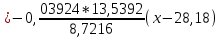 y=-0,06092x+22,12659 Для регрессии X на Y x- 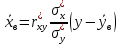 =>x-28,18 =>x-28,18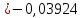 * *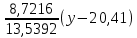 x=-0,025277у+28,69591 Обе регрессии проходят через точку средних ( 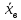 ; ;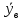 )=(28,18; 20,41) и для построения прямых найдем еще по одной точке для каждой прямой. )=(28,18; 20,41) и для построения прямых найдем еще по одной точке для каждой прямой.Для y=-0,164301x+27,28595 это точка (0; 27,28595), для прямой x=-0,09066у+26,37247 это точка (26,37247;0). Так как |r*xy|=0,03924 далеко от нуля (угол между прямыми наилучших линейных регрессий близких к нулю), то связь между изучаемыми случайными величинами достаточно сильная, и т.к. далек от единицы, то связь сильно линейная. График: | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

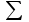
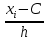
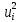
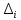
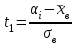
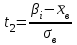
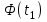
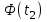
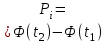
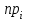
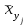
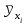
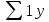 =
=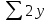 =197
=197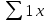 =
=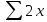 =162
=162