Первообразная функция
 Скачать 1.62 Mb. Скачать 1.62 Mb.
|
§ 1 Способы и примеры решения первообразной функцииФункция 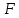 называется первообразной для функции называется первообразной для функции 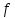 на заданном промежутке, если для всех на заданном промежутке, если для всех 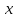 из этого промежутка из этого промежутка 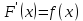 [1 c. 291]. [1 c. 291].Пример 1. Функция 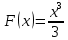 есть первообразная для функции есть первообразная для функции 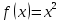 на интервале на интервале 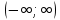 , так как , так как 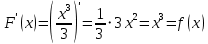 для всех для всех 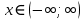 . .Легко заметить, что 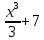 имеет ту же самую производную имеет ту же самую производную 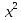 и поэтому также является первообразной для и поэтому также является первообразной для 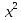 на на 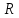 . Ясно, что вместо числа . Ясно, что вместо числа 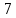 можно поставить любую постоянную. Таким образом, мы видим, что задача нахождения первообразной имеет бесконечно много решений. можно поставить любую постоянную. Таким образом, мы видим, что задача нахождения первообразной имеет бесконечно много решений.Пример 2. Для функции 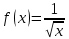 на интервале на интервале 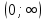 первообразной является функция первообразной является функция 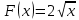 , так как , так как 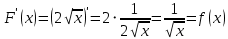 для всех для всех 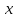 из этого интервала. Функция из этого интервала. Функция 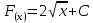 при любой постоянной при любой постоянной 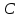 есть первообразная для функции есть первообразная для функции 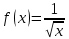 на том же интервале на том же интервале 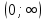 . .Пример 3. Функция 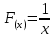 не является первообразной для функции не является первообразной для функции 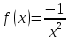 на промежутке на промежутке 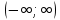 , так как равенство , так как равенство 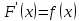 не выполнено в точке не выполнено в точке 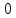 . Однако в каждом из промежутков . Однако в каждом из промежутков 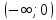 и и 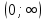 функция функция 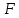 является первообразной для является первообразной для 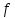 . .Таблица первообразных (Рис. 1) 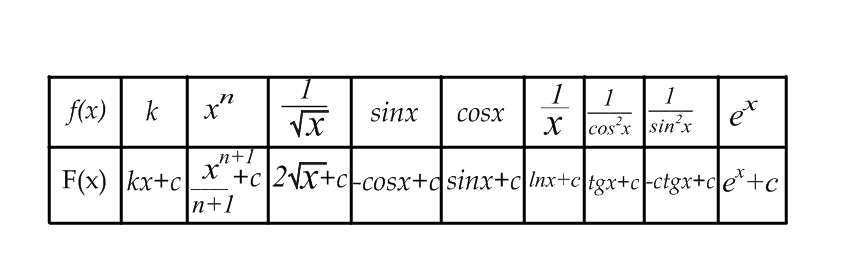 Рис. 1 Три правила нахождения первообразных: правило 1. Если 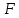 есть первообразная для есть первообразная для 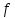 , а , а 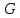 – первообразная для – первообразная для 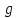 , то , то 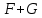 есть первообразная для есть первообразная для 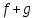 [1 c. 295]. [1 c. 295].Правило 2. Если 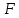 есть первообразная для есть первообразная для 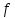 , а , а 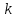 – постоянная, то – постоянная, то 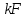 – первообразна для – первообразна для 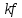 [1 c. 295]. [1 c. 295].Правило 3. Если 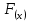 есть первообразная для есть первообразная для 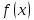 , а , а 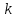 и и 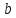 – постоянные, причем – постоянные, причем 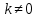 , то , то 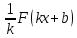 есть первообразная для есть первообразная для 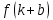 [1 c. 295]. [1 c. 295].Пример 1. Найдем общий вид первообразных для функции 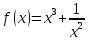 . Так как для . Так как для 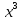 одна из первообразных есть одна из первообразных есть 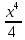 , а для , а для 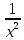 одной из первообразных является – одной из первообразных является – 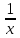 , по правилу 1 находим: одной из первообразных для функции , по правилу 1 находим: одной из первообразных для функции 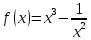 будет будет 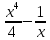 . .Ответ. 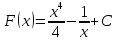 . .Пример 2. Найдем одну из первообразных для функции 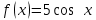 . Так как для . Так как для 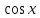 одна из первообразных есть одна из первообразных есть 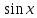 , применяя правило 2, получаем ответ: , применяя правило 2, получаем ответ: 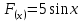 . .Пример 3. Найдем одну из первообразных для функции 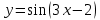 . Для . Для 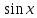 одной их первообразных является – одной их первообразных является – 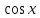 , поэтому по правилу 3 искомая первообразная равна , поэтому по правилу 3 искомая первообразная равна 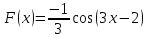 . .Фигура, ограниченная графиком непрерывной неотрицательной на отрезке [a;b]функции f(x) и прямыми y=0, x=a и x=bx=b, называется криволинейной трапецией[1 c. 298]. Площадь криволинейной трапеции вычисляется по формуле: S= 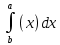 [1 c. 298].(1) [1 c. 298].(1)Задачи на нахождение площади криволинейной трапеции мы будем условно делить на 4 типа. Рассмотрим каждый тип подробнее. I тип: криволинейная трапеция задана явно. Тогда сразу применяем формулу (1). Например, найти площадь криволинейной трапеции, ограниченной графиком функции y=4−(x−2)2, и прямыми y=0, x=1 и x=3x=3. Нарисуем эту криволинейную трапецию (Рис.2). 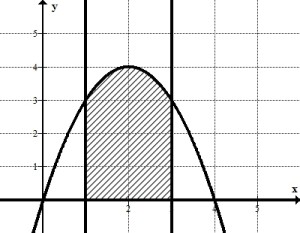 Рис.2 Применяя формулу (1), найдём площадь этой криволинейной трапеции. S=∫13(4−(x−2)2)dx=∫134dx−∫13(x−2)2dx=4x|13−(x−2)33|13= =4(3−1)−13((3−2)3−(1−2)3)=4⋅2−13((1)3−(−1)3)=8−13(1+1)= =8−23=713 (2). II тип: криволинейная трапеция задана неявно. У этого случая обычно не задаются или задаются частично прямые x=a, x=bx=a, x=b. В этом случае нужно найти точки пересечения функций y=f(x) и y=0y=0. Эти точки и будут точками a и b. Например, найти площадь фигуры, ограниченной графиками функций y=1−x2и y=0y=0. Найдём точки пересечения. Для этого приравняем правые части функций. 1−x2=0 x2=1 x=±1 Таким образом, a=−1, а b=1. Нарисуем эту криволинейную трапецию(Рис.3) 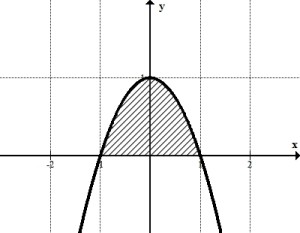 Рис.3 Найдём площадь этой криволинейной трапеции. S=∫−11(1−x2)dx=∫−111dx−∫−11x2dx=x|−11−x33|−11= =(1−(−1))−13(13−(−1)3)=2−13(1+1)=2−23=113 III тип: площадь фигуры, ограниченной пересечением двух непрерывных неотрицательных функций. Эта фигура не будет криволинейной трапецией, а значит с помощью формулы (1) её площадь не вычислишь. Как же быть?Оказывается, площадь этой фигуры можно найти как разность площадей криволинейных трапеций, ограниченных верхней функцией и y=0 (3), и нижней функцией и y=0 (4), где в роли x=a, x=b выступают координаты по x точек пересечения данных функций, т.е. S=(3)−(4). (5) Самое главное при вычислении таких площадей − не "промахнуться" с выбором верхней и нижней функции. Например, найти площадь фигуры, ограниченной функциями у=x2 и y=x+6. Найдём точки пересечения этих графиков: x2=x+6 x2−x−6=0 По теореме Виета, x1=−2, x2=3. То есть, a=−2, b=3. Изобразим фигуру(Рис.4) 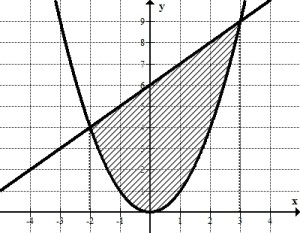 Рис.4 Таким образом, верхняя функция - y=x+6, а нижняя -y=x2. Далее, найдём (3) и (4) по формуле (1). (3) =∫−23(x+6)dx=∫−23xdx+∫−236dx=x22∣∣3−2+6x|3−2= =32,5(2). (4) =∫−23x2dx=x33∣∣3−2=353(4)=∫−23x2dx=x33|−23=353 (2). Подставим найденное в (5) и получим: S=32,5−353=1256S=32,5−353=1256 (2). IV тип: площадь фигуры, ограниченной функцией (-ями), не удовлетворяющей(-ими) условию неотрицательности. Для того, чтобы найти площадь такой фигуры нужно симметрично относительно оси Ox (иными словами, поставить "минусы" перед функциями) отобразить область и с помощью способов, изложенных в типах I - III, найти площадь отображённой области. Эта площадь и будет искомой площадью. Предварительно, возможно, вам придётся найти точки пересечения графиков функций. Например, найти площадь фигуры, ограниченной графиками функций y=x2−1 и y=0. Найдём точки пересечения графиков функций: x2−1=0. x=±1, т.е. a=−1, а b=1. Начертим область(Рис.5) 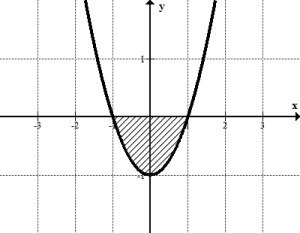 Рис.5 Симметрично отобразим область: y=0 ⇒ y=−0=0 y=x2−1 ⇒ y=−(x2−1)=1−x2y=x2−1 ⇒ y=−(x2−1)=1−x2. Получится криволинейная трапеция, ограниченная графиком функции y=1−x2 и y=0. Это задача на нахождение криволинейной трапеции второго типа. Она была рассмотрена выше. Ответ был такой: S=113(2). Значит, площадь искомой криволинейной трапеции равна: S=113(2). |
