Первообразная функция
 Скачать 1.62 Mb. Скачать 1.62 Mb.
|
§ 3. Этапы создания элементов дистанционного курса в системе LMS Moodle по теме «Первообразная функция»Работу в системе LMS Moodle начнем с входа в систему.  После входа мы переходим на страницу пользователя.  Создаем курс с названием «Первообразная функция». Добавляем определение, две лекции и тест.  В лекции «Первообразная функця» у нас будет четыре страницы. Первая будет называться «Краткая история первообразной функции». Вторая страница лекции будет для таблицы производной. Третью оставим для краткой теории и примеров решения. Четвертую выделим для трех правил нахождения первообразных. Переходим к первой страницы и добавляем материал.  Добавляем кнопку вперед.  Сохраняем страницу и переходим к следующей. Вставляем заранее подготовленную таблицу и настраиваем размеры картинки. 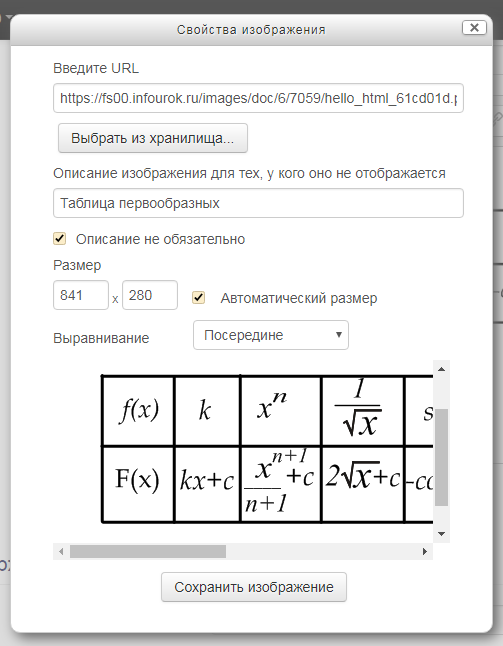 Сохраняем изображение, добавляем кнопки вперед, назад и переходим к следующей странице. В названии страницы пишем «Краткая теория и примери решения». Вставляем материал и кнопки. Сохраняем страницу. 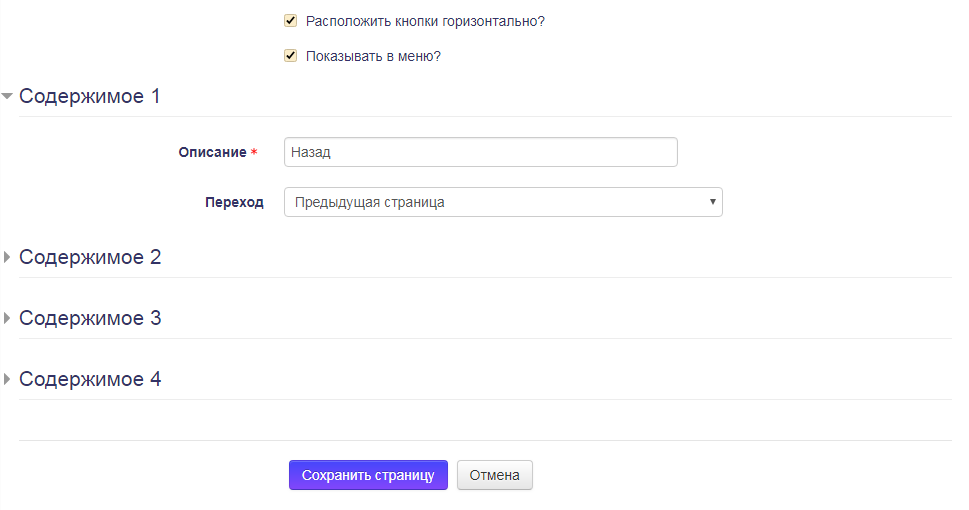 Четвертую страницу делаем по тому принципу, что и третью, но добавляем еще одну кнопку «Вначало».  Сохраняем лекцию и переходим к другой. В данной лекции у нас будет три страницы. Добавим первую информационную страницу и оглавление раздела.  Далее как и в третьей и четвертой станице первой лекции.  Вторую и третью страницу делаем по принципу первой старицы этой лекции. 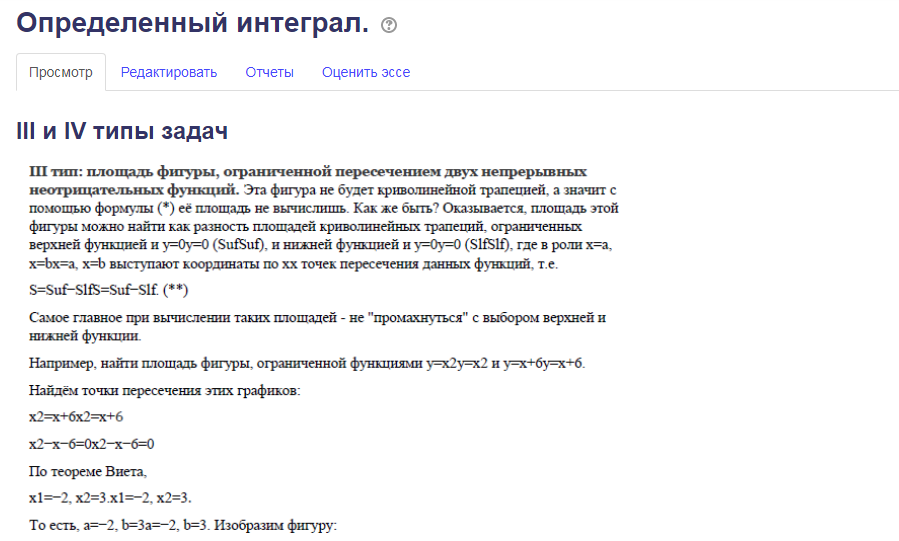  Теперь переходим к тесту. Выбираем редактировать тест.  Добавляем вопрос. Пишем название цифрой и текст вопроса.  Вводим варианты ответов. Где правильный вариант ставим оценку 100%.  Так делаем и остальные вопросы в тесте. Просмартиваем весь тест и проверяем на наличие ошибок, если таковых не обнаружено сохраняем тест.  Проверяем весь курс. После проверки мы смело можем сказать, что наш конечный продукт готов. ЗаключениеВ ходе работы над проектом были изучены и систематизированы материалы книги Дмитрия Орловского Германович «Неопределенный интеграл» и учебника Алимова Шавката Арифжданович «Алгебра и начала анализа», интернет-сайтов: Лекция по теме первообразная функция и её свойства, 100ballov.kz образовательный портал для учеников и студентов по теме первообразная функция и основное свойство первообразной и Национальный исследовательский Томский политехнический университет по теме MOODLE. В данной работе мы охарактеризовали способы и примеры решения первообразной функции, определили принципы работы LMS Moodle и описали этапы создания дистанционного курса. Наш продукт может использоваться для дистанционного домашнего изучения первообразной функции и для проверки знаний студентов. Список литературы1. Алгебра и начала анализа: учебник для 10-11 классов общеобразовательных учреждений / Ш. А. Алимов, Ю. М. Колягин, Ю. В. Сидоров. М.: Просвещение, 2012. – 384 с. URL: http://vklasse.org/11-klass/uchebniki/algebra/sha-alimov-yum-kolyagin-mv-tkacheva-2012/stranitsa-0 (дата обращения 07.02.18). 2. Орловский Д. Г. Неопределенный интеграл. Практикум: Учебное пособие. – СПб.: Издательство «Лань», 2014. – 432 с. URL: https://vk.com/doc331117905_459281448?hash=10fc654a5777dcb0c2&dl=b53d722fcb0e6acfaa (дата обращения 07.02.18). 3. Первообразная функция и её свойства [Электронный ресурс] // Интернет-сайт «Лекция». URL: https://lektsia.com/4x2c6.html (дата обращения 27.12.17). 4. Первообразная функция. Основное свойство первообразной [Электронный ресурс] // Интернет-сайт «100ballov.kz образовательный портал для учеников и студентов». URL: http://100ballov.kz/mod/page/view.php?id=800 (дата обращения 27.12.17). 5. MOODLE [Электронный ресурс] // Интернет-сайт «Национальный исследовательский Томский политехнический университет». URL: http://portal.tpu.ru/eL/system_elearning_TPU/moodle (дата обращения 27.12.17). |
