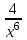|
|
интеграл. Поурочный план урока 62. Первообразная и неопределенный интеграл
«Геологиялық барлау колледжі» КМҚК
КГКП «Геологоразведочный колледж»
№ 62сабақ жоспары
Поурочный план № 62.
Сабақтың тақырыбы
Тема урока
|
Первообразная и неопределенный интеграл
|
Курс, топ
Курс, группа
|
1 курс. Ос-01, Г-01а, Б-01.
|
Модульдің атауы/пән
Наименование модуля/дисциплины
|
Математика
|
Оқытушы
Преподаватель
|
Адылханова.С.К
|
Мерзімі
Дата
|
08.02.-12.02. 2021.
|
Сабақтың типі
Тип урока
|
Комбинированный
|
Сабақтың оқу мақсаттары
Цели обучения
|
Обучающиеся будут уметь: сформировать и закрепить понятие первообразной, находить первообразные функции разного уровня. применять теоретический материал при решении задач.
|
Бағалау критерийлері
Критерии оценивания
|
Обучающийся достиг цели, если:
знать: - определение производной
- первообразная определяется неоднозначно.
уметь: находить первообразные функции в простейших случаях
- проверять, является ли первообразная для функции на данном промежутке времени.
|
Оқу-әдістемелік, техникалық жабдықтау, анықтамалық әдебиет
Учебно-методическое, техническое оснащение, справочная литература
|
1.Абылкасымова А., Жумагулова З. Алгебра и начала анализа.
Учебник для 10 классов обшественно-гуманитарного направления обшеобразовательных школ. Алматы: Мектеп, 2019г.
Ноутбук, презентация по теме.
|
Пәнаралық байланыстар
Межпредметные связи:
|
У обучающихся закладываются базовые знания в определении понятия производной.
|
Сабақтың барысы
Ход урока
Жоспарланған мерзімдер
Планируемые сроки
|
Жоспарланған әрекеттер
Планируемые действия
|
Ресурстар
Ресурсы
|
. Начало урока:
0-1 мин
|
1. Ұйымдастыру кезеңі
1. Организационный момент. Приветствие, проверить готовность учащихся к уроку. Ознакомление с целью
|
|
Сабақтың басталуы
Начало урока 2-10 мин.
|
2. Білімді өзектендіру
2. Актуализация знаний. Устный опрос правил и определений:
1. Новые знания нам будет очень трудно осваивать без повторения некоторых вопросов (слайды №1).
2.Мотивация.
1. В чем состоит геометрический смысл производной функции.
2. В чем состоит механический смысл производной функции.
3. Дайте определение производной функции f(x) в точке х0
4. Основные формулы дифференцирования.
5. Уравнение касательной к графику функции.
|
-Рабочие тетради,
-Учебник,
Презентация
|
. Жаңа материалды түсіндіру
3. Изучение нового материала.
2. Изучение нового материала.
2.Введение новых понятий и алгоритмов.
1 Тема сегодняшнего занятия «Неопределенный интеграл и его свойства». Знания по данной теме нами будет использоваться на следующих уроках при нахождении определенных интегралов, площадей плоских фигур. Большое внимание уделяется интегральному исчислению в разделах высшей математики в высших учебных заведениях при решении прикладных задач.
Наше сегодняшнее занятие является занятием изучения нового материала, по этому будет носить теоретический характер. Цель занятия сформировать представления об интегральном исчислении, понять его сущность, развивать навыки при нахождении первообразных и неопределенного интеграла.
 Задача 1. Закон движения тела Задача 1. Закон движения тела 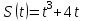 , найти его мгновенную скорость в любой момент времени. , найти его мгновенную скорость в любой момент времени.
 Задача 2. Зная скорость движущегося тела в каждый момент времени Задача 2. Зная скорость движущегося тела в каждый момент времени 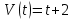 , найти закон его движения. , найти закон его движения.
Возможно ли решить задачу используя имеющиеся у нас средства ? (Создание проблемной ситуации ).
Предположения учащихся :
- Для решения этой задачи необходимо ввести операцию, обратную дифференцированию.
- Операция дифференцирования сопоставляет заданной функции F (x) ее производную.
 . .
- Исходя из данной функции f (x) , найти такую функцию F (x) производной которой является f (x) , т.е. 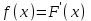 . .
А) Взаимно-обратные операции в математике.
В математике существуют 2 взаимно-обратные операции в математике. Рассмотрим в сравнении.
ПРЯМАЯ.
|
ОБРАТНАЯ.
|
Сложение
Умножение
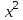 - возведение в квадрат. - возведение в квадрат.
|
Вычитание
Деление
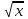 - извлечение из квадратного корня. - извлечение из квадратного корня.
|
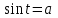 - синус угла. - синус угла.
…………………………..
|
 - арксинус угла. - арксинус угла.
………………………………
|
дифференцирование
вычисление производной
|
интегрирование
восстановление функции из производной
|
Б) Взаимно-обратные операции в физике.
Рассматриваются две взаимно-обратные задачи в разделе механике. Нахождение скорости по заданному уравнению движения материальной точки (нахождение производной функции) и нахождение уравнения траектория движения по известной формуле скорости.
***Производная – «производит» на свет новую функцию. Первообразная - первичный образ.
Определение первообразной, её основное свойство, правила нахождения первообразных.
Определение 1. Функцию F (x) , заданную на некотором промежутке X, называют первообразной для функции задан ной на том же промежутке, если для всех x  X выполняется равенство X выполняется равенство  . .
 Найти первообразные функций: Найти первообразные функций:
1) 
2) 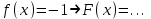
3) 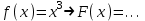
4) 
5) 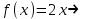 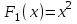 , проверка: , проверка: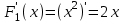
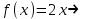 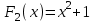 , проверка: , проверка: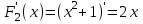
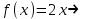 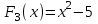 , проверка: , проверка:
Теорема (о неоднозначности первообразной): y = f(x) имеет бесконечно много первообразных вида y = F(x)+C, где C - произвольное число.
С геометрической точки зрения это означает, что графики любых двух первообразных для функции 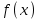 получаются друг из друга параллельным переносом вдоль оси Oy. получаются друг из друга параллельным переносом вдоль оси Oy.
Свойство 1. Если F есть первообразная для функции f, а G – первообразная для g, то F+G – есть первообразная для f+g.

Пример. 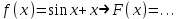
Свойство 2. Если F – первообразная для f, а k – постоянная, то функция kF – первообразная для kf.
Пример. 
Свойство 3. Если F – первообразная для f, а k и b– постоянные ( ), то функция ), то функция 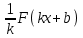 - первообразная для f(kx+b). - первообразная для f(kx+b).
Пример. 
Понятие неопределенного интеграла, его свойства. О происхождении терминов и обозначений.
Определение: Неопределенным интегралом от функции y = f(x) называется совокупность первообразных F(x)+C, т.е.  , где функциюf(x) называетсяподынтегральной функцией, а выражение f(x)dx –подынтегральным выражением, переменную x – переменной интегрирования, слагаемое C -постоянной интегрирования. , где функциюf(x) называетсяподынтегральной функцией, а выражение f(x)dx –подынтегральным выражением, переменную x – переменной интегрирования, слагаемое C -постоянной интегрирования.
(Символ 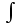 введен Лейбницем в 1675 г. Этот знак является изменением латинской буквы S. Само слово «интеграл» придумано Бернулли в 1690 г. Оно происходит от латинского integro, которое переводится, как приводить в прежнее состояние, восстанавливать. введен Лейбницем в 1675 г. Этот знак является изменением латинской буквы S. Само слово «интеграл» придумано Бернулли в 1690 г. Оно происходит от латинского integro, которое переводится, как приводить в прежнее состояние, восстанавливать.
Таблица простейших интегралов.
 Заполнить таблицу: Заполнить таблицу:
|
Презентация
Виленкин Н.Я.и др. Алгебра для 10класса. – М.: Просвещение, 1996.
Колмогоров А.Н. и др. Алгебра и начала анализа. 10-11 класс. – М.: Просвещени
Презентация
электронная презентация, выполненная в программе Power Point
|
Сабақтың ортасы
Середина урока
|
4. Оқылған материалды меңгеру
4. Освоение изученного материала
Пример. Проверьте, что функция 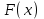 является первообраз ной для функции является первообраз ной для функции 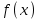 . .
Дано: F(x) = 3x4
Док-ть: f(x) = 12x3при x∈ (-∞;+∞)
Док-во: Найдем производную F(x): F'(x) = (3x4)' = 12x3 = f(x), F'(x) = f(x), значит, F(x) = 3x4первообразная для f(x) = 12x3.
 Задания на формирование умения доказывать, что функция Задания на формирование умения доказывать, что функция 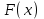 является первообразной для функции является первообразной для функции 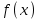 на заданном промежутке – парная работа на заданном промежутке – парная работа
1) 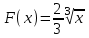 , , 
2) 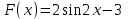 , , 
3) 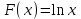 , , 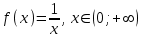
|
|
5. Оқылған материалды бекіту
5. Закрепление изученного материала.
Работа с учебником – работа в группах.
Выполним задание.
На этапе закрепления изученного материала предлагается игра «Найди свою половинку». Всем присутствующим предлагается разбиться на восемь подгрупп. Каждой подгруппе раздается карточка, на которой написано либо «функция» либо «первообразная» и соответствующее задание.
Если на вашей карточке написано слово «функция», то вы должны используя таблицу простейших интегралов найти интеграл от этой функции.
Если написано «первообразная», то вы должны найти саму функцию, используя операцию дифференцирования.
Свою «половинку» найти на доске. После чего прикрепить магнитом свой ответ. После полного набора, убедимся, что все совпадения правильные. Каким образом? Перевернуть ответы обратной стороной, где образуется ключевое слово «Интеграл» - тема занятия ( см. Приложение).
|
|
Сабақтың аяқталуы
Завершение урока
3 мин.
|
6. Үй тапсырмасы
6. Домашнее задание.
а) Конспект.
48 Первообразная, выучить наизусть определение первообразной, решить всем № 48.1(а) -48.17, решить по выбору 48.18.
|
Конспект.
Презентация
|
7. Сабақты қорытындылау және рефлексия
7. Подведение итогов занятия и рефлексия.
Домашнее задание:
Изготовление справочного материала «Первообразная и интеграл».
Опиши эмоции в конце урока
11.Рефлексия.
Какая была цель нашего урока?
|
|
Функция
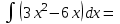
|
Первообразная

|

|
Функция
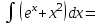
|
Первообразная

|

|
Функция
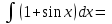
|
Первообразная
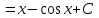
|

|
Функция
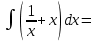
|
Первообразная
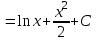
|

|
Функция

|
Первообразная
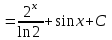
|

|
Функция
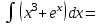
|
Первообразная
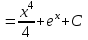
|

|
Функция

|
Первообразная

|

|
Функция
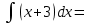
|
Первообразная
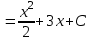
|

|

Р абота на карточками абота на карточками
Найти общий вид первообразной:
а) f (х) = 4х + 1
б) f (х) = 3х2 + 2х - 1
в) f (х) = 2 cosx – 3 sinx
г) f (х) =  - 5х3 - 7х + 5 - 5х3 - 7х + 5
|
Найти общий вид первообразной:
а) f (х) = 4х5 + 2х2 + 3
б) f (х) = х2+ 3х + 2
в) f (х) = sinx – 2 cosx
г) f (х) = 8х3 - 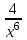
|
Вычислить интеграл
а) ∫ sinxdx
б)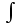 dx / х3 dx / х3
в) 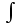 (х2+ 2х + 1) dx (х2+ 2х + 1) dx
г) 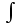 (х2+ 3) dx (х2+ 3) dx
д) 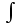 cosxdx cosxdx
|
Вычислить интеграл
а) 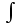 dx / sin2x dx / sin2x
б)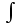 dx / х4 dx / х4
в) 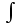 (2х + х3) dx (2х + х3) dx
г) 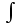 dx / соs²x dx / соs²x
д) 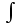 (х2+ 2) dx (х2+ 2) dx
| |
|
|
 Скачать 225.13 Kb.
Скачать 225.13 Kb.
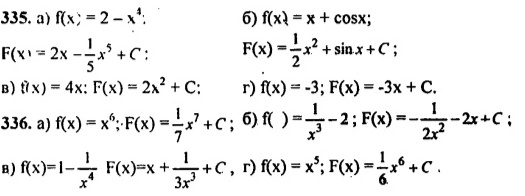 абота на карточками
абота на карточками
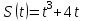 , найти его мгновенную скорость в любой момент времени.
, найти его мгновенную скорость в любой момент времени. 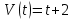 , найти закон его движения.
, найти закон его движения. .
.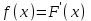 .
. 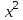 - возведение в квадрат.
- возведение в квадрат.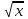 - извлечение из квадратного корня.
- извлечение из квадратного корня.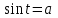 - синус угла.
- синус угла. - арксинус угла.
- арксинус угла. X выполняется равенство
X выполняется равенство 
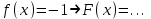
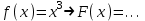

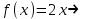
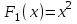 , проверка:
, проверка: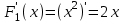
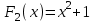 , проверка:
, проверка: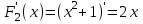
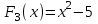 , проверка:
, проверка:
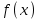 получаются друг из друга параллельным переносом вдоль оси Oy.
получаются друг из друга параллельным переносом вдоль оси Oy.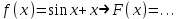

 ), то функция
), то функция 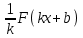 - первообразная для f(kx+b).
- первообразная для f(kx+b).
 , где функциюf(x) называетсяподынтегральной функцией, а выражение f(x)dx –подынтегральным выражением, переменную x – переменной интегрирования, слагаемое C -постоянной интегрирования.
, где функциюf(x) называетсяподынтегральной функцией, а выражение f(x)dx –подынтегральным выражением, переменную x – переменной интегрирования, слагаемое C -постоянной интегрирования.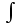 введен Лейбницем в 1675 г. Этот знак является изменением латинской буквы S. Само слово «интеграл» придумано Бернулли в 1690 г. Оно происходит от латинского integro, которое переводится, как приводить в прежнее состояние, восстанавливать.
введен Лейбницем в 1675 г. Этот знак является изменением латинской буквы S. Само слово «интеграл» придумано Бернулли в 1690 г. Оно происходит от латинского integro, которое переводится, как приводить в прежнее состояние, восстанавливать. 
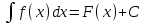
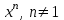


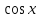
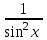
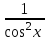
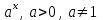
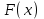 является первообраз ной для функции
является первообраз ной для функции 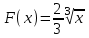 ,
, 
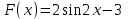 ,
, 
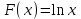 ,
, 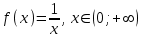
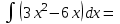


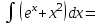





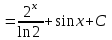

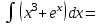
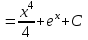




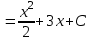

 - 5х3 - 7х + 5
- 5х3 - 7х + 5