Статистика Сущность корреляционного метода. Реферат. План Введение Сущность корреляционного метода Способы изучения корреляционных взаимосвязей
 Скачать 91.88 Kb. Скачать 91.88 Kb.
|
|
Москва 2020 План Введение Сущность корреляционного метода Способы изучения корреляционных взаимосвязей Корреляционный анализ как инструмент экономических и статистических исследований Заключение Источники 1.Введение Исследуя природу, общество, экономику, необходимо считаться со взаимосвязью наблюдаемых процессов и явлений. При этом полнота описания так или иначе определяется количественными характеристиками причинно-следственных связей между ними. Оценка наиболее существенных из них, а также воздействия одних факторов на другие является одной из основных задач статистики. Корреляционный анализ используется в экономике, социологии и психологии, медицине, управления качеством, биометрии и других сферах. Популярность корреляционного анализа объясняется тем, что коэффициенты корреляции относительно просты в расчете, и их применение не требует специальной математической подготовки. С другой стороны – коэффициенты корреляции легко интерпретировать. Однако корреляционный анализ имеет свою специфику и методику. Очень важно использование этого метода только при соблюдении предпосылок расчета того, или иного, коэффициента корреляции. Методика корреляционного анализа предполагает, не просто расчет коэффициентов корреляции, но и обязательную проверку их значимости, в основе которой лежит принцип проверки статистических гипотез, построение интервальных оценок коэффициентов корреляции. Задачи корреляционного анализа сводятся к выделению важнейших факторов, которые влияют на результативный признак, измерению тесноты связи между факторами, выявлению неизвестных причин связей и оценке факторов, оказывающих максимальное влияние на результат. 2.Сущность корреляционного метода Формы проявления взаимосвязей в экономике весьма разнообразны. В качестве двух самых общих их видов выделяют функциональную (полную) и корреляционную (неполную) связи. В первом случае величине факторного признака строго соответствует одно или несколько значений функции. Достаточно часто функциональная связь проявляется в физике, химии. В экономике примером может служить прямо пропорциональная зависимость между производительностью труда и увеличением производства продукции. Корреляционная связь (которую также называют неполной, или статистической) проявляется в среднем, для массовых наблюдений, когда заданным значениям зависимой переменной соответствует некоторый ряд вероятных значений независимой переменной. Объяснение тому - сложность взаимосвязей между анализируемыми факторами, на взаимодействие которых влияют неучтенные случайные величины. Поэтому связь между признаками проявляется лишь в среднем, в массе случаев. При корреляционной связи каждому значению аргумента соответствуют случайно распределенные в некотором интервале значения функции. Например, некоторое увеличение аргумента повлечет за собой лишь среднее увеличение или уменьшение (в зависимости от направленности) функции, тогда как конкретные значения у отдельных единиц наблюдения будут отличаться от среднего. Такие зависимости встречаются повсеместно. Например, в сельском хозяйстве это может быть связь между урожайностью и количеством внесенных удобрений. Очевидно, что последние участвуют в формировании урожая. Но для каждого конкретного поля, участка одно и то же количество внесенных удобрений вызовет разный прирост урожайности, так как во взаимодействии находится еще целый ряд факторов (погода, состояние почвы и др.), которые и формируют конечный результат. Однако в среднем такая связь наблюдается - увеличение массы внесенных удобрений ведет к росту урожайности. По направлению связи бывают прямыми, когда зависимая переменная растет с увеличением факторного признака, и обратными, при которых рост последнего сопровождается уменьшением функции. Такие связи также можно назвать соответственно положительными и отрицательными. Относительно своей аналитической формы связи бывают линейными и нелинейными. В первом случае между признаками в среднем проявляются линейные соотношения. Нелинейная взаимосвязь выражается нелинейной функцией, а переменные связаны между собой в среднем нелинейно. Существует еще одна достаточно важная характеристика связей с точки зрения взаимодействующих факторов. Если характеризуется связь двух признаков, то ее принято называть парной. Если изучаются более чем две переменные - множественной. Указанные выше классификационные признаки наиболее часто встречаются в статистическом анализе. Но кроме перечисленных различают также непосредственные, косвенные и ложные связи. Собственно, суть каждой из них очевидна из названия. В первом случае факторы взаимодействуют между собой непосредственно. Для косвенной связи характерно участие какой-то третьей переменной, которая опосредует связь между изучаемыми признаками. Ложная связь - это связь, установленная формально и, как правило, подтвержденная только количественными оценками. Она не имеет под собой качественной основы или же бессмысленна. По силе различаются слабые и сильные связи. Эта формальная характеристика выражается конкретными величинами и рассматривается в соответствии с общепринятыми критериями силы связи для конкретных показателей. В наиболее общем виде задача статистики в области изучения взаимосвязей состоит в количественной оценке их наличия и направления, а также характеристике силы и формы влияния одних факторов на другие. Для ее решения применяются две группы методов, одна из которых включает в себя методы корреляционного анализа, а другая - регрессионный анализ. В то же время ряд исследователей объединяет эти методы в корреляционно-регрессионный анализ, что имеет под собой некоторые основания: наличие целого ряда общих вычислительных процедур, взаимодополнения при рассмотрении результатов и др. Корреляционный анализ, разработанный К. Пирсоном и Дж. Юлом, является одним из методов статистического анализа взаимозависимости нескольких признаков. Основными задачами корреляционного анализа являются определение наличия связи между отобранными признаками, установление ее направления и количественная оценка тесноты связи. Задачи корреляционного анализа сводятся к измерению тесноты известной связи между варьирующимися признаками, определению неизвестных причинных связей и оценке факторов, оказывающих наибольшее влияние на результативный признак.Задачами регрессионного анализа являются выбор типа модели (формы связи), установление степени влияния независимых переменных на зависимую и определение расчетных значений зависимой переменной (функции регрессии).Термин «регрессия» (лат. «regression» -- отступление, возврат к чему-то) введен английским психологом и антропологом Ф. Гальтоном. Так как корреляционный и регрессионный анализ логически связаны и достаточно часто сначала определяют значимые факторы для анализируемого уровня конкретного риска, а потом выявляют меру их взаимосвязи с помощью уравнений регрессии, то часто в литературе и на практике говорят о корреляционно-регрессионном анализе. Поэтому потоки информации для корреляционно-регрессионного анализа должны отвечать определенным требованиям: 1.Совокупность данных (число единиц и/или наблюдений) должна быть достаточно большой по объему, чтобы в силу закона больших чисел (ЗБЧ) статистические характеристики, определяемые в процессе КРА, были достаточно типичными и надежными; 2.Качественная однородность анализируемых показателей, что предполагает близость условий формирования результативных и факторных признаков; 3.Определение необходимости анализа «выбросов», т.е. единиц наблюдений, которые по своим характеристикам существенно отличаются от основной массы данных. Одни исследователи исключают из анализа случаи с «выбросами», потому что они по определению не относятся к изучаемой популяции, другие аналитики после удаления «выбросов» исследуют их отдельно, потому что во многих случаях они представляют больший интерес, чем вся остальная выборка. Достаточно часто, удалив эти случаи из процесса анализа, мы можем потерять потенциально важную информацию о переменных или о процессах, происходящих в каждой отдельной институциональной единице финансового сектора или в секторе/подсекторе/экономике в целом. Вместо того, чтобы удалять «выбросы», можно использовать процедуры оценки параметров распределения, нечувствительных к структуре данных. Такие процедуры и модели называются робастными 4.Наблюдения или ряд исходных данных (Y, х1, х2,... xk) должны состоять из статистически независимых показателей, т.е. они не должны быть взаимосвязанными; 5.Переменные (х1, х2,... xk) должны быть линейно независимыми, т.е. корреляционная зависимость между ними не должна превышать какое-то определенное значение; 6.Каждому значению факторного признака (х) должно соответствовать нормальное распределение результативного признака (Y) с одинаковой дисперсией. Исследование связей в условиях массового наблюдения и действия случайных факторов осуществляется, как правило, с помощью экономико - статистических моделей. Выражение модели в виде функциональных уравнений используют для расчета средних значений моделируемого показателя по набору заданных величин и для выявления степени влияния на него отдельных факторов. По количеству включаемых факторов модели могут быть однофакторными и многофакторными. В зависимости от познавательной цели статистические модели подразделяются на структурные, динамические и модели связи. Необходимые условия применения корреляционного анализа. 1. Наличие достаточно большого количества наблюдений о величине исследуемых факторных и результативных показателей (в динамике или за текущий год по совокупности однородных объектов). 2. Исследуемые факторы должны иметь количественное измерение и отражение в тех или иных источниках информации. Применение корреляционного анализа позволяет решить следующие задачи: 1) определить изменение результативного показателя под воздействием одного или нескольких факторов, т.е. определить, на сколько единиц изменяется величина результативного показателя при изменении факторного на единицу; 2) установить относительную степень зависимости результативного показателя от каждого фактора. Корреляционный метод анализа взаимосвязи экономических явлений проводят в три этапа. На первом этапе осуществляется выбор формы связи между факторным и результативным признаками, т.е. выбирается тип аналитической функции. На втором этапе аналитическое уравнение связи решается путем нахождения его параметров. На третьем этапе определяется теснота связи между изучаемыми экономическими явлениями. Прежде чем подробно остановиться на каждом из трех этапов корреляционного анализа, обратим внимание на следующее. В том случае, когда определяется влияние одного фактора на результативный признак, строится однофакторная регрессионная модель (парное уравнение корреляции); когда определяется влияние двух и более факторов на результативный признак, строится многофакторная регрессионная модель (уравнение множественной корреляции). При подборе факторов для регрессионной модели следует помнить, что факторы не должны находиться в функциональной связи с результативным признаком. В противном случае должен применяться индексный метод анализа, а не корреляционный. Следует также знать, что число наблюдений для построения однофакторной регрессионной модели должно быть не менее 10 - 12. Первый этап корреляционного анализа Для определения формы связи между факторным и результативным признаками, т.е. для установления типа аналитической функции связи применяют различные статистические методы. Так, характер и направление связи между изучаемыми явлениями можно установить, применяя метод статистических группировок. С помощью данного метода наличие связи между явлениями устанавливается визуально. Для выявления тенденции изменения результативного признака при изменении факторного могут использоваться такие статистические методы, как метод укрупнения интервалов, метод скользящей средней, метод аналитического выравнивания. Чаще всего для установления формы зависимости между факторным и результативным признаками применяют графический метод. При прямолинейной форме зависимости между факторным и результативным признаками функция связи имеет вид прямой: На втором этапе корреляционного анализа решают аналитическое уравнение связи путем нахождения его параметров а0, а1,…, аn. Параметр а0 означает влияние на результативный признак не включенных в регрессионную модель факторов. Как правило, экономической интерпретации параметр а0 не подлежит. Параметры а1,.., аn (коэффициенты регрессии) означают величину результативного признака при изменении факторного признака на единицу измерения. В случае прямолинейной формы зависимости параметры аналитического уравнения связи находятся путем решения следующей системы уравнений: 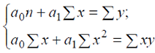 В случае параболической формы зависимости параметры аналитического уравнения связи находятся путем решения следующей системы уравнений: 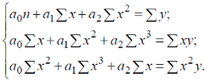 В случае гиперболической формы зависимости параметры аналитического уравнения связи находятся путем решения следующей системы уравнений: 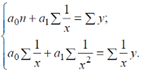 Для экономической интерпретации аналитического уравнения связи можно воспользоваться также коэффициентом эластичности, который рассчитывается по формуле: Коэффициент эластичности показывает, на сколько процентов в среднем изменяется результативный признак при изменении факторного на 1%. На третьем этапе корреляционного анализа проводят оценку тесноты связи между факторным и результативным признаками с помощью показателей тесноты связи. В случае линейной связи между факторным и результативным признаками производят расчеты линейного коэффициента корреляции по следующей формуле: Где: Линейный коэффициент корреляции варьирует в пределах от -1 до +1. Положительное его значение говорит о прямой связи, отрицательное - об обратной. Близость к нулю говорит о слабой связи, близость к ±1 говорит о существенной связи, при r = ± 1 - связь функциональная. Интерпретация коэффициентов корреляции
Для экономической интерпретации линейного коэффициента корреляции применяется коэффициент детерминации. Он определяется по формуле: Коэффициент детерминации характеризует долю дисперсии результативного признака, объясняемую влиянием соответствующего факторного признака. В случае криволинейной зависимости (параболической, гиперболической) тесноту связи между факторным и результативным признаками определяют с помощью корреляционного отношения по формуле: 3.Способы изучения корреляционных взаимосвязей Корреляционная (стохастическая) связь – это неполная, вероятностная зависимость между показателями, которая проявляется только в массе наблюдений. Различают парную и множественную корреляцию. Парная корреляция – это связь между двумя показателями, один из которых является факторным, а другой результативным. Множественная корреляция возникает от взаимодействия нескольких факторов с результативным показателем. Для изучения стохастических соотношений используются следующие способы экономического анализа: сравнение параллельных и динамических рядов, аналитические группировки, графики. Однако они позволяют выявить только общий характер и направление связи. Для определения степени влияния каждого фактора на уровень результативного показателя применяются способы корреляционного, дисперсионного, компонентного, современного многомерного факторного анализа и т. д. Наиболее широкое применение в экономических исследованиях нашли приемы корреляционного и регрессионного анализа, которые позволяют количественно выразить взаимосвязь между показателями.Регрессионный анализ предназначен для выбора формы связей, типа модели, определения расчетных значений зависимой переменной (результирующего признака). Применение корреляционного анализа позволяет решить следующие задачи: 1. Определить изменение результативного показателя под воздействием одного или нескольких факторов (в абсолютном измерении), т. е. выяснить, на сколько единиц изменяется величина результативного показателя при изменении факторного на единицу. 2. Установить относительную степень зависимости результативного показателя от каждого фактора. Необходимые условия применения корреляционного анализа: 1. Наличие достаточно большого количества наблюдений о величине исследуемых факторных и результативных показателей (в динамике или за текущий год по совокупности однородных объектов). 2. Исследуемые факторы должны иметь количественное измерение и отражение в тех или иных источниках информации. При использовании способов парной корреляции связь между корреляционным фактором и результативным показателем характеризуется прежде всего коэффициентом корреляции, который может изменяться от нуля до единицы. Чем ближе он к единице, тем более тесная связь между анализируемыми показателями. Коэффициент корреляции с плюсом указывает на прямую связь, с минусом – на обратную: Где р – число наблюдений; у – результативный показатель; х – факторный показатель. Далее корреляционый анализ дополняется регрессионным анализом. Зависимость исследуемого показателя от одного фактора в простейшем виде можно представить формулой у = а + bх. Для определения параметров (а и b) этого уравнения используется метод наименьших квадратов, решается такая система уравнений: Размер влияния фактора на результат оценивается по параметру b (коэффициент регрессии), что показывает, на сколько единиц изменяется хозяйственный результат при изменении размера фактора на единицу. При измерении тесноты связи при криволинейной зависимости используется универсальное корреляционное отношение: 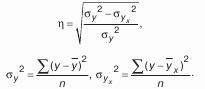 Множественный корреляционный анализ более сложен, он состоит из нескольких этапов: 1. Определение наиболее существенных факторов. 2. Сбор и оценка исходной информации. 3. Изучение характера и моделирование связи между факторами и результативным показателем (подбор математического уравнения, наиболее точно выражающего сущность связи). 4. Расчет показателей связи. 5. Статистическая оценка результатов корреляционного анализа. 4. Корреляционный анализ как инструмент экономических и статистических исследований. Корреляционный анализ представляет собой множество математически обоснованных методов, с помощью которых происходит обнаружение корреляционной зависимости между парой факторов или признаков, имеющих случайную составляющую. В наборе приемов, используемых в данном методе исследования, широкое распространение получили: - построение корреляционных полей, составление корреляционных таблиц; - расчёт корреляционного отношения или выборочных коэффициентов; - проверка гипотезы статистических значимостей связей. Продолжение исследований приводит к установлению конкретных видов взаимосвязи между величинами. Взаимосвязь между случайными признаками или факторами, количество которых превышает три, нуждается в использовании метода многомерного анализа. Поле и таблица, построением которых занимается корреляционный анализ, используются в качестве вспомогательных средств в ходе анализа выборочных данных. Нанося на поле координатной плоскости выборочные точки, приходят к получению так называемого корреляционного поля. По тому, как расположились точки, уже можно составить предварительный прогноз и определить форму зависимости случайных величин. Численная обработка результатов требует группировки их в виде корреляционной таблицы. Впервые появившись в XVIII веке, термин «корреляция» с лёгкой руки палеонтолога Жоржа Кювье начал активно использоваться для процесса восстановления облика ископаемых животных по некоторым частям его останков. Развитие узконаправленного палеонтологического метода привело к тому, что корреляционный анализ начали использовать в самых различных сферах человеческой жизнедеятельности. Этот метод является привлекательным для обработки статистических данных. Корреляционный анализ в статистике впервые использовал английский биолог и статистик Фрэнсис Гальтон в конце XIX века. В дальнейшем развитие метода позволило измерять тесноту связи между парой и большим количеством переменных. Корреляционный анализ имеет тесную связь с регрессионным анализом. Особое место занимает корреляционный анализ в экономике. Но его использование накладывает ряд ограничений. Прежде всего, это наличие достаточного количества измерений и данных для изучения. Практика подсказывает, что количество наблюдений должно превышать в 5-6 раз число факторов. Оптимальным вариантом является наличие числа наблюдений, превышающего количество факторов в несколько десятков раз. В таком случае действует закон больших чисел, благодаря ему произойдёт взаимопогашение случайных колебаний. Также следует добиться того, чтобы весь набор факторных и результативных признаков подчинился нормальному многомерному распределению. Бывают случаи, когда объёма совокупности недостаточно для осуществления формального тестирования на соответствие нормальности распределения, тогда определения закона распределения визуально осуществляется по данным корреляционного поля. Если точки расположились согласно линейной тенденции, то вполне реально сделать вывод, что набор исходных данных удовлетворят требованиям нормального закона распределения. В исходной совокупности значений необходимо следить за качественной однородностью. Наличие факта корреляционной зависимости ещё не даёт основания для утверждения, что произвольно взятая переменная предшествует появлению второй или служит причиной её изменений, другими словами, между ними нет строгой причинной связи между собой, и даже возможно действие какого-нибудь третьего фактора. Применяя на практике результаты анализа на основе корреляционных методов исследования, можно сделать ряд определённых выводов о наличии, а самое главное, о характере взаимозависимости. Это уже даёт весомую долю информации об объекте, находящемся под исследованием. 5.Заключение В заключении хотелось бы отметить, что корреляционный метод является важнейшим методом изучения взаимосвязей экономических явлений. Использование в научных исследованиях метода корреляционного анализа позволяет определить связь между различными факторами и результативными показателями. При этом необходимо учитывать, что высокий коэффициент корреляции можно получить и из абсурдной пары или множества данных, в связи с чем данный вид анализа нужно осуществлять на достаточно большом массиве данных. Благодаря корреляционному анализу является возможность глубже исследовать взаимосвязи экономических явлений и процессов, выявить влияние факторов на результаты хозяйственной деятельности, выявить и подсчитать резервы повышения эффективности производства. Все это положительно сказывается на осуществлении управленческой, маркетинговой и других видов деятельности, принятии экономически обоснованных хозяйственных решений. Таким образом, корреляционный анализ имеет большое значение в экономическом анализе, изучении общественных явлений и процессов. В частности, он помогает решить следующие задачи: - Установление характера и тесноты связи между изучаемыми явлениями; - Количественное измерение степени влияния отдельных факторов и их совокупности на уровень явления, которое изучается; - Расчет количественных изменений рассматриваемого явления при прогнозировании показателей и объективная оценка хозяйственной деятельности предприятия. Большое значение отводится корреляционной анализа в исследовании корреляционных связей на производстве, в том числе между уровнем производительности труда и вооруженностью ее основными средствами, между урожайностью и количеством внесенных удобрений, между себестоимостью и выпуском продукции и др. 6.Источники 1.Горемыкина Т.К. «Общая теория статистики» 2.Шмойлова Р.А. «Теория статистики» 3.Сергеева И.И. «Статистика» 4.Литвинюк А.С. «Экономический анализ» 5.Козлов А.И. «Статистика» 1.Корреляционный анализ используется в экономике, социологии и психологии, медицине, управления качеством, биометрии и других сферах. Расскажите зачем корреляционный анализ используется в экономике, социологии и психологии, медицине, управления качеством, биометрии и других сферах? На производственном предприятии, упаковывающем свои изделия в тонкую полиэтиленовую пленку перед складированием уровень дефектности в апреле существенно вырос. Были высказаны несколько гипотез, одна из которых – влияние влажности воздуха в помещении цеха. В зимний период влажность была стабильна, а с отключением центрального отопления стала зависеть от влажности на улице. Для проверки гипотезы были собраны данные за неделю:
Далее был применен корелляционный анализ: 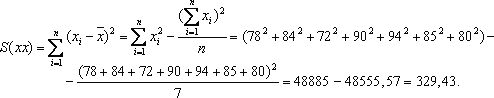 S(yy) = (2,22+2,62+2,12+2,72+2,82+2,62+2,22) - (2,2+2,6+2,1+2,7+2,8+2,6+2,2)2/7 = 42,74-42,26= 0,48. 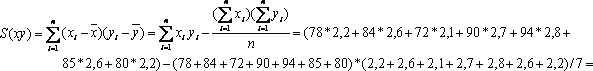 =1444,4-1432,5=11,9. Значение коэффициента корреляции показывает наличие сильной положительной связи, т.е. чем больше влажность в помещении, тем больше будет доля дефектов при упаковке в данном помещении. 2. Что такое корреляционная зависимость между уровнями различных рядов динамики? |
