план скоростей. Планы скоростей. Планы скоростей Строим планы скоростей
 Скачать 80.54 Kb. Скачать 80.54 Kb.
|
|
Планы скоростей Строим планы скоростей для 8 положений механизма. Выбираем точку pV (полюс плана скоростей); в этой точке будут располагаться все точки, скорости которых равны нулю. Из точки pVi (i = 0-7) проводим вектор скорости точки А' перпендикулярно звену ОА' в направлении его угловой скорости. Длина этого вектора равна длине отрезка [pVa'], выбранного при расчете масштабного коэффициента плана скоростей. Отмечаем на чертеже точку а'. Далее через точку а' проводим прямую, перпендикулярную звену А'В. Через точку pV проводим прямую, параллельную направляющей движения ползуна В. На пересечении этих двух линий отмечаем искомую точку b. Соединяем точки А' и В между собой. Полная скорость точки В будет определяться отрезком рb. Скорость точки S2, центра тяжести шатуна, найдется из принципа подобия плана скоростей: Из точки pVi (i = 0-7) проводим вектор скорости точки А перпендикулярно звену ОА в направлении его угловой скорости. Длина этого вектора равна длине отрезка [pVa'], выбранного при расчете масштабного коэффициента плана скоростей. Отмечаем на чертеже точку а. Далее через точку а проводим прямую, перпендикулярную звену АС. Через точку pV проводим прямую, параллельную направляющей движения ползуна С. На пересечении этих двух линий отмечаем искомую точку c. Соединяем точки a и c между собой. Полная скорость точки С будет определяться отрезком рc. Скорость точки S4, центра тяжести шатуна, найдется из принципа подобия плана скоростей: Находим действительные значения скоростей всех точек Определяем угловую скорость звеньев 2 и 4 Для определения направления угловой скорости шатуна 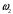 нужно перенести вектор нужно перенести вектор 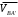 в точку В плана механизма и определить в какую сторону вектор в точку В плана механизма и определить в какую сторону вектор 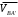 создает вращение шатуна вокруг точки А'; направление этого вращения покажет направление угловой скорости шатуна ω2. создает вращение шатуна вокруг точки А'; направление этого вращения покажет направление угловой скорости шатуна ω2.Для определения направления угловой скорости шатуна 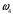 нужно перенести вектор нужно перенести вектор 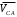 в точку С плана механизма и определить в какую сторону вектор в точку С плана механизма и определить в какую сторону вектор 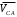 создает вращение шатуна вокруг точки А; направление этого вращения покажет направление угловой скорости шатуна ω4. создает вращение шатуна вокруг точки А; направление этого вращения покажет направление угловой скорости шатуна ω4.Для остальных положений механизма проводим аналогичное построение и результаты построений заносим в таблицы 2 и 3. Планов ускорений Построение планов ускорений ведем в следующей последовательности. Выбираем положение полюса плана ускорений, точки ра. В этой точке будут находиться все точки, ускорения которых равны нулю. Из точки ра проводим вектор нормального ускорения точки А' параллельно звену А'О, в направлении от точки А' к точке О (центру вращения) и откладываем на нём отрезок [paa], равный 50 мм. Из точки а' проводим вектор нормального ускорения точки В при её вращении вокруг точки А' ( 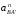 ). Этот вектор проводим параллельно звену ВА', в направлении от точки В к точке А' (центру вращения). ). Этот вектор проводим параллельно звену ВА', в направлении от точки В к точке А' (центру вращения).Используя данные табл. 4, определяем длину отрезка [a'n2]. В табл. 5 приведены значения отрезка [a'n2], отображающего ускорение 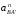 . .Далее из точки а проводим вектор нормального ускорения точки C при её вращении вокруг точки А ( 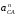 ). Этот вектор проводим параллельно звену CА, в направлении от точки C к точке А (центру вращения). ). Этот вектор проводим параллельно звену CА, в направлении от точки C к точке А (центру вращения).Используя данные табл. 4, определяем длину отрезка [an4]. В табл. 5 приведены значения отрезка [an4], отображающего ускорение 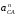 . .Через точку n2 проводим прямую, перпендикулярную звену ВА', а из точки ра – прямую (параллельно направляющей точки В). На пересечении этих прямых отмечаем искомую точку b. Полное ускорение точки В будет определяться отрезком [pab]. Ускорение точки В во вращательном движении вокруг точки A' будет определяться отрезком [bа']. Через точку n4 проводим прямую, перпендикулярную звену CА, а из точки ра – прямую (параллельно направляющей точки С). На пересечении этих прямых отмечаем искомую точку c. Полное ускорение точки C будет определяться отрезком [pac]. Ускорение точки C во вращательном движении вокруг точки A будет определяться отрезком [cа]. Ускорение точки S2, центра тяжести шатуна, найдется из принципа подобия плана ускорений: Угловые ускорения звеньев 2 и 4 Для определения направления углового ускорения шатуна 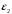 нужно перенести вектор нужно перенести вектор 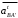 в точку В плана механизма и определить в какую сторону вектор в точку В плана механизма и определить в какую сторону вектор 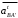 создает вращение шатуна вокруг точки А'. создает вращение шатуна вокруг точки А'.Для определения направления углового ускорения шатуна 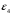 нужно перенести вектор нужно перенести вектор 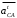 в точку С плана механизма и определить в какую сторону вектор в точку С плана механизма и определить в какую сторону вектор 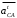 создает вращение шатуна вокруг точки А. создает вращение шатуна вокруг точки А.Плана сил 2 и 3 Для построения плана сил, действующих на группу звеньев 2 и 3, проведём на формате прямую линию параллельно A'B. На прямой линии выберем произвольно точку 0, в которую поместим начало вектора 0-1, изображающего реакцию 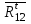 . В точку 1, т.е. конец вектора 0-1, поместим начало следующего вектора 1-2, изображающего силу . В точку 1, т.е. конец вектора 0-1, поместим начало следующего вектора 1-2, изображающего силу 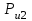 . Аналогичным образом выполним сложение векторов 3-4, 4-5, сохраняя последовательность их расположения на плане сил такой же, как и в уравнении равновесия группы. Затем через точку 6, т.е. конец вектора 5-6, изображающего силу Р3 проведём прямую линию перпендикулярно оси направляющей точки В. Точка пересечения прямых (точка 7) будет являться концом вектора 7-6, изображающего реакцию R03 и началом вектора 7-0, изображающего реакцию . Аналогичным образом выполним сложение векторов 3-4, 4-5, сохраняя последовательность их расположения на плане сил такой же, как и в уравнении равновесия группы. Затем через точку 6, т.е. конец вектора 5-6, изображающего силу Р3 проведём прямую линию перпендикулярно оси направляющей точки В. Точка пересечения прямых (точка 7) будет являться концом вектора 7-6, изображающего реакцию R03 и началом вектора 7-0, изображающего реакцию 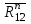 . .Из условия равновесия звена 3 следует 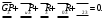 где R23 - реакция, действующая на звено 3 со стороны звена 2 и проходящая через центр шарнира B. Соединив на плане сил точки 7 и 3, получим вектор 7-3, изображающий реакцию R23. Определим реакции 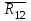 , , 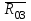 и и 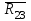 по величине: по величине:Силовой расчет начального звена Изобразим на формате схему начального звена 1, входящего в кинематическую пару со стойкой. Масштабный коэффициент построений примем μS= 0,001 м/мм. На звено 1 действуют силы: 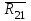 - реакция со стороны отброшенного звена 2, - реакция со стороны отброшенного звена 2, 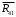 - реакция со стороны отброшенного звена 4, - реакция со стороны отброшенного звена 4, 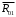 - реакция со стороны стойки, Мур - уравновешивающий момент и масса кривошипа G1. Реакция - реакция со стороны стойки, Мур - уравновешивающий момент и масса кривошипа G1. Реакция 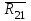 проходит через точку А'. Реакция проходит через точку А'. Реакция 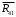 проходит через точку А. проходит через точку А.Причём 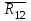 = - = -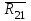 , , 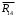 = - = -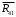 . Реакция . Реакция 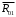 проходит через точку О. Направление и величина реакции проходит через точку О. Направление и величина реакции 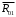 неизвестны. Направление и величина уравновешивающего момента сил Мур также подлежат определению. неизвестны. Направление и величина уравновешивающего момента сил Мур также подлежат определению.Определим уравновешивающую силу 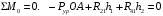 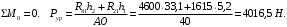 Составим векторное уравнение равновесия системы сил, действующих на звено 1. 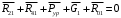 Принимаем масштабный коэффициент Р =50 Н/мм и определяем длины векторов реакций 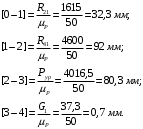 Определим реакцию 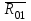 по величине: по величине: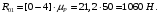 Уравновешивающий момент Мур равен 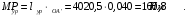 Определение уравновешивающей силы методом рычага Н.Е. Жуковского В качестве проверки определим для рассматриваемого положения механизма уравновешивающею силу с помощью рычага Жуковского. Решение задачи ведем в следующей последовательности. План скоростей для рассматриваемого рабочего положения механизма поворачиваем на 900 в сторону, противоположную вращению кривошипа. Найденные силы пар переносим на рычаг Жуковского по общему правилу. Все силы, действующие на звенья механизма, включая силы инерции и искомую уравновешивающую силу, переносим параллельно самим себе в одноименные точки повернутого плана. Если на звено действует момент сил, то этот момент следует предварительно представить на звене механизма как пару сил, вычислив их величины. Плечо пары выбирается на звене, к которому приложен момент, произвольно 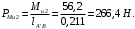 Составляем уравнение моментов всех сил относительно полюса повернутого плана скоростей: 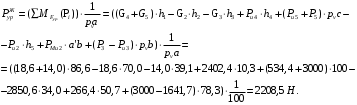 Определим величину погрешности при двух видах расчета 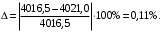 Так как расхождение результатов не превышает допустимого значения в 5%, расчеты выполнены с достаточной степенью точности. |
