Площадь трапеции
8 класс
Планируемые образовательные результаты
|
Предмет
ные
|
Метапредметные результаты (УУД)
|
Личностные
|
Регулятивные
|
Познавательные
|
Коммуникативные
|
Знать: определение понятия «Высота трапеции»
Понимать: для чего необходимо умение находить площадь трапеции
Уметь: применять формулу площади трапеции
|
1.1. принимать учебную задачу;
1.2. планировать (в сотрудничестве с учителем и одноклассниками или самостоятельно) необходимые действия, операции, действовать по плану;
1.3. контролировать процесс и результаты деятельности, вносить необходимые коррективы;
1.4. адекватно оценивать свои достижения, осознавать возникающие трудности, искать их причины и пути преодоления.
|
2.1.осознавать познавательную задачу;
2.2. читать и слушать, извлекая нужную информацию, понимать информацию, выполнять УУД;
2.3.осуществлять для решения учебных задач операции анализа, синтеза, сравнения;
2.4. устанавливать причинно-следственные связи, делать выводы.
|
3.1. вступать в учебный диалог с учителем, одноклассниками, участвовать в общей беседе, соблюдая правила речевого поведения;
3.2. задавать вопросы, слушать и отвечать на вопросы других, формулировать собственные мысли, высказывать и обосновывать свою точку зрения;
3.3. строить небольшие монологические высказывания;
3.4. осуществлять совместную деятельность в парах и рабочих группах с учётом конкретных учебно-познавательных задач.
|
4.1. положительное отношение к учению, к познавательной деятельности, желание приобретать новые знания, умения, совершенствовать имеющиеся;
4.2. осознавать свои трудности и стремиться к их преодолению;
4.3. осваивать новые виды деятельности, участвовать в творческом, созидательном процессе.
|
Организационная структура урока
Этапы урока
|
Задачи этапа
|
Деятельность учителя
|
Деятельность учащихся
|
Организационный момент
УУД: 4.1
|
Уточнение направления актуализации изученного материала. Положительный настрой на урок.
|
Приветствует учащихся, проверяет готовность учащихся к уроку.
|
Приветствуют учителя, проверяют свою готовность к уроку.
|
Вхождение в тему урока и создание условий для осознанного восприятия нового материала
УУД: 1.3, 1.4, 2.2, 3.1-3.3, 4.1, 4.2
|
Повторение и актуализация знаний. Мотивация учебной деятельности.
|
Предлагает учащимся устную работу на повторение по темам «Площадь параллелограмма», Площадь треугольника»
|
Необходимо вспомнить знания по теме «Площадь параллелограмма», Площадь треугольника», формулы вычисления площадей прямоугольника, параллелограмма, треугольника.
|
УУД: 1.1, 2.1, 2.2-2.4, 3.1-3.3, 4.1
|
Определение темы, цели и задач урока. Самоопределение в деятельности.
|
Подводит итог того, что ученики уже много знают и умеют. Подводит учащихся к формулированию цели и задач урока, предлагая выполнить задание на определение высоты трапеции, подводит к выводу формулы площади трапеции.
|
Выполняют задание на определение высоты трапеции. Выдвигают гипотезу о формуле площади трапеции. Обсуждают полученный результат.
Формулируют цель и задачи урока и план своей деятельности.
|
Организация и самоорганизация учащихся в ходе усвоения материала. Организация обратной связи.
УУД: 1.2, 1.3, 2.2-2.4, 3.1, 3.2 4.3
|
Организация деятельности учащихся по освоению учебной информации на уровне «знание».
|
Предлагает сверить свои выводы и догадки с определением в учебнике; Дает под запись в тетради доказательство теоремы о площади трапеции.
|
Самостоятельно формулируют определение высоты трапеции, проверяют себя по учебнику (стр.237)
Записывают в тетрадь доказательство теоремы о площади трапеции.
|
Релаксация
УУД: 4.3
|
Снятие напряжения, разгрузка
|
Выполняет упражнения психологической и физической разгрузки
|
Выполняют дыхательную гимнастику по технологии биологически обратной связи (БОС)
|
Практикум
УУД: 1.2, 1.3, 2.2, 2.3, 3.1-3.4, 4.1
|
Организация деятельности учащихся по освоению учебной информации на уровне «умения».
|
Предлагает решить задачи с электронной доски
|
Работают в тетрадях, записывая правильное решение и производя проверку полученного результата.
Устно объясняют выбор правильного решения задачи.
|
Проверка полученных результатов
УУД: 1.3, 1.4, 2.2, 4.2, 4.3
|
Организация деятельности учащихся по осознанию ими результата освоения учебной информации.
|
Организует работу по выполнению устной работы по вопросам учебника. (стр. 238)
|
Выполняют проверку ответов на вопросы в парах.
|
Подведение итогов.
Рефлексия.
Домашнее задание.
УУД: 1.4, 4.2.
|
Проведение самоанализа и самооценки собственной деятельности. Обеспечить понимание учащимися цели, содержания и способов выполнения домашнего задания.
|
Организовывает подведение итогов. Даёт качественную оценку работы класса и отдельных учащихся. Записывает домашнее задание:
|
Повторяют, что узнали, какие умения и навыки отрабатывали и закрепляли.
Анализируют качество собственной работы на уроке, отвечая на вопрос: «Что нового я узнал?»
Осознают продвижение в своём умственном развитии, отвечая на вопрос: «Чему научился на уроке?»
|
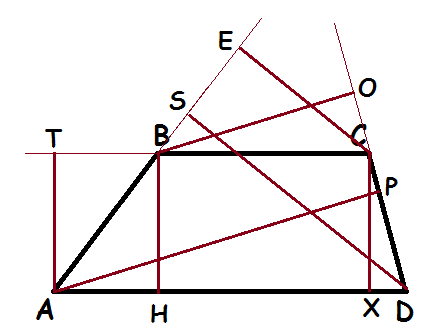
Ход урока:
Дана трапеция АВСD, для которой выполнены дополнительные построения.
Что за отрезки проведены?
Разбейте отрезки на группы.
Сформулируйте признак разбиения.
Учитель подводит к определению высоты трапеции.
Составляет с учащимися схему определения понятия. (слайд 4)
В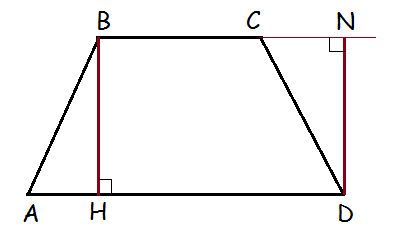 ысота трапеции – 1) отрезок, 2) проведен из любой вершины на противолежащее основание или его продолжение, 3) перпендикулярен противолежащему основанию. ысота трапеции – 1) отрезок, 2) проведен из любой вершины на противолежащее основание или его продолжение, 3) перпендикулярен противолежащему основанию.
BH, DN – высоты, BH=DN.
Далее повторим формулы площадей. К данным многоугольникам подберите формулы для вычисления их площади: (соединить стрелками). Вспомните свойства площадей. – Свойство 1. Равные многоугольники имеют равные площади. – Свойство 2. Если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников.
И сейчас вы в группах проведете небольшое исследование по выводу формулы площади трапеции. На листе начертите трапеции и выполните задание, согласно инструкции. (Каждой группе дается лист А4, где они должны совместной работой начертить трапецию, разбить ее на известные многоугольники, формулы площадей которые они знают и, используя свойство площадей, вывести формулу площади трапеции) Варианты решения: 1. 2. 3. 4. 5. 6. S трапеции=S треугольника +S прямоугольника +S треугольника. S трапеции=S большого треугольника – S маленького треугольника. S трапеции=S параллелограмма – S треугольника. S трапеции=S прямоугольника – S треугольника –S треугольника. S трапеции=S треугольника +S треугольника.
Мы знаем, как найти площадь квадрата, прямоугольника, треугольника, параллелограмма и ромба.
Рассмотрим ещё один многоугольник – трапецию.
(Работа в группах)
Каждая группа получает задание, найти площадь трапеции.
Проблемная ситуация:
Для всех групп:
Большее основание трапеции b
Меньшее основание трапеции а
Высота трапеции h.
ЗАДАЧА1(первая группа)
Найдите площадь трапеции, разбив её площадь на 2 треугольника и прямоугольник, как показано на рисунке. (Трапеция не равнобокая.)

Sтрап= S1+S2+S3
Sтрап=½h(b-a)+ah=h½(a + b)
ЗАДАЧА2(вторая группа)
Найдите площадь трапеции, разбив её на треугольник и параллелограмм, как показано на рисунке.

Sтрап.= S1+S2 =ah +½(b – a)h = h½(a + b)
ЗАДАЧА3(третья группа)
Найдите площадь трапеции

Sтрап.=½ ha + ½hb= h½(a + b)
Группы делают вывод, что для того, чтобы найти площадь трапеции надо полусумму её оснований умножить на высоту.
Формулу нахождения площади трапеции записывают в тетрадь.
 S =½(a + b)h S =½(a + b)h
5) Этап первичного закрепления новых знаний.
Рабочая тетрадь №42; №43
II. Этап проверки домашнего задания. (2 мин.)
1. Что мы с вами изучали на предыдущих уроках? (Изучали формулы площадей квадрата, прямоугольника, параллелограмма, ромба, треугольника.)
2. Что понимают под площадью многоугольника? (Площадь – это величина той части плоскости, которую занимает данный многоугольник.)
3. Чем выражается площадь? (Площадь выражается положительным числом. Это число показывает, сколько раз единица измерения укладывается в данном многоугольнике.)
4. Что принято за единицу площади? (За единицу измерения площади принимают площадь квадрата со стороной, равной единице длины.)
5. Какие единицы измерения площадей вы знаете? (1мм2, 1см2, 1дм2, 1м2, 1км2; 1 а, 1 га – в сельском хозяйстве; 1 барн = 10-28м2– в химии и физике.)
6. Какие старинные русские единицы площади вы знаете? (1 кв.верста, 1 десятина, 1 кв.сажень.)
7. Назовите свойства площадей.
– Свойство 1. Равные многоугольники имеют равные площади.
– Свойство 2. Если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников.
– Свойство 3. Площадь квадрата равна квадрату его стороны.
8. Как можно найти площадь произвольной геометрической фигуры?
Конспект урока "Площадь трапеции"
Асадуллина Зиля Мазитовна, учитель математики
Разделы: Математика
“ …Всё в природе подлежит измерению,
всё может быть сосчитано”
Лобачевский Н. И.
Дидактическая цель урока: создать условия для осознания и осмысления блока новой учебной информации средствами технологии проблемного обучения и с использованием элементов личностно-ориентированного обучения.
Цели урока:
образовательные: продолжить формировать навыки выведения формул для вычисления площади многоугольников на примере трапеции, закрепить навыки решения задач по выведенной формуле;
развивающие: развитие воображения, мыслительных процессов анализа, сравнения, обобщения;
воспитательные: формирование коммуникативных умений.
Номер урока: первый.
Тип урока: урок изучения нового материала и первичного закрепления новых знаний.
Технологии обучения: личностно– ориентированная, технология сотрудничества.
Формы организации учебной деятельности: индивидуальная, фронтальная, работа в группах.
Методы обучения: репродуктивный, частично-поисковый.
Оборудование: компьютер, проектор, экран, раздаточный материал – треугольники, четырехугольники, трапеции, презентация.
Этапы урока:
Организационный этап.
Этап проверки домашнего задания.
Этап подготовки учащихся к активному сознательному усвоению материала.
Этап усвоения новых знаний.
Первичная проверка усвоения знаний.
Физкультминутка.
Этап первичного закрепления знаний.
Подведение итогов урока. .Рефлексия.
Этап информации учащихся о домашнем задании.
Ход урока
1. Организационный момент. (1 мин.)
До начала урока учащиеся разбиваются на группы по 4 человека, выбирается в каждой группе ведущий (организует работу группы, осуществляет связь группы с учителем, фиксирует предложенные членами групп варианты ответов и оформляет результаты работы группы).
– Ребята, восточная мудрость гласит: “Можно коня привести к воде, но нельзя заставить его пить”. И человека невозможно заставить учиться хорошо, если он не старается узнать больше, нет желания работать над своим развитием. Ведь знания только тогда знания, когда они приобретены усилиями своей мысли, а не одной памятью. Сегодня у нас поисково – исследовательская работа. Мы с вами вспомним все, что изучили о площадях. И постараемся сделать открытие новой формулы. Ведь мы сегодня с вами кто? Правильно! Исследователи!
II. Этап проверки домашнего задания. (2 мин.)
1. Что мы с вами изучали на предыдущих уроках? (Изучали формулы площадей квадрата, прямоугольника, параллелограмма, ромба, треугольника.)
2. Что понимают под площадью многоугольника? (Площадь – это величина той части плоскости, которую занимает данный многоугольник.)
3. Чем выражается площадь? (Площадь выражается положительным числом. Это число показывает, сколько раз единица измерения укладывается в данном многоугольнике.)
4. Что принято за единицу площади? (За единицу измерения площади принимают площадь квадрата со стороной, равной единице длины.)
5. Какие единицы измерения площадей вы знаете? (1мм2, 1см2 , 1дм2, 1м2, 1км2; 1 а, 1 га – в сельском хозяйстве; 1 барн = 10-28м2 – в химии и физике.)
6. Какие старинные русские единицы площади вы знаете? (1 кв.верста, 1 десятина, 1 кв.сажень.)
7. Назовите свойства площадей.
– Свойство 1. Равные многоугольники имеют равные площади.
– Свойство 2. Если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников.
– Свойство 3. Площадь квадрата равна квадрату его стороны.
8. Как можно найти площадь произвольной геометрической фигуры? (При помощи палетки, но это не совсем удобный способ, да и не точныйю)
– Палетка (от франц. palette – пластинка, планка), начерченная на прозрачной бумаге, стекле или целлулоидной пластинке сетка линий, образующих квадраты известных размеров, при помощи которых определяется площадь участков на плане или карте.
9. Площади каких геометрических фигур мы умеем находить? Как? (площадь квадрата, прямоугольника, треугольника, параллелограмма, ромба.)
10. Для чего нужно знать и уметь находить площади фигур? Где это применяется на практике? (В строительстве, в сельском хозяйстве.)
– Когда начали применять площади и для каких целей?
1) Тест по проверке теоретического материала.
1. Выберите верные утверждения:
а) площадь прямоугольника равна произведению двух его сторон;
б) площадь квадрата равна квадрату его стороны;
в) площадь прямоугольника равна удвоенному произведению двух его соседних сторон.
2. Закончите фразу: площадь ромба равна половине произведения…
а) его сторон;
б) его стороны и высоты, проведенной к этой стороне;
в) его диагоналей.
3. По формуле S= a∙hаможно вычислить площадь:
а) параллелограмма;
б) треугольника;
в) прямоугольника.
4. Выберите верное утверждение. Площадь прямоугольного треугольника равна:
а) половине произведения его стороны на какую-либо высоту;
б) половине произведения его катетов;
в) произведению его стороны на проведенную к ней высоту.
5. Площадь треугольника по известным трем сторонам можно вычислить с помощью:
а) теоремы Пифагора;
б) теоремы Фалеса;
в) формулы Герона.
– А теперь поменяйтесь тетрадями с соседом и выполните проверку. За каждое правильно выполненное задание 1 балл.
(Ответы высвечиваются на экране.)
Ответы: 1) а, б; 2) в; 3) а; 4)б; 5) в.
2) Огород имеет форму трапеции, основания которой 12 и 18 м, а расстояние между основаниями 6 м. Сколько (по весу) семян требуется, чтобы засадить его капустой, если на каждый кв м их потребуется 0,5 г. 3) Для остекления уличного шестиугольного фонаря требуется 6 одинаковых кусков стекла в виде трапеции, у которых основания 200, 120 мм, высота 400 мм. Сколько кв м стекла требуется для 100 таких фонарей?
Этапы урока, целевые ориентиры, время
|
Задания, выполнение которых учащимися приведет к достижению запланированных результатов
|
Деятельность учителя
|
Деятельность учащихся и возможные варианты ответов
|
Планируемые результаты, формирование УУД
|
Задания базового уровня
|
Задания повышенного уровня
|
предметные
|
личностные,
метапредметные
|
I.
Самоопределение к учебной деятельности
Цель: создание условий для возникновения у обучающихся внутренней потребности включения в учебную деятельность.
|
|
|
Приветствует учащихся,проверяет готовность учащихся к уроку (у каждого на столе лежит рабочая карта урока «План действий» и набор моделей прямоугольника, двух прямоугольных трапеций и одной разносторонней трапеции), создает комфортную атмосферу, настраивает учащихся на дальнейшее сотрудничество.
Девиз урока:
«Дойти можно лишь тогда, когда идешь,
узнать можно лишь тогда, когда учишься».
Вьетнамская пословица
-Как вы понимаете данное высказывние?
|
Приветствуют учителя,проверяют наличие необходимых учебных принадлежностей, настраиваются на деловой ритм, отвечают на вопросы учителя.
|
|
Личностные:
- формирование готовности к выполнению норм и требований в школьной жизни прав и обязанностей ученика
Коммуникативные:
- умение выражать свои мысли в соответствии с условиями коммуникации,
- умение передавать информацию интонацией,
- умение слушать,
- планирование учебного сотрудничества с учителем и сверстниками
|
II
Актуализация и фиксирование индивидуального затруднения в пробном действии
Цель: организовать выполнение обучающимися пробного учебного действия, организовать фиксирование индивидуального затруднения.
|
Среди изображенных фигур выберите трапеции
-Сформулируйте определение трапеции
-Назовите выделенные элементы трапеции
-Верно ли предложение: «высотой прямоугольной трапеции является его меньшая боковая сторона»?
|
|
Организует актуализацию знаний через фронтальный опрос (чертежи даны на доске).
|
Отвечают на вопросы учителя.
|
Знание определения трапеции, её элементов, умение «читать чертеж».
|
Познавательные:
умение строить логические цепочки,
анализировать объекты с целью выделения признаков,
умение сравнивать, подведение под понятие,
выдвижение гипотез и их обоснование
Личностные:
формирование потребности в самовыражении и самореализации
Коммуникативные:
умение задавать вопросы, слушать и понимать речь других,
формулирование собственного мнения
|
III
Постановка проблемной ситуации.
Выявление места и причины затруднения
Цель:
выявить место затруднения;
зафиксировать во внешней речи причину затруднения.
|
Как мне рассчитать количество плиток, если площадь одной из них 0,16 кв.м, а размеры комнаты указаны на рисунке?
|
|
-Почему сегодня на уроке мы начали разговор о трапеции? Дело в том, что в моей квартире прихожая имеет трапециевидную форму, а мне нужно выложить пол паркетной плиткой.
-А умеете ли вы вычислять площадь трапеции?
Действительно, мы с вами в повседневной жизни чаще всего встречаемся с квартирами и комнатами, и окнами в них прямоугольной формы. Вычислить площадь пола или окна нам не составляет труда. Однако,современная архитектура все чаще предлагает неправильные формы, например, форму трапеции. Как найти площадь такой фигуры? Знаете ли вы формулу для вычисления площади трапеции?
Сегодня мы с вами, опираясь на ваш личностный опыт и знания, откроем для себя формулу вычисления площади трапеции.
Итак, тема нашего урока «Площадь трапеции»
Какова же главная цель нашего урока?
Формирование умений расчета площади объектов в форме трапеции
|
Выдвигают свои гипотезы и приходят к выводу, что им не хватает знаний формулы площади трапеции.
Учащиеся формулируют цель урока, учитель корректирует
|
|
Познавательные:
самостоятельное выделение и
формулирование проблемы.
Личностные:
способность к самооценке на основе критерия успешной деятельности.
Волевая саморегуляция в ситуации затруднения.
Регулятивные:
умение перераспределять учебную задачу для себя
Коммуникативные:
умение оформлять свои мысли в устной и письменной форме
|
IV
Построение проекта выхода из затруднения
Цель: организовать постановку цели данного этапа урока;
организовать составление совместного плана действий;определить средства.
|
|
|
Организует учащихся по исследованию проблемной ситуации в виде поисковой беседы.
-Что мы должны сделать, чему научиться, чтобы достичь этой цели?
(учитель корректирует формулировку задач урока и открывает соответствующий слайд)
1. Вывести формулу для вычисления площади трапеции
2. Научиться вычислять площадь различных объектов, имеющих форму трапеции
|
Ведут поисковую беседу.
Формулируют задачи урока
|
|
Познавательные:
моделирование ситуации, построение логической цепи рассуждений, выдвижение гипотез и их обоснование
Регулятивные:
умение планировать и
прогнозировать
|
«Открытие нового знания»
|
Задания в приложении лист План действий.
|
|
Работать мы будем по плану (лежит у каждого на столе)
-Сначала вспомним то, что уже знаем
-Теперь выведем формулу площади прямоугольной трапеции
-И, наконец, выведем формулу площади произвольной трапеции
-Итак, площадь любой трапеции равна…….
|
Заполняют индивидуальную рабочую карту, при необходимости совещаясь с соседом по парте, сверяют свои ответы с правильными на слайде презентации.
Делают выводы о том, как вычислить площадь прямоугольной трапеции и произвольной трапеции
|
Знание формул площадей прямоугольника, прямоугольного треугольника; умение выполнять преобразования и выносить общий множитель за скобки.
|
Коммуникативные:
умение сотрудничать в поиске и выборе способа решения возникшей проблемы
|
V
Реализация построенного проекта
Цель: реализовать построенный проект в соответствии с планом; зафиксировать новое знание в речи и знаках; организовать устранение и фиксирование преодоления затруднения.
|
|
|
Организует реализацию построенного проекта в соответствии с планом. Организует подводящий диалог.
Организует фиксирование нового знания в речи и знаках.
-Итак, мы с вами в процессе работы вывели формулу для вычисления площади любой трапеции. Обычно говорят и пишут так:.. (учитель демонстрирует различные формы записи и чтения формулы площади трапеции).
-Теперь, я думаю, мы сможем с вами рассчитать количество плиток для пола в прихожей (учитель переходит к слайду с задачей)
|
Отвечают на вопросы учителя.
Фиксируют новое знание в речи и знаках.
Выполняют задание устно.
Решают задачу с комментированием.
|
Формула для вычисления площади трапеции.
|
Познавательные:
умение добывать новые знания, находить ответы на вопросы, используя учебник, свой жизненный опыт и информацию, полученную на уроке
Коммуникативные:
умение оформлять свои мысли в устной форме; слушать и понимать речь других
Регулятивные:
умение работать по коллективно составленному плану
|
VI
Первичное закрепление с проговариванием во внешней речи
Цель: организовать усвоение учениками нового способа действий с проговариванием во внешней речи.
Развитие умственных действий.
|
Вычислите площадь окна шириной 1,2 м,
высотой слева 1,4 м, а справа 1, 6 м.
№ 480(а)
№ 518(а)
|
№ 480(б)
|
Устанавливает осознанность восприятия учебного материала.
-Давайте решим еще одну практическую задачу.
Учитель организует работу по созданию математической модели задачи, начиная с построения чертежа и устанавливая соответствие между размерами окна и элементами трапеции.
Рассматривается решение типовых задач из учебника.
|
Учащиеся под руководством учителя создают математическую модель задачи, решают ее и сверяют ответ с правильным.
|
Формула для вычисления площади трапеции.
|
Познавательные:
Умение
структурировать знания, выбирать способы решения задач, умение строить речевое высказывание, рефлексия способов и условий действия
Личностные:формирование потребности в самовыражении и в социальном признании
Регулятивные:
умение оценивать правильность выполнения действий и вносить коррективы
Коммуникативные:
Умение оформлять свои мысли в устной и письменной форме; слушать и понимать речь других
|
VII
Самостоятельная работа по эталону
Цель: организовать выполнения обучающимися самостоятельной работы на новое знание и самопроверку по эталону и самооценку.
Организовать места и причины затруднений, работу над ошибками.
|
Задания в приложении и на слайде презентации.
|
|
Предлагает выполнить самостоятельную работу, проверить по образцу(лист контроля)
Предлагает оценить себя(лист самооценки)
Выставляет отметки.
-Наши исследования закончены.
Достигли ли мы цели и задач урока?
Проверим, насколько хорошо вы усвоили новые знания.
|
Выполняют самостоятельную работу, находят ошибки, вносят коррекцию, оценивают себя
|
Знание формулы площади трапеции.
|
Познавательные:умение осуществлять контроль, коррекцию, выделение и осознание того, что уже усвоено
и что ещё подлежит усвоению,
осознание качества и уровня усвоения.
Личностные: способность к самооценке на основе критерия успешности учебной деятельности
Регулятивные: уметь планировать действие в соответствии с поставленной задачей,
уметь вносить необходимые коррективы в действие после его завершения на основе его оценки и учёта характера сделанных ошибок
Коммуникативные: уметь оформлять свои мысли в письменной и устной форме
|
VIII
Рефлексия учебной деятельности на уроке
Цель: зафиксировать новое содержание урока;организовать рефлексию и самооценку обучающимися собственной учебной деятельности.
|
|
|
Организует рефлексию.
Используется лист Оцени себя сам.
Организует самооценку учебной деятельности
|
Осуществляет рефлексию
|
|
Личностные:
способность к самооценке на основе критерия успешности учебной деятельности
Регулятивные:умение проговаривать последовательность действий на уроке, оценивать правильность выполнения действия на уровне адекватной оценки
Коммуникативные: умение с
достаточной полнотой и
точностью выражать свои мысли
|
IX
Домашнее задание
Цель:
Закрепить полученные знания, устранить проблемы.
|
П.53, рассмотреть теорему о площади трапеции.
№ 518(а)
|
№ 518(б)
Творческое задание: составить кроссворд или синквейн.
|
Формирует д/з по различным уровням сложности в зависимости от результатов первичного закрепления.
|
|
|
Регулятивные:
уметь оценивать учебные действия в соответствии с поставленной задачей;
уметь прогнозировать предстоящую работу (составлять план)
Личностные:способность к самооценке на основе критерия успешности учебной деятельности
| |
 Скачать 147 Kb.
Скачать 147 Kb.
 ысота трапеции – 1) отрезок, 2) проведен из любой вершины на противолежащее основание или его продолжение, 3) перпендикулярен противолежащему основанию.
ысота трапеции – 1) отрезок, 2) проведен из любой вершины на противолежащее основание или его продолжение, 3) перпендикулярен противолежащему основанию.


 S =½(a + b)h
S =½(a + b)h