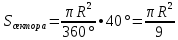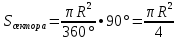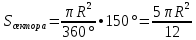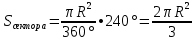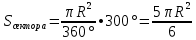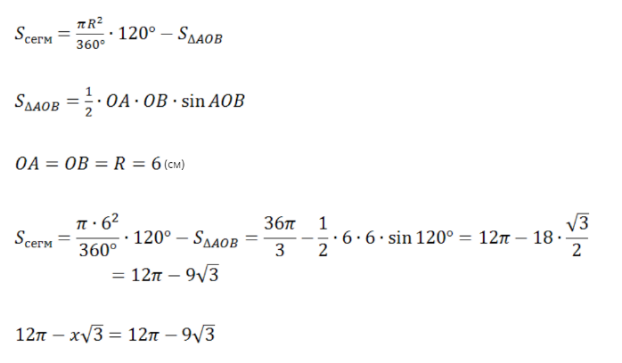|
|
КСП геометрия 7 класс. Г9 на 30.03.23. Площади круга, сектора и сегмента
Раздел:
|
9.4А Окружность. Многоугольники.
|
ФИО педагога
|
Юнусова А.В.
|
Дата:
|
30.03.2023
|
Класс: 9
|
Количество присутствующих:
|
Количество отсутствующих:
|
Тема урока
|
Площади круга, сектора и сегмента
|
Цели обучения в соответствии
с учебной программой
|
9.1.1.1 выводить и применять формулу длины дуги
9.1.1.2 выводить и применять формулу площади сектора, сегмента.
|
Цели урока
|
- знать формулу для расчета площадей круга и его частей
- решать простейшие задачи на вычисление площади круга и его частей
|
Ход урока
|
Этап урока/ Время
|
Действия педагога
|
Действия ученика
|
Оценивание
|
Ресурсы
|
Начало урока
7 мин
|
Организационное начало
Создание благоприятного психологического климата в классе.«Просто улыбнись»
Актуализация опорных знаний.
Выполните задания
1. Длина дуги окружности с градусной мерой вычисляется по формуле:
а) 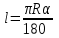 ; б) ; б)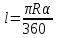 ; в) ; в)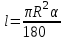 . .
2. Дана окружность радиуса 12 см . Чему равна длина ее дуги с градусной мерой 60°?
А) 4 см В) 6 см С) 8 см D) 12 см
3. Длина дуги окружности с радиусом 12 см и градусной мерой 100 равна:
а) 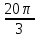 см; б) см; б) 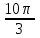 см; в) см; в) 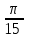 см. см.
4. Вычислите периметр фигуры
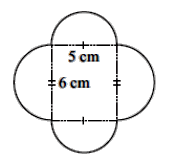 ответ: 34.6 cm ответ: 34.6 cm
|
Включаются в деловой ритм урока
Учащиеся выполняют самостоятельную работу и обмениваются друг с другом для проверки.
Демонстрируют знания, умения применение формулы площади круга
|
Взаимооценивание
|
Приложение 1
|
Середина урока
8 мин
13 мин
12 мин
|
Изучение нового материала
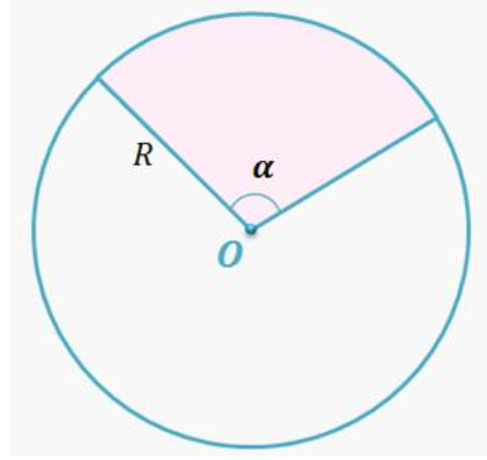
сектор — это часть круга ограниченная двумя радиусами.
площадь сектора с центральным углом n0 и радиусом r.

сегмент — это часть круга ограниченная хордой.
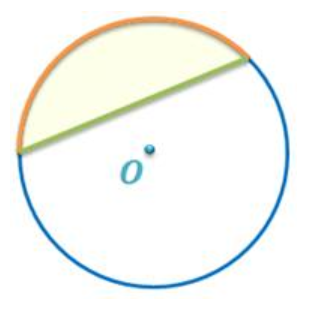
площадь сегмента находится как разность (или сумма) площади сектора и площади равнобедренного треугольника.
1 случай:
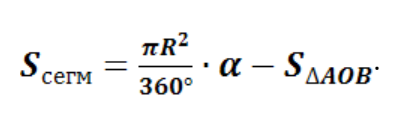
2 случай:
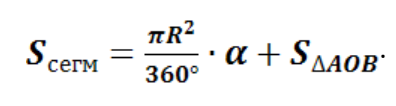
Первичное закрепление
Вычислить площадь сектора, соответствующего центральному углу в 300, радиусом 4см.
Ответ: 4,2см2.
Вычислить площадь сегмента, соответствующего центральному углу в 300, и радиусом 4см.
Ответ: 0,19 см2
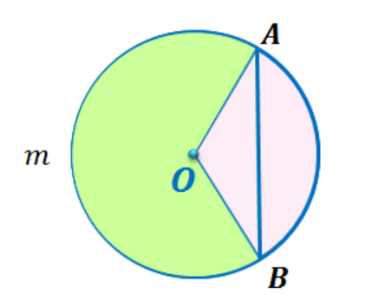
Найти площадь меньшего сегмента, стягиваемого дугой АВ, если треугольник АВС равносторонний, вписанный в окружность радиуса R.
Р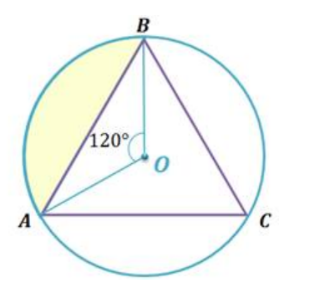 ЕШЕНИЕ: Тогда площадь меньшего сегмента, основанием которого служит сторона AB треугольника, равна. ЕШЕНИЕ: Тогда площадь меньшего сегмента, основанием которого служит сторона AB треугольника, равна.
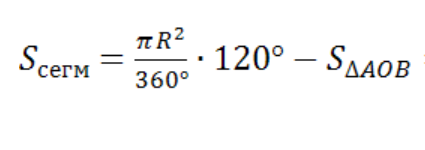
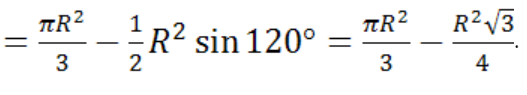
Парная работа
1.Найти площадь сектора, соответствующего центральному углу в
а)400
б)900
в)1500
г)2400
д)3000
РЕШЕНИЕ:
а) 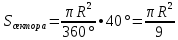
б) 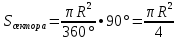
в) 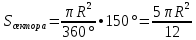
г) 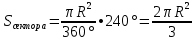
д) 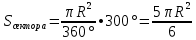
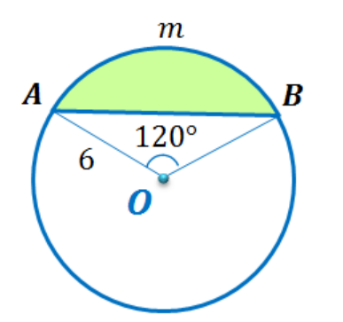
2.Чему равен х, если площадь сегмента АmВ равна 12π-х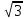 , радиус равен 6 и центральный угол 1200? , радиус равен 6 и центральный угол 1200?
 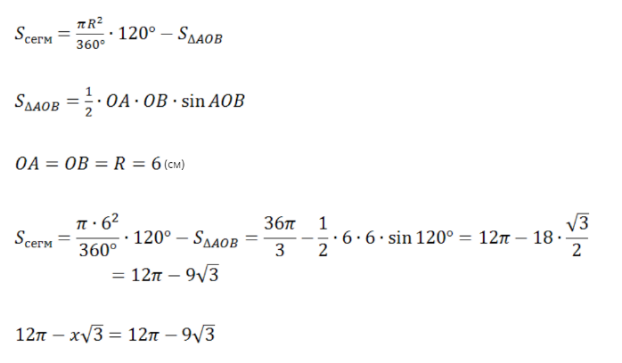
|
совместно с учащимися определить тему урока, цели урока
участвуют в работе анализируют, воспринимают информацию учителем, делают соответствующие записи в тетрадь.
Работа у доски комментированное решение
Деление на пары
Работа в парах, идет взаимное обучение друг друга
|
Самооценивание
Взаимооценивание
Дескриптор
-применяют площадь квадрата
-применяет формулу площади сектора DАКС
-вычисляет площадь треугольника и
площадь сегмента АКС
- вычисляют площадь серна
|
Приложение 2
Приложение 3
|
Конец урока
5 мин
|
Итог урока
Рефлексия
Домашняя работа:
|
Анализируют работу на уроке
|
Самооценивание
|
Карточки
|
Приложение 1.
1. Длина дуги окружности с градусной мерой вычисляется по формуле:
а) 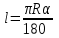 ; б) ; б)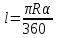 ; в) ; в)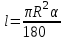 . .
2. Дана окружность радиуса 12 см . Чему равна длина ее дуги с градусной мерой 60°?
А) 4 см В) 6 см С) 8 см D) 12 см
3. Длина дуги окружности с радиусом 12 см и градусной мерой 100 равна:
а) 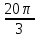 см; б) см; б) 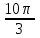 см; в) см; в) 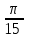 см. см.
4. Вычислите периметр фигуры

Приложение 2.
Вычислить площадь сектора, соответствующего центральному углу в 300, радиусом 4см.
Вычислить площадь сегмента, соответствующего центральному углу в 300, и радиусом 4см.
Найти площадь меньшего сегмента, стягиваемого дугой АВ, если треугольник АВС равносторонний, вписанный в окружность радиуса R.
Приложение 3.
Парная работа
1.Найти площадь сектора, соответствующего центральному углу в
а)400
б )900 )900
в)1500
г)2400
д)3000
2.Чему равен х, если площадь сегмента АmВ равна 12π-х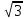 , радиус равен 6 и центральный угол 1200? , радиус равен 6 и центральный угол 1200? |
|
|
 Скачать 0.55 Mb.
Скачать 0.55 Mb.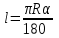 ; б)
; б)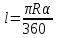 ; в)
; в)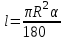 .
.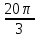 см; б)
см; б) 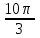 см; в)
см; в) 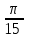 см.
см.
 )900
)900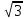 , радиус равен 6 и центральный угол 1200?
, радиус равен 6 и центральный угол 1200?




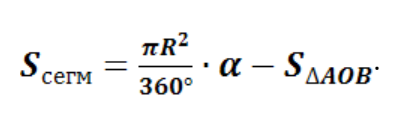
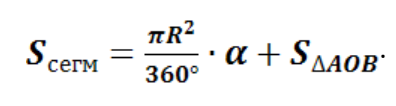
 ЕШЕНИЕ:
ЕШЕНИЕ: