Плоскости в пространстве Взаимное расположение плоскостей
 Скачать 56.62 Kb.
|
|
Министерство здравоохранения Забайкальского края ГПОУ «Борзинское медицинское училище (техникум)» Специальность : Сестринское дело СООБЩЕНИЕ «Плоскости в пространстве: Взаимное расположение плоскостей» Автор: студентка группы С-003 Костырева Вероника Руководитель-консультант: Уваровская Мария Викторовна Пространство – это множество, элементами которого являются точки и в котором выполняется система аксиом стереометрии, описывающая свойства точек, прямых и плоскостей. Система аксиом стереометрии дает описание свойств пространства и основных его элементов. Понятия «точка», «прямая» и «плоскость» принимаются без определений: их описание и свойства содержатся в аксиомах. С другой стороны, понятия «точка», «прямая», «плоскость» имеют наглядный смысл, отраженный на чертежах и рисунках. Изучение пространства приводит к необходимости расширить систему аксиом планиметрии и рассмотреть новую группу аксиом, в которых выражены свойства взаимного расположения точек, прямых и плоскостей, что особенно важно для нас, в пространстве. 2. Способы задания плоскости Изучение пространства приводит к необходимости расширить систему аксиом. Рассмотрим аксиому R1. В пространстве существуют плоскости. В каждой плоскости пространства выполняются все аксиомы планиметрии. Эта аксиома дает нам право рассматривать в любой плоскости пространства отрезки, прямые со всеми их свойствами, которые изучались в планиметрии. Например, если прямая а и не принадлежащая ей точка М лежат в некоторой плоскости α, то в этой плоскости можно провести через точку М прямую, параллельную прямой а, и притом только одну. 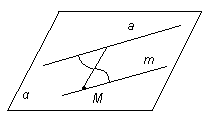 В аксиоме R3 говорится: какова бы не была плоскость, существуют точки, принадлежащие этой плоскости, и точки, не принадлежащие ей. Данной аксиомой утверждается, что для любой плоскости в пространстве можно выбрать любое количество точек в этой плоскости, равно как и сколько угодно точек вне её. В случае, если точка А лежит в (принадлежит) плоскости α, то записывают: А 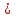 α и говорят, что плоскость α проходит через точку А. 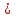Если точка А не принадлежит плоскости α, то записывают: А α и говорят, что плоскость α не проходит через точку А.Плоскость в пространстве однозначно определяется: - тремя точками, не лежащими на прямой. Аксиома R2 (аксиома плоскости) гласит: Через любые три точки, не принадлежащие одной прямой, можно провести плоскость, и притом только одну. Плоскость, которая проходит через точки А, В и С, не принадлежащие одной прямой (С 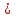АВ), обозначается символически (АВС); если этой плоскостью является плоскость α, то пишут α = (АВС) или (АВС)= α. Стол, имеющий три ножки, не может качаться на плоском полу. Его устойчивость объясняется тем, что концы трех его ножек (три точки) принадлежат одной плоскости – плоскости пола, но не принадлежат одной прямой. Плохо сделанный стол на четырех ножках качается на плоском полу, и под одну из его ножек что-нибудь стараются подложить.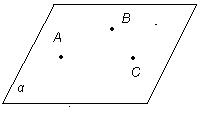 - прямой и точкой, не лежащей на прямой. По теореме 1 через любую прямую и не принадлежащую ей точку можно провести плоскость, и притом только одну. 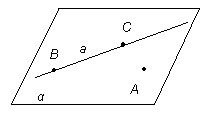 Доказательство. Пусть даны прямая а и не принадлежащая ей точка А. Выберем на прямой а любые точки В и С. Через точки В и С проходит только одна прямая – прямая а. Так как точка А по условию теоремы не принадлежит прямой а, то точки А, В и С не принадлежат одной прямой. По аксиоме R2 через точки А,В,С проходит только одна плоскость – плоскость АВС, которую обозначим α. Прямая а имеет с ней две общие точки – точки В и С, следовательно по аксиоме R4 (аксиоме прямой и плоскости - Если прямая проходит через две точки плоскости, то она лежит в этой плоскости) эта прямая лежит в плоскости α. Таким образом, плоскость α проходит через прямую а и точку А и является искомой. Докажем, что другой плоскости, проходящей через прямую а и точку А 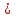а, не существует.Предположим, что есть другая плоскость – α 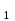 , проходящая через точку А и прямую а. Тогда плоскости α и α проходят через точки А, В и С, не принадлежащие одной прямой, а значит совпадают. Следовательно, плоскость α единственная. Теорема доказана. Две прямые в пространстве называются пересекающимися, если они имеют ровно одну общую точку. Теорема 2. Через любые две пересекающиеся прямые можно провести плоскость, и притом только одну. 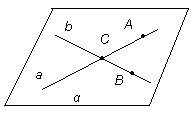 Доказательство. Пусть данные прямые а и b пересекаются в точке С. Выберем на прямых а и b любые точки А и В, отличные от С: А 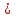а, В b. Тогда точки А, В и С не принадлежат одной прямой, и по аксиоме R2 через них можно провести только одну плоскость. Обозначим её α.Точки А и С прямой а принадлежат плоскости α, значит, плоскость α проходит через прямую а (аксиома R4: Если прямая проходит через две точки плоскости, то она лежит в этой плоскости). Плоскость α проходит и через прямую b, так как точки В и С этой прямой принадлежат плоскости α. Таким образом, плоскость α проходит через прямые а и b, следовательно является искомой. Докажем единственность плоскости α. Допустим, что есть другая, отличная от плоскости α и проходящая через прямые а и b, плоскость β. Так как плоскость β проходит через прямую а и не принадлежащую ей точку В, то по теореме 1 она совпадает с плоскостью α. Единственность плоскости α доказана.  Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются. 3. Взаимное расположение плоскостей в пространстве При взаимном расположении двух плоскостей в пространстве возможен один из двух взаимно исключающих случаев. Две плоскости имеют общую точку. Тогда по аксиоме пересечения двух плоскостей они имеют общую прямую. Аксиома R5 гласит: если две плоскости имеют общую точку, то пересечение этих плоскостей есть их общая прямая. Из этой аксиомы следует, что у плоскостей Такие плоскости называются пересекающимися. 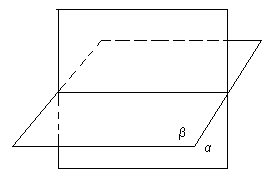   2. Две плоскости не имеют общей точки.  α  β Две плоскости совпадают β α |