Ответы на вопросы гидромеханики. Гидромеханика. Плотность

• Название: Плотность
• Анкор: Ответы на вопросы гидромеханики
• Дата: 07.10.2022
• Размер: 0.83 Mb.
• Имя файла: Гидромеханика.docx
• Тип: Закон; #719291

1. 
   изучение основных законов движения и равновесия жидкостей, капельных и газообразных, а также их силового взаимодействия с твердыми телами.
   

2.1



Плотность — это отношение массы вещества к его объему:

р = m/V

На плотность жидкости влияют температура и давление.

2.2



2.3.свойство жидкости изменять свой объем при изменении температуры. С ростом температуры объем жидкости увеличивается и наоборот. Различные жидкости при увеличении температуры на одну и ту же величину увеличиваются в объеме по разному. Поэтому свойство жидкости увеличиваться в объеме с увеличением температуры характеризуется коэффициентом температурного расширения Bт, который показывает изменение единицы объема данной жидкости при изменении ее температуры на 1 К.

β_р=(-dV/V₀)·(1/dp),

2.4 Коэффициентом температурного расширения жидкости β_t – называется относительное изменение объема жидкости, при изменении температуры на единицу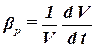



2.5Поверхностное натяжение При контакте капельной жидкости с другой капельной жидкостью, газом или твердым телом молекулы жидкости, находящиеся на поверхности находятся в условиях, которые отличаются от условий в которых находятся молекулы внутри жидкости, т.к. последних окружают молекулы со всех сторон. Вследствие этого, энергия поверхностных молекул отличается от энергии молекул в объеме жидкости на величину, называемую поверхностной энергией. Эта энергия пропорциональна площади поверхности раздела S Эn = σS, (1.18) где σ - коэффициент поверхностного натяжения, зависящий от природы соприкасающихся сред. Коэффициент поверхностного натяжения можно представить в виде σ = F/ l, (1.19) где F - сила поверхностного натяжения; l - длина линии, ограничивающей поверхность раздела. Поверхностное натяжение жидкости чувствительно к ее чистоте и температуре. При увеличении температуры поверхностное натяжение жидкости уменьшается, а в критической точке, где отсутствует различие между паром и жидкостью равно 0. Вещества способствующие повышению поверхностного натяжения называются поверхностно-активные вещества (ПВА).

2.5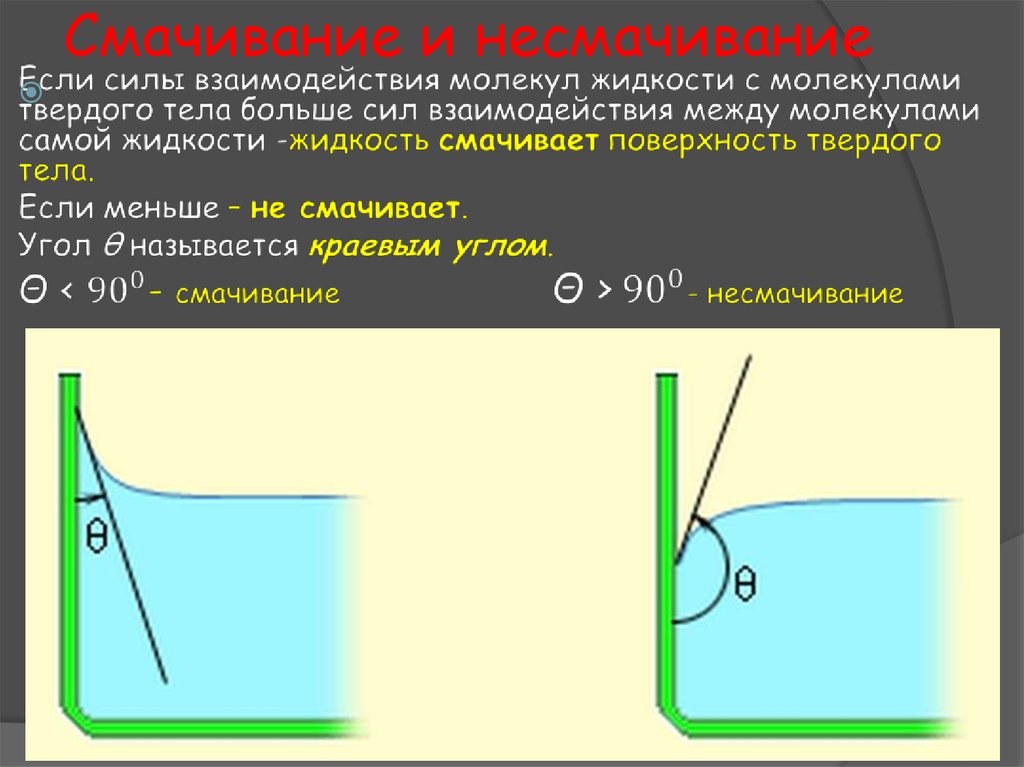



3)Свойство жидкостей оказывать сопротивление сдвигу называется вязкостью. При движении жидкости происходит относительное перемещение частиц, что приводит к появлению силы трения между ними, причем количественное значение ее пропорционально вязкости жидкости



4) называют жидкость, при течении которой её вязкость зависит от градиента скорости^[1][2]. Обычно такие жидкости сильно неоднородны и состоят из крупных молекул, образующих сложные пространственные структуры.

5.1) Из механики твердого тела известно, что в том случае, если на тело не действуют внешние силы или их сумма равна нулю, то тело находится в состоянии покоя или прямолинейного равномерного движения. Данное утверждение полностью справедливо и для жидкости. В этом случае отсутствует взаимное перемещение частиц жидкости и такое состояние массы жидкости называется равновесным. Все внешние силы, действующие на жидкость, можно разделить на поверхностные и объемные (массовые). К поверхностным силам относятся силы, действующие в точках граничной поверхности данной массы. Их величина пропорциональна площади поверхности Δ Р = р Δω, (2.1) где Δω - площадь поверхности, на которую действует сила; р - величина напряжения. Объемные силы представляют собой внешние силы , величина которых пропорциональна объему жидкости Δ R = k ΔW, (2.2) где ΔW - объем рассматриваемой массы жидкости; k = ρj - коэффициент пропорциональности; j - ускорение данной объемной силы

5.2) Величина гидростатического давления определяется как отношение сжимающей силы ΔР к величине площадки Δω: Р = ΔР/Δω. (2.3) При стремлении Δω→0 получаем гидростатическое давление в точке. Основная теорема гидростатики утверждает, что величина гидростатического давления в данной точке не зависит от ориентации в пространстве площадки, на которой она расположена: Рх = Py = Pz = Pn, (2.4) где Рх , Py ,Pz , Pn - гидростатические давления по направлению координатных осей и в произвольном направлении.

6.1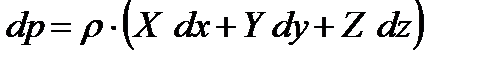



6.2 Поверхностью уровня называются такие поверхности, в каждой точке которых данная функция координат (параметр) имеет одинаковое значение. К поверхностям уровня относятся поверхности равной температуры, равного давления, равной плотности и др. В гидромеханике наиболее часто требуется определить поверхности равного давления.

Основные свойства поверхностей уровня:

1. Две поверхности уровня не пересекаются между собой.

2. Внешние объемные силы направлены нормально к поверхности уровня.

7.1 Это уравнение, позволяю­щее определить давление р в любой точке покоящейся жидкости

7.2 Абсолютное значение

Абсолютное давление ─ это истинное давление жидкостей, паров или газов, которое отсчитывается от абсолютного нуля давления (абсолютного вакуума).

Избыточное давление

Разность между абсолютным давлением p и атмосферным давлением p_а называется избыточным давлением и обозначается р_изб:

р_изб = p - p_а

или

р_изб/γ = (p - p_а)/γ = h_п

h_п в этом случае называется пьезометрической высотой, которая является мерой избыточного давления.

На рисунке показан закрытый резервуар с жидкостью, на поверхности которой давление p_0. Подключенный к резервуару пьезометр П (см. рис. ниже) определяет избыточное давление в точке А.

Абсолютное и избыточное давления, выраженные в атмосферах, обозначаются соответственно ата и ати.

Вакууметрическое давление

Вакуумметрическое давление, или вакуум, — недостаток давления до атмосферного (дефицит давления), т. е. разность между атмосферным или барометрическим и абсолютным давлением:

р_вак = p_а - p

или

р_вак/γ = (p_а - p)/γ = h_вак

где h_вак — вакуумметрическая высота, т. е. показание вакуумметра В, подключенного к резервуару, показанному на рисунке ниже. Вакуум выражается в тех же единицах, что и давление, а также в долях или процентах атмосферы.

8) при равновесии несмешивающихся жидкостей поверхности их разде­ла будут горизонтальными плоскостями.

Жидкости при этом расположатся по высоте (считая сверху вниз) в порядке воз­растания их плотностей, что следует не­посредственно из общих условий устой­чивого равновесия механической систе­мы в поле тяготения: центр тяжести системы расположенные в наиболее низкой точке, или, иначе, потенциальная энергия системы должна быть минимальной.

9) Под относительным равновесием понимают такое движение жидкости, при котором все частицы жидкости не совершают относительного движения и вся масса жидкости движется как твердое тело. Таким образом, в условиях спуска по вертикали с ускорением γu, в подвижной системе координат удельный вес уменьшается, а при свободном падении γ = g и наблюдается условие невесомости.

10) Вращающие стенки цилиндра приведут во вращательное движение ближайшие к стенкам слои жидкости, а затем, в следствие вязкости жидкости - и всю ее массу, которая приобретет угловую скорость ω. Для определения формы поверхности уровня воспользуемся общим дифференциальным уравнением поверхности уровня. На частицы жидкости действуют две объемные силы: силы инерции и силы земного тяготения. В точке М центробежное ускорение определится, как γu = ω² x. (2.40)

Полное ускорение внешних объемных сил: γu =Корень(( ω² x)² + g²))

11) сила, с которой жидкость действует на плоскую стенку, равна весу жидкости в объеме цилиндра с основанием, равным площади данной стенки, и высотой, равной глубине погружения центра тяжести этой площадки под уровень свободной поверхности. Точка приложения результирующей силы давления жидкости на любую поверхность называется центром давления.

момент равнодействующей силы относительно произвольной оси равен сумме моментов составляющих сил относительно той же оси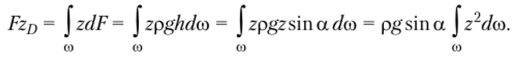



13)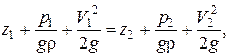



Таким образом, энергетический смысл уравнения Бернулли заключается в следующем: при установившемся движении элементарной струйки жидкости сумма трех удельных энергий (энергии положения, энергии давления и кинетической энергии) остается неизменной для любого сечения элементарной струйки жидкости.

Для реальной жидкости:

Альфа- коэффициент Кориолиса, который учитывает неравномерность распределения скоростей, в поперечном сечении потока.

Скоростная высота- Данную величину можно представить как высоту, на которую поднимется жидкость, начавшая двигаться вертикально со скорость u при отсутствии сопротивления движению.

15) Уравнение Бернулли находит самое широкое применение в технике. Работа ряда устройств и приборов основана на использовании этого важнейшего закона гидравлики. Этот измерительный прибор имеет ряд достоинств. Он прост в изготовлении и эксплуатации (в нем отсутствуют какие-либо движущиеся части), имеет низкую стоимость, характеризуется незначительными потерями напора. Прибор можно использовать для измерения расхода как однородных, так и неоднородных жидкостей, широко применяется в лабораторных и промышленных условиях. Трубчатый расходомер Вентури (рис. 2.15) состоит из плавно сужающегося участка трубы (сопла), соединенного цилиндрической вставкой с постепенно расширяющимся участком (диффузором). Скорость потока в суженном участке возрастает, а давление падает. Возникает перепад давлений, который можно измерить двумя пьезометрами или дифференциальным манометром. Разность давлений Р И, скорость и расход жидкости находятся в определенной зависимости, которая может быть получена из уравнения Бернулли для двух сечений I—I и II—И. Средняя скорость в сечении II—II





Расход жидкости в трубопроводе определяется по следующей формуле:



Учитывая неравномерность распределения скоростей в сечении потока, а также неизбежные потери напора за счет сопротивлений внутри приборов, действительный расход несколько отличается от расхода, определяемого по формуле. Поэтому вводят коэффициент т, учитывающий влияние указанных факторов. Этот коэффициент т устанавливается опытным путем на основании ряда предварительных измерений расходов при различных скоростях и вводится в уравнение: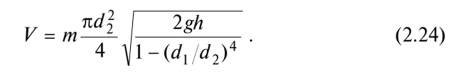



Учитывая, что почти все величины, входящие в формулу (2.24), имеют постоянные значения, заранее можно вычислить постоянную расходомера: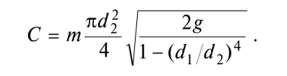

В результате уравнение (2.24) упростится:



16) Уравнение Бeрнуллидля газав простейшем виде записы­вается так:

p_пр.п1 = p_пр.п2+ Dp_пот ,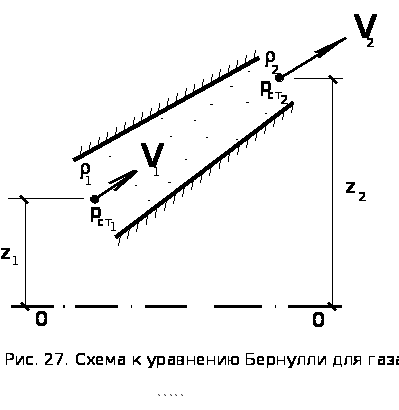


Уравнение Бeрнулли в традиционной записи получим, если в по­следнем ра­

венстве раскроем значения приведённых полных давлений p_пр.п1 и p_пр.п2:

(скорости в квадратах)
СВЕРХЗВУКОВО́Е ТЕЧЕ́НИЕ, те­че­ние га­за, ско­рость v час­тиц ко­то­ро­го в рас­смат­ри­вае­мой об­лас­ти боль­ше ме­ст­но­го зна­че­ния ско­ро­сти зву­ка a. Ско­рость зву­ка за­ви­сит от темп-ры; при 0 °С в воз­ду­хе a=331 м/с. С. т. на­блю­да­ют­ся при об­те­ка­нии воз­ду­хом не­ко­то­рых ле­тя­щих са­мо­лё­тов, ра­кет, арт. сна­ря­дов, вхо­дя­щих в ат­мо­сфе­ру КА и ме­тео­рои­дов, а так­же в по­то­ках, воз­ни­каю­щих в ре­ак­тив­ных дви­га­те­лях, тур­би­нах, тур­бо­ком­прес­со­рах, аэ­ро­ди­на­мич. тру­бах и др.

По­сколь­ку сла­бые воз­му­ще­ния в га­зе рас­про­стра­ня­ют­ся со ско­ро­стью зву­ка, в С. т. они не мо­гут рас­про­стра­нять­ся вверх по по­то­ку и сно­сят­ся вниз по по­то­ку, ос­та­ва­ясь внут­ри Ма­ха ко­ну­са. Вол­на, вы­зван­ная по­вы­ше­ни­ем дав­ле­ния (об­ра­зую­щая­ся, напр., при взры­ве), при v>а (Ма­ха чис­ло M>1) мо­жет иметь ма­лую тол­щи­ну фрон­та (по­ряд­ка дли­ны сво­бод­но­го про­бе­га мо­ле­кул). В этом слу­чае го­во­рят об удар­ной вол­не (скач­ке уп­лот­не­ния).

При об­те­ка­нии вы­пук­ло­го из­ло­ма пло­ской стен­ки (или тон­ко­го кли­на) твёр­до­го те­ла сверх­зву­ко­вым те­че­ни­ем иде­аль­но­го га­за воз­ни­ка­ет Пран­дт­ля – Май­е­ра те­че­ние. При об­те­ка­нии сверх­зву­ко­вым те­че­ни­ем пла­сти­ны под уг­лом ата­ки мень­ше не­ко­то­ро­го от её пе­ред­ней кром­ки вниз идёт пло­ский ска­чок уп­лот­не­ния, а ввер­ху над пла­сти­ной об­ра­зу­ет­ся те­че­ние раз­ре­же­ния, что при­во­дит к по­яв­ле­нию подъ­ём­ной си­лы. Од­но­вре­мен­но воз­ни­ка­ет ло­бо­вое со­про­тив­ле­ние, обу­слов­лен­ное по­яв­ле­ни­ем скач­ков уп­лот­не­ния и уве­ли­че­ни­ем эн­тро­пии га­за. По­вы­ше­ние эн­тро­пии в скач­ке свя­за­но с дис­си­па­ци­ей энер­гии во фрон­те удар­ной вол­ны за счёт вяз­ко­сти и те­п­ло­про­вод­но­сти. Чем бóль­шие воз­му­ще­ния вы­зы­ва­ет те­ло в га­зе, тем ин­тен­сив­нее удар­ные вол­ны и боль­ше со­про­тив­ле­ние дви­же­нию те­ла. Для умень­ше­ния со­про­тив­ле­ния, свя­зан­но­го с об­ра­зо­ва­ни­ем удар­ных волн при сверх­зву­ко­вых ско­ро­стях, в ле­та­тель­ных ап­па­ра­тах де­ла­ют стре­ло­вид­ные и тре­уголь­ные кры­лья, пе­ред­ние кром­ки ко­то­рых об­ра­зу­ют ост­рый угол с на­прав­ле­ни­ем ско­ро­сти на­бе­гаю­ще­го по­то­ка. Наи­мень­шее со­про­тив­ле­ние при С. т. име­ет тон­кое за­ост­рён­ное с кон­цов те­ло, дви­жу­щее­ся под ма­лы­ми уг­ла­ми ата­ки.

Число Маха - Важное значение числа Маха объясняется тем, что оно определяет, превышает ли скорость течения газовой среды (или движения в газе тела) скорость звука или нет. Сверхзвуковые и дозвуковые режимы движения имеют принципиальные различия; для авиации это различие выражается в том, что при сверхзвуковых режимах возникают узкие слои быстрого значительного изменения параметров течения (ударные волны), приводящие к росту сопротивления тел при движении, концентрации тепловых потоков у их поверхности и возможности прогорания корпуса тел и тому подобное.

{\displaystyle {\mathsf {M}}={\frac {v}{a}},}

M=v/a , где v-скорость потока, а-местная скорость звука

18)

ЛАМИНА́РНОЕ ТЕЧЕ́НИЕ (от лат. lamina  пластинка),течение жидкости или газа, при котором траектории частиц среды практически параллельны направлению осн. потока. В общем случае разл. слои жидкости или газа движутся с разными скоростями, причём в Л. т. отсутствует перемешивание соседних слоёв среды. Л. т. наблюдается в очень вязких жидкостях, а также при достаточно медленном обтекании жидкостью или газом тел малых размеров.

При увеличении скорости течения жидкости – скорость V увеличивается, градиент скорости 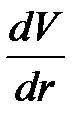  , соответственно. Увеличивается вращательное движение частиц, при этом скорость более удаленного от стенки слоя еще более увеличивается (рисунок 2.2), a скорость пристеночных слоев еще более уменьшается.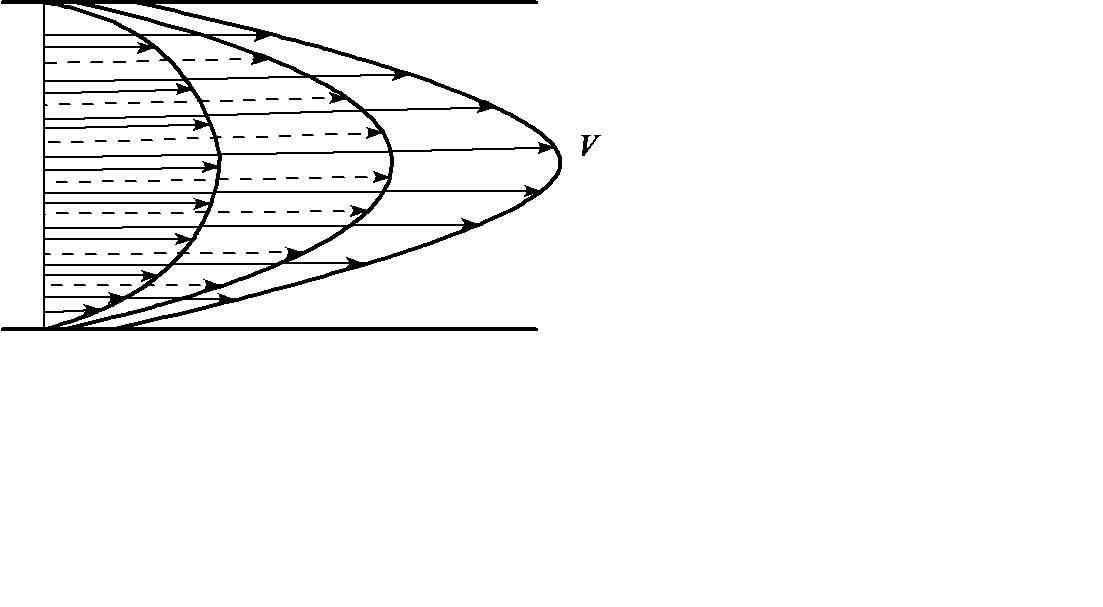


Критическая скорость, при которой ламинарное течение переходит в турбулентное, равна:

где K – универсальный коэффициент пропорциональности (он одинаков для всех жидкостей и диаметров труб); d – диаметр трубопровода.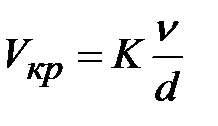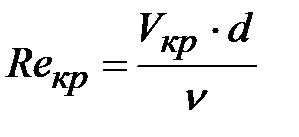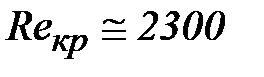