Контрольные работы Приложение к ПМ 02. Пм 02. Эксплуатация нефтегазопромыслового оборудования

• Название: Пм 02. Эксплуатация нефтегазопромыслового оборудования
• Дата: 16.11.2022
• Размер: 2.3 Mb.
• Имя файла: Контрольные работы Приложение к ПМ 02.doc
• Тип: Контрольная работа; #791712
• страница: 18 из 21

2.
Давление в сосуде с газом измеряется микроманометром, заполненным жидкостью плотностью . Трубка микроманометра установлена под углом  к горизонту. Определить, на сколько изменится давление в сосуде, если перемещение мениска в трубке составит b мм. (вправо или влево ).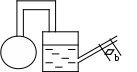

Величина Предпоследняя цифра шифра.
	1	2	3	4	5	6	7	8	9	0
 (кг/м3)	600	625	700	730	760	790	800	810	830	850
 0	10	15	20	30	35	40	45	10	15	20
b (мм)	2	4	6	8	5	1	4	3	2	1
Перемещение влево или вправо

№ 3.

Длинная труба с внутренним диаметром d, открытая по концам, погружена в вертикальном положении в резервуар с жидкостью плотность которой ₁. В верхний конец трубы залито m (кг) жидкости плотностью ₂. На какой высоте h над уровнем жидкости в резервуаре установится уровень жидкости в трубе?

Величины	Предпоследняя цифра шифра
	1	2	3	4	5	6	7	8	9	0
d (мм)	50	80	100	120	60	70	90	110	115	130
1 (кг/м3)	1000	1100	1120	1150	1180	1200	1250	1300	1350	1000
2 (кг/м3)	780	800	820	840	860	900	1000	850	870	830
m (кг)	3	5	7	9	2	4	6	8	10	12

№4

В запаянную с одного конца трубку залили некоторое количество жидкости с плотностью  и некоторое количество ртути (_рт=13650 кг/м³). Вычислить давление над жидкостью в трубке, если после погружения свободного конца трубки в вертикальном положении в чашку с ртутью, высота столба ртути оказалась h₁, а высота столба жидкости h_2.

Атмосферное давление принять равным 110⁵ Па

Величины	Предпоследняя цифра шифра
	1	2	3	4	5	6	7	8	9	0
h1 (мм)	500	510	512	514	516	518	520	550	560	570
h2 (мм)	300	310	320	330	340	350	360	370	380	390
 (кг/м3)	700	720	730	740	750	760	800	810	820	830

№5

Определить разность давлений в двух цилиндрах, заполненных жидкостью плотностью  и соединенных между собой дифференциальным ртутным манометром. До уровня ртути трубки заполнены жидкостью из цилиндров. Разность уровней ртути в манометре h. _рт=13650 кг/м³.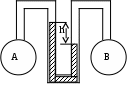

Величины	Предпоследняя цифра шифра
	1	2	3	4	5	6	7	8	9	0
h (мм)	200	250	300	350	280	260	325	375	400	410
 (кг/м3)	1000	800	850	1200	900	950	1250	750	755	760

№6

С целью определения удельного веса неизвестного сплава слиток его взвесили дважды: один раз в воздухе, другой раз, погрузив в воду.

Вес слитка в воздухе G₁

Вес слитка в воде G₂

Вычислить удельный вес сплава.

Величины	Предпоследняя цифра шифра
	1	2	3	4	5	6	7	8	9	0
G1 (H)	1500	1550	1600	1625	1640	1650	1660	1665	1675	1700
G2 (H)	1350	1400	1450	1475	1495	1490	1500	1520	1525	1550

Принять плотность воды _в=1000 кг/м³
№7

Вычислить вес колонны стальных труб длинной L (м), спущенных в скважину заполненную нефтью плотностью _н, если известно, что 1 погонный метр таких туб с муфтами в воздухе весит G’ (Н/м).

Плотность стали _ст=7850 кг/м³.

Величины	Предпоследняя цифра шифра
	1	2	3	4	5	6	7	8	9	0
L (м)	500	550	600	650	700	750	800	850	900	950
н(кг/м3)	850	900	845	890	870	880	895	885	875	855
G’ (Н/м)	22	24	26	28	30	21	23	25	27	29

№8

Удельный вес жидкости определяют погружением в неё поплавка.

Вес поплавка в воздухе G₁, вес поплавка погруженного в воду G₂, вес поплавка погруженного в исследуемую жидкость G₃. Вычислить удельный вес и плотность исследуемой жидкости.

Плотность воды принять _в=1000 кг/м³.

Величины	Предпоследняя цифра шифра
	1	2	3	4	5	6	7	8	9	0
G1 (Н/м)	420	430	440	450	610	630	650	670	700	720
G2 (Н/м)	300	310	320	330	490	510	530	550	580	600
G3 (Н/м)	340	350	360	370	510	540	560	580	610	630

№9.

Определить глубину погружения в жидкость с удельным весом ₁, бруска с размерами основания 400 х 1000 мм и высотой 300 мм, если плотность материала бруска ₂.

Величины	Предпоследняя цифра шифра
	1	2	3	4	5	6	7	8	9	0
1 (Н/м3)	10000	10100	10300	10500	10700	11000	11500	12000	12500	13000
2 (кг/м3)	510	550	530	580	600	620	640	660	700	720

№