Контрольные работы Приложение к ПМ 02. Пм 02. Эксплуатация нефтегазопромыслового оборудования
 Скачать 2.3 Mb.
|
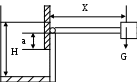
Объем вытесненной шаром жидкости равен объему погруженной части шара, т.е. половина его объема.Объем шара  Объем вытесненной жидкости  Выталкивающая сила (архимедова) равна весу вытесненной шаром жидкости.  Очевидно, что шар больше не погрузился в воду потому, что его вес оказался уравновешенным архимедовой силой, т.е.   Но вес шара Gm=Vmm; Откуда  Поставив выражения Vm и Gm Получим  н/м3Пример № 4. Прямоугольное отверстие размерами h х в в стенке резервуара с жидкостью плотностью , закрыто плоским щитом, вращающимся вокруг горизонтальной оси и прижимаемым к стенке грузом G на рычаге длиной X. Ось вращения щита находится на расстоянии от верхней кромки отверстия. Определить длину рычага Х, необходимую для удержания жидкости в резервуаре на заданном уровне Н. Резервуар не имеет крышки. Весом щита, рычага, а так же трением в шарнире пренебречь
РЕШЕНИЕ. Для поддержания заданного уровня жидкости Н, необходимо равенство моментов силы гидростатического давления жидкости на щит и веса груза действующего через рычаг. М1=Мg Здесь: Мf=F*l1, Mg=G*X Где F – сила гидростатического давления на щит F=gheS Здесь: he – глубина погружения центра тяжести щита he=Н-h/2 S – площадь смоченной поверхности щита S=в*h Тогда F=g(H-h/2)вh=1000 9,81(1,3-1/2) 1,2 *1=96000=96 кН. L – расстояние от оси вращения щита до центра давления. Для определения в необходимо определить глубину погружения центра давления lo.  здесь: Jc – момент инерции площади стенки 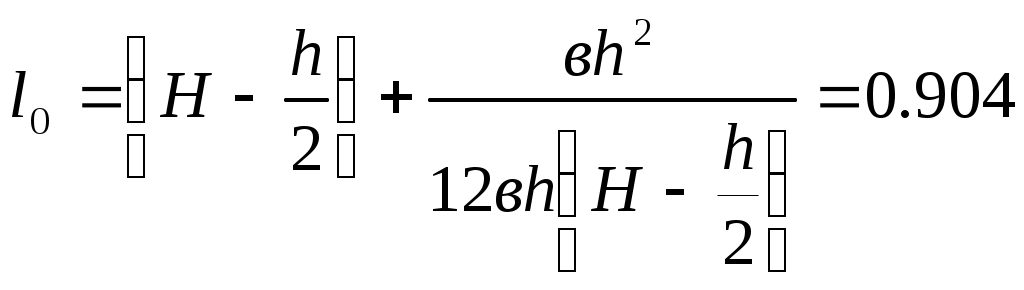  тогда l=(a+h)-(H-l0)=0.754 м т.к. Fl=GX то  м.Пример № 5. Определить силу избыточного давления F воды на наклонную боковую стенку и глубину погружения центра давления hс при следующих данных: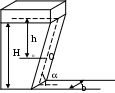 
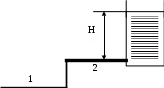
РЕШЕНИЕ. Сила избыточного давления F=S*ghc Где: S – площадь стенки S=d*l;  ;  hc – глубина погружения центра тяжести стенки.  тогда  расстояние от уреза жидкости до центра давления  где Jс – момент инерции площади стенки относительно оси проходящей через центр тяжести стенки. Для прямоугольной стенки с заданными размерами.  тогда  глубина погружения центра давления. h0=l0*sin=3.04*sin60=3.33 м Пример № 6. Трубопровод постоянного сечения состоит из 3-х участков длиной l1=50 м; l2=70 м; l3=100 м. Первый и третий участки горизонтальны, а 2-ой наклонен к горизонту под углом =600. Давление в начале трубопровода P1=1,5 мПа, а в конечной Р2=0,3 мПа. Определить гидравлический уклон при течении воды.
РЕШЕНИЕ. Запишем уравнение Бернулли для двух сечений потока расположенных в начальной и конечной точках трубопровода.  Здесь: при Z1=0; Z=H=l2sin=70*sin60=60.6 м Т.к. трубопровод постоянного сечения, то согласно уравнению неразрывности F1V1= F2V2; V1= V2, т.е. скорость жидкости во всех сечениях трубопровода одинакова. С учетом выше сказанного, уравнение примет вид:  откуда определяются потери напора между сечениями 1 и 2  где g==10000 Н/м3 – удельный вес воды Гидравлический уклон  Пример № 7. По трубопроводу изображенному на рис., состоящему из 2-х участков стальных, сварных, с незначительной коррозией труб с внутренними диаметрами d1=23 мм и d2=67 мм и длиной l1=70 м и l2=10 м, подается вода в открытый резервуар, где поддерживается постоянный уровень воды над осью входной трубы H=2.5 м. Расход воды Q = 0.002 м3/с Кинематическая вязкость = 1,14*10-4 м2/с. Конец второго участка расположен на h=7 м выше начала трубопровода. Определить избыточное давление в начале трубопровода.
РЕШЕНИЕ. Запишем уравнение Бернулли для сечений взятых в начале и конце трубопровода при Z1=0; Z=h – геометрические напоры.  - пьезометрический напор во втором сечении, тогда здесь V1 и V2 – средние скорости жидкости в соответствующих сечениях.На уравнения расхода:   ; h1-2 – полные потери напора между сечениями. h1-2= hлп+hмп Линейные потери в первом участке:  Для определения коэффициента гидравлических сопротивлений определим режим движения жидкости на этом участке  - режим турбулентграницы зон  ;  здесь = 0,15 мм – эквивалентная шероховатость [1] стр. 99 табл. 9. Re>  имеем квадратичную зону.Для определения  Тогда  Линейные потери 2-го участка   - режим турбулентный.границы зон  ;  т.е.   Для определения используем формулу Альтшуля  Тогда  Общие линейные потери напора h1-2=109.7+0.068=109.77 м. Сумма местных потерь напора  Где: коэффициенты местных сопротивлений: =1+2+3+4. 1=2=0,5 стр. 117 для нового закругленного колена =90о 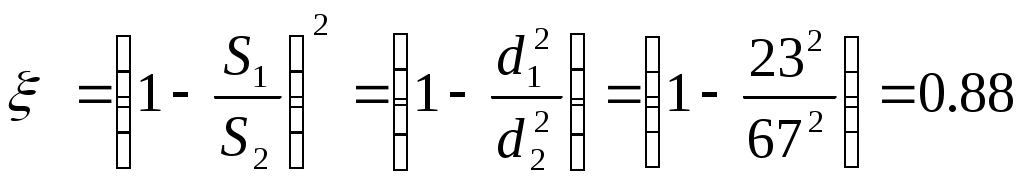 для врезанного расширения трубы [1] стр. 116.4=1 – вход в резервуар [1] стр. 116 = 0,5*0,88*0,5*1=2,88 м  полные потери напора: h1-2=109.77+0.048=109.82 м Избыточное давление в начале трубопровода  Пример № 8. Из открытого резервуара насосом откачивается вода. Расход воды Q=0.12 м3/с. Высота всасывания H=4 м. Диаметр всасывающей линии d=100 мм, длина l=5 м. Трубы стальные, новые. Определить вакуум Рвак на входе насоса.
РЕШЕНИЕ. Вакуум на воде насоса это разность между атмосферным давлением Ра и избыточным давлением в сечении 2 Р2. здесь Z1=0; Z=H; Р1=Р2. V1=0 – скорость понижения уровня жидкости в резервуаре во много раз меньше скорости движения жидкости в трубе (V2).Уравнение принимает вид.  Или  Откуда  Скорость жидкости в трубах  Режим движения жидкости  - турбулентныйграницы зон  ;  здесь – эквивалентная шероховатость новых стальных цельнотянутых труб =0,020,1 [1] стр. 99. коэффициент линейных гидравлических сопротивлений  Сумма коэффициентов местных сопротивлений =к+н. Где к=5010; принимаем к=8 – коэффициент входа во всасывающую коробку с обратными клапанами; н=1,251,5; принимаем п=1,35 – коэффициент резкого поворота без закрепления на 90о = 8+1,35=9,35 Полные потери напора: h1-2= hлп+hмп где: линейные потери напора  местные потери напора   Вакуум на входе в насос  Задачи контрольной работы. № 1. В закрытом сосуде находится жидкость удельного веса . Определить величину давления воздуха, в сосуде над жидкостью, если в трубке двухжидкостного манометра : разность уровней ртути h2 , высота столба воды h1 , разность уровней жидкости в сосуде и ртути в правом колене трубки h3 .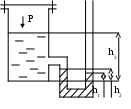 
При решении задачи принять: плотность воды в=1000 кг/м3. Плотность ртути рт =13650 кг/м3. № | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
