Контрольные работы Приложение к ПМ 02. Пм 02. Эксплуатация нефтегазопромыслового оборудования
 Скачать 2.3 Mb.
|
Задачи 11 –20Перед началом решения задач этой группы изучить тему 1.8. Особое внимание следует уделить i- S (h- S) диаграмме водяного пара и изображения, в этой диаграмме простейших процессов i - S диаграмма водяного пара приведена в приложении 3. При работе с i - S диаграммой следует помнить, что изобары и изотермы сливаются в области влажного насыщенного пара (т.е ниже линии х = 1 ), а в области перегретого пара (выше линии х = 1) расходятся. Точки, характеризующие состояние сухого насыщенного пара располагаются на линии х = 1. Задачи 21-30При решении задач следует учесть, что в данном случае нельзя воспользоваться уравнением состояния идеального газа. Следует учитывать общеизвестные понятия. Плотность  = М/V ( кг/м3)Удельный объем v = V/М (м3/кг)  Нужно помнить, что адиабатный процесс также называется изоэнтропийным, т.е энтропия в адиабатном процессе не изменяется ( S=O) Решение задачи проиллюстрируйте схемой, т.е. выкопировкой из i- S диаграммы. Рассмотрите примеры 3 и 4. Для успешного решения этих задач следует изучить темы 1.6. и 1.12. Рассматривая предложенный в задаче теоретический цикл, следует схематично начертить его P - v диаграмму и четко уяснить из каких элементарных процессов он складывается, в каких процессах происходит подвод и отвод тепла. При определении параметров состояния в характерных точках цикла следует использовать уравнение состояния: P*v = R*T, если для данной точки уже известны или ранее определены 2 каких то параметра, или соотношениями между параметрами в процессах. При вычислении подведенного тепла, следует внимательно определить, в каком термодинамическом процессе оно подводится; Например: подведенное тепло. В изобарном процессе q1=Cp* (T2 - T1); В изохорном процессе q 1 =Cv* (T 2 - T 1 ) В изотермическом q1 =2 .3* R*T* 1g (U 2/U 1 ) Величина, полученной в цикле работы и К.П.Д цикла вычисляются по общеизвестным зависимостям. Рассмотрите пример №5. Задачи 31-40Перед началом решения задач этой группы следует изучить темы 2.1.,2.2.,2.3.,2.5. В результате изучения следует четко усвоить основные понятия : тепловой поток, плотность теплового потока или удельный тепловой поток, термическое сопротивление. Следует также понять основные законы теплопроводности и теплоотдачи. Перед решением задач своего варианта рассмотрите примеры 6,7.8 Задачи 41-50Перед решением задач этой группы следует изучить тему 3.1.. При изучении следует хорошо понять количественное отличие элементарного состава топлива в расчете на сухую, горючую и рабочую массу.Следует помнить, что определение теплоты сгорания и расхода кислорода и воздуха необходимого для сжигания топлива, производится по его рабочей массе. Для пересчета одной массы в другую используются соотношения для коэффициентов пересчета.
Примеры решения задач Пример №1 0,5 м3 сернистого газа (SO2) при начальном давлении 0,2 МПа и начальной температуре 27oС, адиабатно сжимается до давления 2 Мпа. Считая зависимость теплоемкости от температуры линейной, определить конечную температуру, конечный объем, изменение внутренней энергии газа и работу затраченную на сжатие. Д  ано: V1= 0,5 м3Р1 = 0.2 Мпа t1 =27 C P2 = 2 Мпа Газ- S02  T2- ?; V2 - ?U- ? L- ? Решение: 1.Определяем удельную газовую постоянную серниcтого газа (SO2)  2.Из уравнения состояния идеального газа : P1* V 1= M*R*T1 определяем массу газа участвующего в процессе M=P1*V 1/R*T1=0 .2* 106 * 0 5/129 .9* 300= 2.5 кг. 3.Для адиабатного процесса справедливо соотношение;  Здесь к = 1.3. коэффициент Пуассона для 3-х атомных газов, откуда определяем конечную температуру газа Т2 =Т1*(Р1/ Р2) к -1/к =300* (2 /0.2)1..3-1/1..3.=513 К t2 =513-273= 240 0 C 4. По таблице приложения (1) интерполируя, определяем истинные удельные, изохорные массовые теплоемкости SO2 при t1 = 27 C и t 2= 240 C  ;  5. Определяем среднюю удельную изохорную, массовую теплоемкость сернистого газа в процессе  6.Определяем изменение внутренней энергии в адиабатном ( впрочем как и во всех других элементарных процессах)  U= Cv cp* (T2 - T1)* М= 0.501* (513-300)* 2.5 = 266.78 кДж7. Из соотношения давления и объема в адиабатном процессе (Р1/Р2)=(V2/V1)к ; определяем конечный объем газа : V2 =V1* (Р1/Р2)1/к =0.5*(0.2/2)1/1.3 = 0.0831 м3 ; или для проверки определим конечный объем из уравнения состояния: Р2* V2= М*R*Т2. V2=М*R*T2/Р2=2.5* 129.9* 513 /2*106 =0.0832 м3 Расхождение результатов составляет всего 0.0001,что допустимо. 8.Определим работу, совершенную в процессе: L= (R/K-1)*(T1-T2)* М= (129.9/1.3.-1)* (300-513)*2.5=230572.5 Дж  -230.6 кДж знак (-)в результате, показывает, что работа была затрачена.Ответ:T2=513 K, V2=0.0831 м3, U=266.78 кДж, L=230.6 кДж Пример № 2 Какое количество теплоты необходимо затратить. чтобы нагреть 2 м3 воздуха при постоянном давлении Р=0.2 Мпа от 1000 С до 5000 С?. Какую работу при этом совершит воздух? Теплоемкость воздуха считать постоянной
Пример № 3 Определить энтальпию и энтропию сухого насыщенного газа при температуре 400 0С
 Пример № 4 Водяной пар имеет давление 0.2. Мпа и сухость Х=0.85. Какое количество тепла следует затратить, чтобы 7 кг этого пара нагреть до 800 0 С, при постоянном давлении. Какова при этом будет плотность пара?
Пример № 5 Для идеального цикла поршневого двигателя внутреннего сгорания с подводом тепла при V = const, определить параметры рабочего тела в характерных точках, полученную работу, термический К.П.Д., количество подведенной и отведенной теплоты, если известно: P1= 0.1 MПа, t1=20 С, = 3.6. ,  =3.33Рабочим телом считать воздух. Теплоемкость считать постоянной.
На схеме процессы: 1-2- адиабатное сжатие рабочего тела 2-3- изохорный подвод тепла, 3-4 – адиабатное расширение, 4-1 –изохорный отвод тепла. Расчет ведем для 1 кг. воздуха 1.Определяем параметры состояния в характерных точках Точка 1. Р1 = Мпа; t1=20C- по уловию задачи. Из уравнения состояния P1*V1 = R*T1 определяем удельный объем V1=R* T1/ P1 здесь R=8314/  =8314/29= 287 Дж/кг*к, Т1 =20+273= 293 КU2= 287*293/0.1*106=0.84 кг/м3 Точка 2.Т.к. степень сжатия = V1/V2=3/6,то V2= V1/ =0.84/3.6=0.233 м3/ кг Для адиабатного процесса 1-2 соотношения между температурами и объемами: Т2 /Т1= ( v1 / v 2) К-1; где К- коэффициент Пуассона для 2-х атомных газов ( воздух- это смесь в основном 2-х атомных газов) Откуда температура Т2=Т1* ( v 1 / v2)К-1= 293* (0.84/0.233) 1,4-1= 489 К .t2 = 489.273= 216С Из уравня состояния Р2* V2 =R*T2 определим давление Р2= R*T2/V2=287*489/0.233=600000 Па= 0.6 Мпа Точка 3. Удельный объем v 3 = v2= 0.233 м3/ кг- процесс 2-3 изохорный. Степень повышения давления = P3/ P2 – по определению. Откуда давление Р3= *Р2=3.33*0.6 = 2 МпаДля изохорного процесса 2-3 соотношение между давлениями и температурами: Р3/Р2 =Т3/Т2., откуда Т3 =Т2* Р3/ Р2 =Т2* =489*3.33= 1628 К; t 3=1628 –273=1355 C Точка 4.Удельный объем v4 = v1 =0/84 м3/кг - процесс 4-1 изохорный. В адиабатном процессе 3-4 справедливо соотношение Т4 =Т3* (v 3 / v4) К-1; откуда Т4 =Т3*( v3/ v4) К-1= Т3* ( v2 /v1)К-1 =Т3*(1/) К-1 =1628/3.6 0.4 =976 К В изохорном процессе 4-1 справедливо соотношение Р4/Р1 =Т4 /Т1; откуда Р4=Р1*Т4 /Т1 =0.1*97/6/293=0.33 Мпа 2.Количество подведенного тепла в изохорном процессе 2-3 q1 = Cv*(Т3-Т 2) здесь: Сv – изохорная массовая удельная теплоемкость Сv = R/(K-1)= 287/(1/4-1)= 717.5 Дж/кг*к; q1= 717.5*(1628-489) = 82500 Дж/кг 3.Количество отведенного тепла в изохорном процессе 4-1 q2=Cv*(T 4-T1)=717.5*(976-293)=495000Дж/кг= 495 кДж/кг 4.Работа, полученная в цикле:  = q 1 –q 2 = 825-495 = 330 Кдж5.К.П.Д. цикла (термический)  q1 =330/825 = 0.4Для проверки определим К.П.Д. по другой формуле:  к-1) = 1- (1/3.61.4.-1)=0.4Пример № 6 Кирпичная стенка имеет толщину 40 см. Одна поверхность стенки имеет температуру 20 С, другая – 20 С. Принимая коэффициент теплопроводности стенки = 0.6 Вт/м* к. Определить плотность теплового потока в стенке и термическое сопротивление стенки.Дано: t1 = 20C t 2 = -20 C  0.6 Вт/м* к 40 см.Решение: Для решения используем закон теплопроводности (Фурье) т.е плотность теплового потока q = * (t 1 –t 2)/ =0.6*(20-(-20))/0.4=60 (Вт/м2)Термическое сопротивление стенки R=  0/667 (м2к/Вт)В качестве проверки определим q=(t1 - t2)/ R = (20 –(20))/0.667=60 ( Вт/м2) м2 к/Вт q- ? R- ? Пример № 7 Поверхность стенки площадью 4 м2 омывается водой с температурой 70 0С. Определить тепловой поток от воды к поверхности стенки, если последняя имеет температуру 680С. Коэффициент теплоотдачи от воды к стенке принять = 90 Вт/м2*к
| |||||||||||||||||||||||||||
-кажущаяся молекулярная масса воздуха.
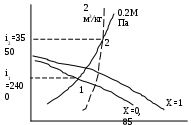ля определения плотности пара в конечном состоянии выясним, какая пунктирная линия проходит через точку 2.Это будет величина удельного объема V= 2м3/кг. Следовательно, плотность пара P= 1/V = ½=0.5. кг/м3
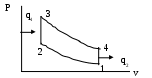Дано:
( t 1 - t 2 )*F=90* (70-68)*4 =720 Вт