Балкулиев стат. По данным таблицы рассчитать поквартально проценты установленного планового задания и проценты выполнения плана по выпуску продукции Расчетные данные оформить в таблице
 Скачать 86.64 Kb.
|
Раздел Общая теория статистики Тема Абсолютные и относительные величины По данным таблицы рассчитать поквартально проценты установленного планового задания и проценты выполнения плана по выпуску продукции; Расчетные данные оформить в таблице.
Вычислим показатели выполнения плана за соответствующий квартал: Процент выполнения плана = (фактический выпуск продукции/ плановый выпуск продукции) x100% По расчетам можно сделать следующие выводы: более высокий процент перевыполнения плана по выпуску продукции приходится на II квартал (110,6%). В III квартале план был перевыполнен лишь на 4,3% (104,3 - 100). Относительные величины планового задания - показатели, характеризующие степень установления планового задания на отчетный период. Рассчитываются по формуле: Процент планового задания = (плановые данные на отчетный период/Фактические данные за базисный период) x100% По расчетам можно сделать следующие выводы: более высокий процент установления планового задания приходится на III квартал - 102,7%, в то время как на I квартал всего лишь 100,1%, на II квартал - 100,2%, на IV квартал - 100,4%. Тема Средние величины По данным таблицы рассчитать средний стаж работника
Средний стаж работника составит: (2,5x18+7,5x40+12,5x15+17,5x10)/83=8,5 года Тема Показатели динамики По данным выпуска товарной продукции рассчитать аналитические показатели динамики и заполнить таблицу
Абсолютный прирост (Л) определяется как разность между отчетным и предыдущим уровнями ряда динамики, т.е. по формуле Δ= уi – yi-1, где уi - уровни ряда динамики (численные значения ряда динамики). Абсолютный прирост характеризует абсолютное изменение явления в отчетном периоде по сравнению с предыдущим. Например, абсолютный прирост продукции в феврале по сравнению с январем составил Δ 2=244 - 236=8 тыс.руб., а в марте по сравнению с февралем Δ 3=246 - 244=2 тыс.руб. и т.п. Результаты расчетов сведены в таблице. Как видно из расчетных данных, наиболее значительно возрос объем продукции в феврале - на 8 тыс. руб., в то время как в мае абсолютный прирост продукции составил всего 1 тыс. руб. Средний абсолютный прирост (Δ) определяется на основе данных абсолютных приростов по следующим формулам: Δ=ΣΔ/n-1 или (yn-y1)/n-1, где п - число уровней ряда динамики; У1 и Уп - соответственно первый и последний абсолютные уровни ряда динамики. Средний абсолютный прирост за рассматриваемый период динамики составит: Δ=(8 + 2 + 3 +1 + 2)/(6-1)=3.2 тыс.руб Δ=(252-236)/(6-1)=3.2 тыс.руб Таким образом, за рассматриваемый период прирост продукции в среднем составил 3,2 млн. руб. Темп роста (Тр) определяется по формуле: Tp = (y1/y0)x100%, где у0 - уровень ряда динамики, взятый за базу сравнения. Темп роста характеризует относительный рост явления за рассматриваемый период. Темпы роста рассчитываются по принципу цепных и базисных соотношений. В том случае, когда за базу сравнения принимается предыдущий период, рассчитываются цепные показатели темпа роста; когда сравнение осуществляется с любым другим уровнем ряда динамики, взятым за базу сравнения, рассчитываются базисные темпы роста. Так, в феврале по сравнению с январем выпуск продукции составил Тр2 = (244:236)-100% = 103,4%, а в марте по сравнению с февралем Тр3 = (246:244)-100% = 100,8% и т.п. Результаты расчетов цепных темпов роста см. в табл. Как видно, наиболее значительно возрос объем продукции в феврале (Тр2 = 103,4%), менее всего увеличился объем продукции в мае (Тр5 = 100,4%). Если за базу сравнения взять январь, то выпуск продукции в марте по сравнению с январем составил Тр3 = 104,3%, а в апреле по сравнению с январем - 105,5% и т.п. Результаты расчетов базисных темпов роста сведем в табл. 1. Как видно из расчетных данных, базисные показатели темпов роста резко отличаются от цепных. Так, в июне по сравнению с маем темп роста выпуска продукции составил 100,8%, а по сравнению с январем - 106,8%. Аналогичные сравнения можно провести и по другим месяцам. Темп прироста (Тпр) характеризует относительный прирост явления за рассматриваемый период. Темп прироста определяется по формуле: Тпр = Тр - 100%. Так же, как и темпы роста, темпы прироста бывают цепные и базисные. Цепные темпы прироста составят: в феврале - Тпр2 = 3,4% (103,4 - 100), в марте - Тпр3 = 0,8% (100,8 - 100) и т.п. Базисные темпы прироста составят: в феврале - Тпр2 = 3,4% (103,4-100), в марте - Тпр3 = 4,2% (104,2 - 100) и в апреле Тпр4 = 5,5% (105,5 - 100) и т.п. Из расчетных значений цепных темпов прироста ясно, что наиболее значительно увеличился объем выпуска продукции в феврале - на 3,4% (103,4 - 100), а менее всего - в мае - на 0,4% (100,4-100). Базисный темп роста за июнь характеризует увеличение объема выпуска продукции за первое полугодие на 6,8% (106,8 - 100). Абсолютное значение одного процента прироста (А) характеризует абсолютный эквивалент одного процента прироста и определяется по формуле: A = Δ/Tпр. Так, в феврале абсолютное значение одного процента прироста составило А2 = (8:3,4) = 2,4 млн. руб.; в марте - А3 = (2:0,8) = 2,5 млн. руб. и т.п. Средний темп роста (Х) за период динамики определяют по формуле средней геометрической на основе данных цепных коэффициентов динамики либо на основе данных абсолютных уровней ряда динамики по формулам: 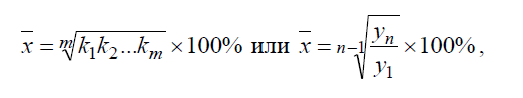 где ki,k2,...km - коэффициенты динамики по отношению к предыдущему периоду; m - число коэффициентов динамики; n - число абсолютных уровней ряда динамики; у1 и yn - соответственно первый и последний абсолютные уровни ряда динамики. За первое полугодие средний годовой темп роста продукции составил 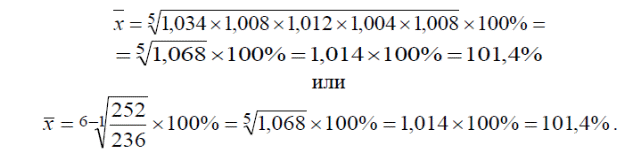 ,Таким образом, за рассматриваемый период объем выпуска продукции возрос в среднем на 1,4%. Тема Индексы По данным таблицы рассчитать сводные индексы стоимостного объема продукции, физического объема продукции и цен. Исходные данные
Рассчитаем индивидуальные индексы продукции и индивидуальные индексы цен. Индивидуальные индексы по соответствующим видам продукции составят: iq(А) =q1/q0 = (4452/4402) x100% =101,1% iq(Б) =q1/q0 = (1150/1248) x100% =92,1% , т.е. в отчетном периоде по сравнению с базисным произведено продукции вида А на 1,1% (101,1 – 100) больше, а вида Б на 7,9% меньше (92,1 – 100). Индивидуальные индексы цен по соответствующим видам продукции составят: ip(А) =P1/P0=(0.5/0.6) x100 = 83,3% ip(Б) =P1/P0=(0.8/1.2) x100 =66,7%, т.е. цена единицы продукции вида А в отчетном периоде по сравнению с базисным снизилась на 16,7% (83,3 – 100), вида Б снизилась на 33,3% (66,7 – 100). Индивидуальные индексы конкретного вида продукции в стоимостном выражении, соответственно, составят: iqp(А) 100% 84,3% iqp(Б) 100% 61,4% Таким образом, объем продукции в стоимостном выражении вида А в отчетном периоде по сравнению с базисным снизился на 15,7% (84,3-100), вида Б –на 38,6% (61,4 – 100). Для того чтобы ответить на вопрос, как изменился объем всей продукции предприятия в отчетном периоде по сравнению с базисным, необходимо рассчитать сводные индексы продукции, цен и физического объема продукции. Сводный индекс объема продукции в стоимостном выражении составит: Iqp= Σq1p1/ Σq0p0 =((4452x0.5+1150.8)/(4402x0.6+1248x1.2))x100%=76% Сводный индекс цен составит: I p= Σq1p1/ Σq1p0 =((4452x0.5+1150.8)/(4402x0.6+1150x1.2))x100%=77.7% Сводный индекс объема продукции составит: Iq Σq1p0/ Σq0p0 =((4452x0.6+1150.8)/(4402x0.6+1248x1.2))x100%=97.9% Используя первое свойство индексов, имеем: Iqp = Iq·Ip; 76%=0,777x0,979x100%. Используя второе свойство индексов, имеем: Δqp(qp) =Δqp(q)+ Δqp(p), т.е. (3146 – 4138,8) = (4051,2 – 4138,8) + (3146 – 4051,2) или –992,8 = –87,6 – 905,2. Таким образом, можно сделать вывод: объем продукции в стоимостном выражении уменьшился в целом на 24% (76,0 – 100), или на 992,8 тыс. руб. (3146 – 4138,8); в том числе за счет снижения цен на 22,3 % (77,7 – 100) объем продукции в стоимостном отношении выражении снизился на 905,2 тыс. руб. (3146 – 4051,2) и за счет снижения физического объема продукции на 2,1 % (97,9- 100) объем продукции в стоимостном выражении уменьшился на 87,6 тыс. руб. (4051,2 – 4138,8). Тема Графическое изображение статистических данных По данным таблицы построить графики динамики в виде линейной и столбиковой диаграмм
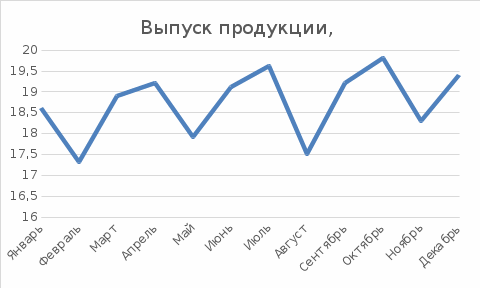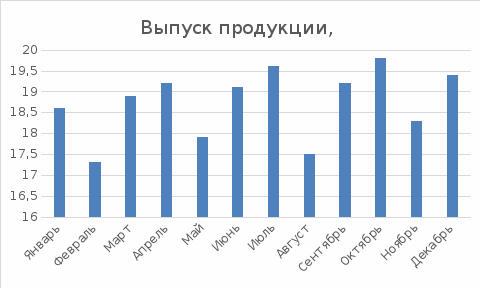  Тема Взаимосвязи экономических явлений По данным таблицы построить аналитическое уравнение зависимости разряда рабочих от стажа работы. С помощью линейного коэффициента корреляции определить тесноту связи между явлениями.
Определим форму зависимости разряда рабочих от стажа их работы на предприятии, используя графический метод (рис. 10.1). Судя по распределению, зависимость прямолинейная. Как известно, прямолинейная зависимость подчиняется уравнению прямой:  .Следовательно, параметры данного уравнения связи находятся путем решения следующей системы уравнений: 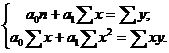 Для решения системы построим вспомогательную таблицу:
* В ранжированном порядке (в порядке возрастания значений х). На основе данных таблицы имеем систему уравнений в следующем виде: 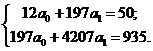 Решим систему сравнений: 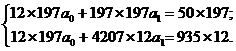 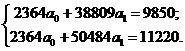 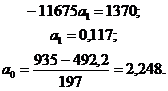 Следовательно, найденное аналитическое уравнение связи имеет вид:  подставим соответствующие значения х в уравнение и найдем новые значения  .Изобразим по найденным значениям теоретическую линию регрессии, которая, как видно, с некоторыми погрешностями воспроизводит эмпирическую линию регрессии. Так как  , то можно считать, что построенное парное уравнение корреляции является искомым, и мы вправе сделать следующий вывод: с увеличением стажа работы на один год разряд рабочих в среднем возрастает на 0,117.Как было ранее сказано, экономическая интерпретация аналитического уравнения связи может осуществляться с помощью коэффициента эластичности. Расчетная величина коэффициента эластичности:  Таким образом, увеличение стажа работы на 1 процент приводит к увеличению разряда на 0,456 процента. Как было сказано ранее, для установления тесноты связи между факторным и результативным признаками в случае линейной зависимости применяется линейный коэффициент корреляции. Рассчитываем величину линейного коэффициента корреляции:        Как видно, связь между разрядом рабочего и стажем его работы на предприятии достаточно значительная, так как r = 0,77 близко к «1». Для установления размера вариации разряда рабочего от стажа его работы рассчитываем коэффициент детерминации:  Следовательно, на 59,3% вариация разряда рабочего объясняется изменением стажа его работы на предприятии. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||