ответы мат методы (1). По предмету математические методы
 Скачать 426 Kb.
|
|
6. Методы решения многокритер-х задач. Парето - Пусть в составе множ-ва возможных решений есть два решения х1и х2 такие, что все критерии W1, W2,…, Wк для первого реш-я больше или равны соответствующим критериям для второго реш-я, причем хотя бы один из них действит-но больше. Очевидно что в составе множества Х нет смысла сохранять решение х2, оно вытесняется решением х1. Выбросим решение х2, как не конкурентно спос-е и перейдем к сравнению других по всем критериям. В результате отбрасыв-ся не выгодные решения, множество Х сильно уменьшается. В нем сохраняются только эффективные(паретовские) реш-я. Линейная свертка – здесь участвуют человек и ПК. Указывается вес события:а1,а2,…,а3.Машина производит расчеты и выдает показатели эффективности(как бы в ряд): W1, W2… Wn, а человек может критически оценить ситуацию и внести измен-я в весовые коэфф-ты(или иные параметры управляющего алгоритма). В конечном итоге решение все равно принимает человек. наложение ограничений на показ-ли эффективности – надо выделить один(главный) показатель W1 и стремиться его обратить в максимум, а на все остальные W2, W3, ....( чтобы прибыль была максим-я, план по ассортименту выполнен, а себестоимость прод-и не выше заданной). При таком подходе все показ-ли, кроме одного – главного перев-ся в разряд заданных условий а(альфа). метод последовательных уступок – Предположим что показатели W1, W2… Wn, расположены в порядке убывающей важности. Сначала ищется решение, обращающее в максимум первый(важнейший) показатель W1= W1*. Затем назначается, исходя из практических соображений, с учетом малой точности, с которой нам известны входные данные, некоторая уступка и ΔW1, которую мы согласны сделать для того чтобы максим-вать второй показатель W2. Наложим на показатель W1 ограничение: чтобы он был меньше, чем W1*- ΔW1, и при этом ограничении ищем решение, обращающее в максимум W2. Далее снова назначаем уступку в W2, ценой которой можно максимизировать W3, и т.д. Такой способ построения компромиссного хорош тем, что здесь сразу видно, ценой какой уступки, в одном показателе приобретается выигрыш в другом и какова величина этого выигрыша. 8. Осн-я задача лин-го программир-я (ОЗЛП) и сведение произв-й задачи лин-го программир-я к осн-й задаче лин-го прогр-я. Любую задачу ЛП можно свести к стандарт.форме (ОЗЛП), ктр формулир-ся так: найти неотриц.знач-я переменных х1, х2, …, хn, ктр удовлетворяли бы условиям-рав-вам 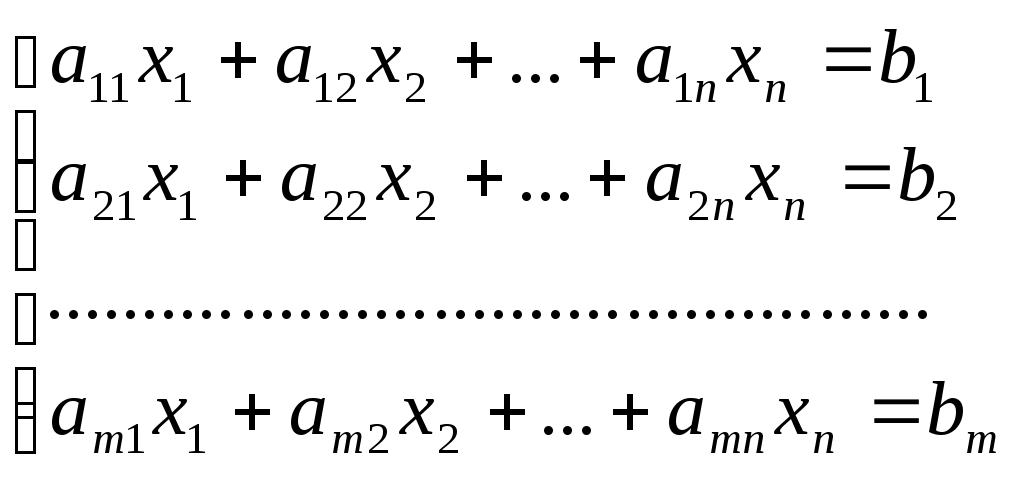 и обращали бы в мах лин.f-ю этих переменных:  . Назовем допустимым решением ОЗЛП всякую совок-ть неотриц.знач-й х1, х2, …, хn, удовлетворяющую условиям системы. Оптимальным назовем то из допустимых решений, ктр обращает в мах f-ю L. Требуется найти оптим.решение. Задачи ЛП сводятся к ОЗЛП, где необх-мо найти неотриц.знач-я пер-ных х1, х2, …, хn, удовлетворяющие сис-ме m-лин.нерав-в и ур-й, и обращающие в max (min) лин.f-ю этих пер-ных. F=c1x1+c2x2+…+cnxn→max (min). Назовем допустимым решением ОЗЛП всякую совок-ть неотриц.знач-й х1, х2, …, хn, удовлетвор.сис-ме огранич-й. Оптимальным назовем то из допустим.реш-й, ктр обращает в max(min) цел.f-ю. Рассмотрим задачу ЛП с 2мя пер-ными (n=2). Пусть геом.изображ-ем сис-мы огранич-й явл-ся многоуг-к. Необх-мо среди точек этого мног-ка найти такую точку (вершину), в ктр лин.f-я принимает max (min) знач-е. Рассмотрим так наз-мую линию уровня лин.f-и F, т.е. линию, вдоль ктр эта f-я принимает одно и тоже фиксирован.знач-е а, т.е. с1х1+с2х2=а. На мног-ке реш-й следует найти точку, через ктр проходит линия уровня f-и F с наибольшим (если f-я max-ется) или наим.(если f-я min-ется) уровнем. Ур-е линии уровня f-и есть ур-е прямой линии. При различ.уровнях а линии уровня //, т.к. их угловые коэф-ты опр-ся только соотнош-ем между коэф-тами с1 и с2, и след-но, =. Т.о., линии уровня f-и F – это своеобразные параллели, расположенные обычно под углом к осям корд-т. Важн.св-во линии уровня лин.f-и состоит в том, что при // смещении линии в одну сторону уровень только возрастает, а при смещ-и в др.сторону – только убывает. 9. Симплекс–метод при решении ОЗЛП. Симплекс-метод явл-ся одним из способов решения ЗЛП. Идея последоват.улучшения решения легла в основу универсал.метода решения ЗЛП – с-м. Геометрич.смысл с-м состоит в последоват.переходе от одной вершины (первоначальной) многогранника огранич-й к соседней, в ктр лин.f-я принимает лучшее (не худшее) знач-е (по отношению к цели задачи) до тех пор, пока не будет найдено оптим.реш-е – вершина, где достиг-ся оптим.знач-е f-и цели (если задача имеет конечный оптимум). С-м – это вычислит.процедура, основанная на принципе последоват.улучшения решений при переходе от одной базисной точки (базисного решения) к др. При этом знач-е цел.f-и улучшается. Базисным реш-ем явл-ся одно из допустимых реш-й, нах-щихся в вершинах области допустимых знач-й. Проверяя на оптим-ть вершину за вершиной симплекса, приходят к искомому оптимуму. На этом принципе основан с-м. С-м может быть найден на мах и min. 1.MAX. (Задача об использ-и ресурсов): имеются 2вида продукции P1 и P2, использ-ся 4вида ресурсов S1, S2, S3, S4. Необх-мо составить такой план произв-ва продукции, при ктр прибыль от ее реализации будет мах. 1)Необх-мо из сис-мы огранич-й, ктр выглядит в виде сис-мы нерав-в, сделать сис-му ур-ий (если «», то осн.пер-ные со знаком +, если «», то -). Д/этого придется ввести дополнит.неотриц.переменные. Опр-м, какие из переменных явл-ся осн., а какие – неосн. Пр-ло: в кач-ве осн.пер-ных на I шаге следует выбрать (если возможно) такие m-пер-ных, каждая из ктр входит только в 1 из m-ур-ий сис-мы огранич-й, при этом нет таких ур-ий сис-мы, в ктр не входит ни одна из этих пер-ных. Далее выражаем осн.пер-ные через неосн. Положив, неосн.пер-ные = 0, получим I базисное реш-е. 2)Составим сим.таблицу: а)исх.расширен.сис-му (в ктр выражали осн.пер-ные через неосн.) заносим в I сим.таблицу. Послед.строка таблицы, в ктр приведено ур-ие д/лин.f-и цели, наз-ся оценочной. В ней указыв-ся коэф-ты цел.f-и с противополож.знаком. В лев.столбце таблицы записываем осн.пер-ные (базис), в I строке таблицы – все пер-ные (отмечая при этом осн.), во II столбце – свобод.члены расширен.сис-мы  . Последний столбец – д/оц.отнош-й, необх-мых при расчете наибольшего знач-я пер-ной. В рабоч.часть таблицы занесены коэф-ты  при пер-ных из расширен.сис-мы. Далее таблица преобраз-ся по опр.правилам. б)Проверяем выполн-е критерия оптим-ти. При реш-и задачи на мах – наличие в послед.строке отриц.коэф-тов. Если таких коэф-тов нет, то реш-е оптимально, т.е. достигнут мах. При этом  , осн.пер-ные принимают значение  (II столбец). Осн.пер-ные = 0, т.е. получено оптим.реш-е. Иначе, переходим к след.шагу. в)Если критерий оптим-ти не выполнен, то наибольший по модулю отриц.коэф-т в послед.строке таблицы опр-ет разрешающий столбец S. Составляем оц.отнош-я кажд.строки по след.правилам: а)  если  и  имеют разные знаки; б) и  ; в) ; г)0, если и  ; д) , если и имеют одинак.знаки. Опр-ем min . Если конечного min нет, то задача не имеет конечного оптимума, т.е.  . Если min конечен, то выбираем строку q, на ктр он достиг-ся (если их неск-ко, то выбираем любую) и назовем ее разрешающей строкой. На пересечении разреш.столбца и разреш.строки нах-ся разрешающий элемент . г)Переходим к след.таблице по след.правилам: а)в лев.столбце записываем новый базис: вместо осн.пер-ных хq записываем хs; б)в столбцах, соотв-щих осн.пер-ным, проставляем: 1 – против «своей» осн.пер-ной, 0 – против «чужой» осн.пер-ной, 0 – в послед.строке д/всех осн.пер-ных; в)нов.строку с № q получаем из старой строки делением на разреш.столбец ;г)все остальные пер-ные пересчитываем по правилу прямоугольника. Далее переходим к пункту 2.2.MIN. Сначала также преобраз-ся сис-ма нерав-в в сис-му ур-ий, выражаем осн.пер-ные через неосн. Критерий оптим-ти при отыскании min лин.f-и: если в выраж-и лин.f-и через неосн.пер-ные отсутствуют отриц.коэф-ты при неосн.пер-ных, то реш-е оптимально. Смотрим, есть ли в итог.столбце (свобод.членов) отриц.знаки. Если да, то это явл-ся свидетельством того, что дан.план нельзя считать допустимым. Ликвидация отриц.чисел в итог.столбце начин-ся с наибольшего по абсолют.величине (это будет ключевая строка). Найдем ключ.столбец. Д/этого нужно эл-ты цел.строки разделить на эл-ты ключ.строки (оц.отнош-я) д/столбцов. Из получен.отнош-й выбираем наименьшее. На пересеч-и ключ.строки и столбца нах-ся ключ.эл-т. Далее все происходит также. 10. Транспортная задача. # Имеется m пунктов отправления (пунктов произв-ва) Аi …, Аm, в ктр сосредоточены запасы однород.продуктов в кол-ве a1, ..., аm ед-ц. Имеется n пунктов назнач-я (пунктов потребления) В1, ..., Вn, потреб-ть ктр в указанных продуктах составляет b1, ..., bn ед-ц. Известны также транспорт.расходы Сij, связанные с перевозкой ед-цы продукта из пункта Ai в пункт Вj, (i  1, …, m; j 1, ..., n). Постановка задачи: Найти V перевозок д/кажд.пары «поставщ.-потреб.» так, чтобы: 1)мощ-ти всех пост-ков были реализованы; 2)спросы всех потреб-лей были удовлетворены; 3)затраты на перевозку были min. Особен-ти эк.-мат.модели ТЗ: 1)сис-мы огранич-й – есть сис-мы ур-ий; 2)коэф-ты при неизвестных в сис-мах огранич-й = 1 или 0; 3)кажд.переменная входит в сис-му огранич-й 2раза – 1раз в I сис-му и 1раз во II. Всякое неотриц.реш-е сис-мы лин.ур-й, опр-мое матрицей X=(xij) (i=1, …, m; j=1, ..., n), наз-ся планом ТЗ. План X=(xij)(i=1, …, m; j=1, ..., n), при ктр f-я принимает свое min значение, наз-ся оптимал.планом ТЗ. Если мощ-ть всех пост-ков=сум.мощ-ти потреб-лей, то такие задачи наз-ся закрытыми, в против.случае – открытого типа. Т: число r осн.(базисных) переменных закрытой ТЗ = m+n-1 (m-число пост-ков, n-потреб-лей). Кажд.разбиению переменных xij задачи на осн.(базисные) и неосн.(свобод.) соотв-ет базис.реш-е и, как следствие, заполнение таблицы поставок, ктр также наз-ся базисным. Др.словами, распред-е поставок наз-ся базисным, если переменные, соотв-щие заполненным клеткам, можно принять за осн.переменные. Клетки, отвечающие базис.переменным, наз-ся базисными, а клетки, соотв-щие свобод.перемен., свободными или пустыми. 11. Методы нахож-я начал-го реш-я трансп-й з-чи. Д/начала нахождения оптимал.решения требуется найти исх.базисное распред-е поставок – опорный план. Рассмотрим метод «сев.-запад.угла» д/нахожд-я опор.плана. Переносим все коэф-ты из ур-й в таблицу – опорное реш-е выполнено. При этом цел.f-я принимает знач-е суммы произведений верх.угла клетки на нижний угол. Надо, чтобы число заполненных клеток было = m (мощ-ть пост-ков) + n (спрос потреб-лей) - 1. Недостаток этого метода в том, что он построен без учета знач-й коэф-тов затрат задачи. С др.стороны дан.метод допускает модификацию, лишенную этого недостатка, т.е. на кажд.шаге max-возможную поставку следует давать не в сев.-запад.клетку оставшейся таблицы, а в клетку с наим.коэф-том затрат. При этом распред-е поставок оказыв-ся ближе к оптимуму, чем распред-е, полученное методом сев.-запад.угла. Метод минимального элемента. Суть метода заключается в том, что из всей таблицы стоимостей выбирают наименьшую и в клетку, которая ей соответствует, помещают меньшее из чисел. Затем из рассмотрения исключают либо строку, соответствующую поставщику, запасы которого полностью израсходованы, либо столбец, соответствующий потребителю, потребности которого полностью удовлетворены, либо и строку и столбец, если израсходованы запасы поставщика и удовлетворены потребности потребителя. Из оставшейся части таблицы стоимостей снова выбирают наименьшую стоимость, и процесс распределения запасов продолжают, пока все запасы не будут распределены, а потребности удовлетворены. 12. Метод потенц-в в решении трансп-й задачи. Необх-мо сделать оценку свобод.клеток. Сущ-ть метода потенциалов состоит в том, что д/кажд.строки и кажд.столбца таблицы опр-ют спец.числа, называемые потенциалами. С помощью них можно установить, нужно ли заполнять свобод.клетку таблицы или ее можно оставить незаполненной. Потенциалы строк и столбцов опр-ся по заполнен.клеткам, нах-щимся на их пересечении. Эл-т заполнен.клетки должен равняться сумме потенциалов строки и столбца, на пересеч-и ктр нах-ся эта заполнен.клетка. Д/начала вычислений I потенциал д/строки или столбца приним-ся условно = 0, а все остальные потенциалы опр-ся с помощью эл-тов заполнен.клеток. Обознач-я: Vj – потенциалы столбцов, Ui – строк, Сij – эл-ты заполнения клеток. Сij = Ui + Vj . После того, как потенциалы столбцов и строк опр-ны, выясняется, явл-ся ли план оптимальным или нет. С этой целью д/кажд.свобод.клетки вычисл-ся сумма потенциалов строк и столбцов, на пересеч-и ктр нах-ся эта клетка. Сравнение суммы потенциалов с величиной эл-та в свобод.клетках позволяет опр-ть, нужно ли заполнять эту клетку или ее нужно оставить свобод. При решении задачи на min (max) не заполн-ся те свобод.клетки, в ктр сумма потенциалов < (>) величины эл-та. Если хар-ка, знач-е ктр = Сij – (Ui + Vj ) положит. (отриц.), то свобод.клетка не заполн-ся при решении задач на min (на max). Свобод.клетки, имеющие нулевое знач-е хар-ки, показывают на то, что их заполнение приведет к перераспред-ю поставок, но объем работ останется неизменным. После этого числа заносим в таблицу и опр-ем связь с неск-кими незаполнен.клетками. Эта связь выявл-ся путем построения замкнутых многоуг-ков, вершинами ктр явл-ся клетки таблицы. Углы в этих многоуг-ках должны быть прямыми. Одна вершина нах-ся в свобод.клетке, а все остальные – в заполнен. Многоуг-к имеет четное кол-во вершин. В этом цикле пересчета + помечены те клетки, поставка в ктр увелич., и «-» – уменьш-ся. Замечание: иногда д/произвол.означенного цикла вводится понятие оценка цикла – алгебраич.сумма коэф-тов, стоящих в вершинах цикла, взятых с соотв-щими знаками. Д/кажд.свобод.клетки базис.распред-я поставок сущ-ет и при том единствен.цикл пересчета. Причем, операция означивания цикла явл-ся корректной. Т.(о потенциалах): оценка свобод.клетки не измен-ся, если к коэф-там затрат некоторой строки (столбца) таблицы поставок прибавить некоторое число. Изменение коэф-тов затрат можно начинать с любого столбца (строки). Потенциал столбца (строки), избранного д/начала, может быть произвольным. Остальные соотв-но необх-мо пересчитывать. 13. Общий вид задач нелинейного программир-я. Графический метод решения задач нелинейного программир-я. Во многих эк.моделях исследов-я операций завис-ти между постоянными и перемен.факторами лишь в I приближ-и можно считать лин., более детальное рассмотр-е позволяет обнаружить их нелин-ть. Как пр-ло, такие показ-ли, как прибыль, с/стоим-ть, капитал.затраты на произв-во и др., в действит-ти зависят от объема произв-ва, расхода ресурсов и т.п. нелинейно. К класс.методам оптимизации относ-ся классы Нелин.задач и др. Задачу оптимизации можно сформулировать так: найти переменные х1…хn, удовлетворяющие сис-ме ур-й  , где i=1,…, m, и обращающие в max (min) целевую f-ю . При этом переменные х1…хn не явл-ся дискретными. F-и и f(х) явл-ся непрерывными и имеют, по кр.мере, частные производные II порядка. #задача Нелин.прогр.: дан.предпр-е д/произв-ва какого-то продукта расходует 2ср-ва в кол-ве х1 и х2. Это факторы произв-ва (машины и труд), 2различных вида сырья… Факторы машины и труд взаимозаменяемы или в с/хоз-ве взаимоз.факторами считаются посевные площади и кол-во удобрений. Vпроизв-ва, выраженный в натурал.или стоим.ед-цах, явл-ся f-ей затрат произв-ва  . Эта завис-ть наз-ся произв-венной f-ей. Издержки зависят от расхода обоих факторов (х1 и х2) и от цен этих факторов (с1 и с2). Совокупные издержки выраж-ся формулой . Требуется при дан.издержках опр-ть такое кол-во факторов произв-ва, ктр max-ет V продукции Z. Мат.модель этой задачи имеет вид: опр-ть такие переменные х1 и х2, удовлетвор-щие усл-ям: 1) ; 2) ; 3)  . Положим, что дважды диф-ма в т. ,  и в некоторой ее окрест-ти. Точка X*, в ктр все частные производные f-и  = 0, наз-ся стационарной точкой. Локал.экстр. Необх.усл-е экстремума. Если в точке х0 f-я имеет экстремум, то . Дост.усл-я экстремума: 1)если х0 – точка max (min), то при переходе через нее  меняет знак с + на – (с – на +). 2)если х0 – точка max (min), то  ( ). 3)если  , то вопрос о сущ-и экстремума остается открытым. Дост.усл-е сущ-я экстремума: 1)если В2-АС<0, то сущ-ет экстремум, причем, если А<0, то х0 – точка max, если А>0, то х0 – точка min. 2)если В2-АС>0, то в точке х0 экстремума нет. 3)если В2-АС=0, то вопрос о сущ-и экстремума остается откр. Глобал.экстр. F-я имеет в точке Х0 заданной обл-ти D глобал.max – наибольшее знач-е в обл-ти D (min – наим.знач.), если нерав-во  ( ) соотв-но выполн-ся д/любой точки X D. Т.(Вейерштрасса): Если обл-ть D замкнута и ограничена, то диф.f-я достигает в этой обл-ти своих наибольшего и наим.знач-й или в стац.точке, или в граничной точке обл-ти. Чтобы найти глобал.экстремум: 1)найти все стац.точки обл-ти D, найти в них знач-я f-и. 2)найти знач-я –и в граничных точках обл-ти D. 3)сравнить эти знач-я и сделать вывод. Услов.экстр. Пусть необх-мо найти экстре- мум f-и при усл-и, что переменные х1…хn удовлетв-ют ур-ям  = 0 (*). Предполаг-ся, что f-и и f(х) имеют непрерыв.част.производные по всем пер-ным, тогда = 0 наз-ют ур-ем связи. Точка  , удовлетворяющей ур-ю *, явл-ся точкой усл.max (min) f-и , если ( ) имеют место д/всех точек X, корд-ты ктр удовлетворяют ур-ям связи. |