ответы мат методы (1). По предмету математические методы
 Скачать 426 Kb.
|
|
14. Метод множителей Лагранжа для решения задач нелинейного программирования. Пусть решается задача опр-я усл.экстремума f-и 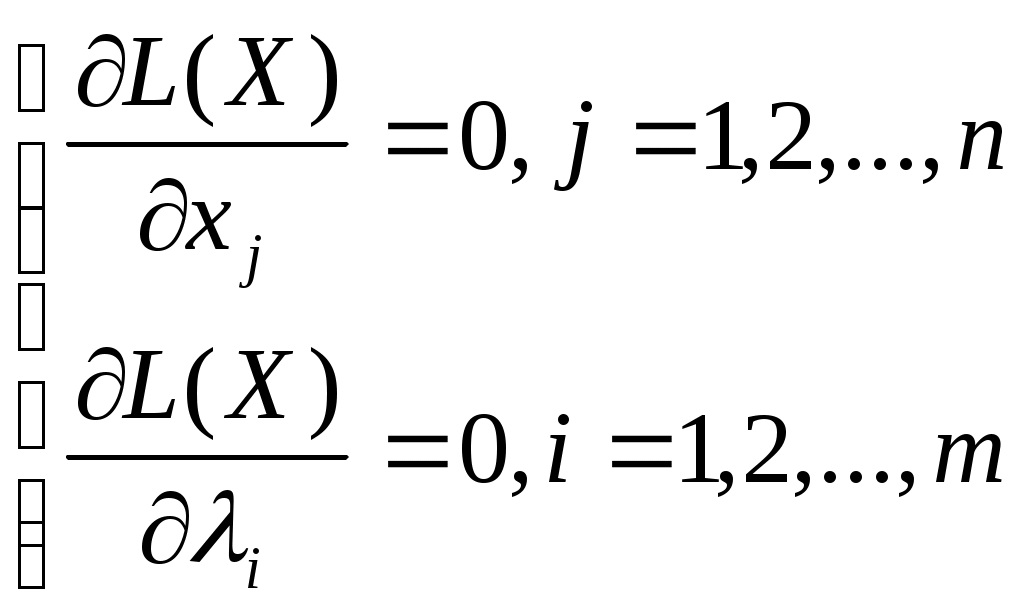 при огранич-ях  =0. Составим f-ю  , ктр наз-ся f-ей Лагранжа.  - постоян.множ-ли (множ-ли Лагранжа). Отметим, что множ-лям Лагранжа можно придать эк.смысл. Если  - доход, соотв-щий этому плану, то - цена (оценка) i-го ресурса, хар-щая изменение экстремального знач-я целевой f-и в завис-ти от изменения размера i-го ресурса (маргинальная оценка). L(X) – f-я n+m переменных ( . Опр-е стац.точек этой f-и приводит к решению сис-мы ур-й:  . Легко заметить, что  , т.е. в это ур-ие входит ур-ие связи. Т.о., задача нахождения усл.экстремума f-и сводится к нахождению локал.экстремума f-и L(X). Если стац.точка найдена, то вопрос о сущ-и экстремума в прост.случаях решается на основании дост.условий экстремума – исследования знака II диф-ла  в стац.точке при условии, что переменные приращения  связаны соотнош-ями:  , i=1,2,m, полученными путем диф-ния ур-ий связи. Для решения примеров, необх-мо найти усл.глобал.экстремум. Ур-ие связи приравнивается к 0. Составл-ся f-ю Лагранжа, нах-ся част.производные этой f-и по  . Приравниваем их к 0 и получаем сис-му. Решая ее, получаем стац.точки, в ктр нах-ся знач-я f-и Z. Выбираем из всех знач-й z наиб.и наим.15. Ос-е понятия динам-го программ-я: шаговое управление, управл-е операцией в целом, оптимальное управление, выигрыш на данном шаге, выигрыш за всю опер-ю, аддитивный критерий. ДП – метод оптимизации, приспособленный к операциям, в ктр процесс принятия решения может быть разбит на шаги. Такие операции наз-ся многошаговыми. Начало развития ДП относ-ся к 50-м годам ХХв. Представим себе некоторую операцию, распадающуюся на ряд послед-ных «шагов» или «этапов» - # деят-ть отрасли пром-ти в течение ряда хоз.лет. Пусть эф-ть операции хар-ся каким-то показ-лем W, ктр для краткости наз-ся «выигрышем». Предположим, что выигрыш за всю операцию складыв-ся из выигрышей на отд.шагах:  , где wi – выигрыш на t-м шаге. Если W обладает таким св-вом, то его наз-ют «аддитивным критерием». Операция, о ктр идет речь, предст-ет собой упр-мый процесс, т.е. мы можем выбирать какие-то пар-ры, влияющие на его ход и исход, причем на кажд.шаге выбир-ся какое-то реш-е, от ктр зависит выигрыш на дан.шаге и выигрыш за операцию в целом. Будем наз-ть это реш-е «шаговым упр-ем». Совок-ть всех шаг.упр-й предст-ет собой упр-е операцией в целом. Обозначим его буквой х, а шаг.упр-я – буквами  : х=( ), где - не числа, а может быть, векторы, f-и. Требуется найти такое упр-е х, при ктр выигрыш обращ-ся в max:  . То упр-е х*, при ктр этот max достиг-ся, наз-ся оптим.упр-ем. Оно состоит из совок-ти оптим.шаг.упр-й: х*=( ). Тот max выигрыш, ктр достиг-ся при этом упр-и, обознач-ся W*: W*=max{W(x)} (величина W* есть max из всех W(x) при разных упр-ях х (max берется по всем упр-ям х, возможным в дан.усл-ях).16. Идея метода динам-го програм-я. Простейшие задачи, решаемые методом дин-го прогр-я. ДП – метод оптимизации, приспособленный к операциям, в ктр процесс принятия решения может быть разбит на шаги. Такие операции наз-ся многошаговыми. Начало развития ДП относ-ся к 50-м годам ХХв. Модели ДП прим-ся при решении задач меньшего масштаба (чем ЛП), #при распред-и дефицитных капитальных вложений между возможными нов.направлениями их использ-я; при составлении календар.планов тек.и капитал.ремонта слож.оборудования и его замены. Эти модели позволяют на основе станд.подхода с использ-ем при min вмешательстве человека принимать такие решения. И если кажд.взятое в отдельности такое реш-е малосущ-но, то в совок-ти эти решения могут оказать большое влияние на прибыль. Планируя многошаг.операцию, надо выбирать упр-е на кажд.шаге с учетом всех его буд.последствий на еще предстоящих шагах. Общ.постановка задач ДП: Рассматр-ся упр-мый процесс, (эк.процесс) распред-я ср-в между предпр-ями, использ-я ресурсов в течение ряда лет, замены оборудов-я, пополнения запасов… В рез-те упр-я сис-ма (объект упр-я) S перевод-ся из начал.состояния s0 в сост-е s . Предположим, что упр-е можно разбить на n шагов, т.е. реш-е приним-ся послед-но на кажд.шаге, а упр-е, переводящее систему S из нач.сост-я в конечное, предст-ет собой совок-ть n пошаговых упр-й. Обозначим через Хк упр-е на k-м шаге (к=1, 2, ..., n). Пер-ные Хк удовлетворяют некоторым огранич-ям и в этом смысле наз-ся допустимыми (Хк может быть числом, точкой в n-мерном простр-ве, кач-ным признаком). Пусть Х(Х1, X2, ..., Хn) – упр-е, переводящее сис-му S из s0 в s . Sk – сост-е сис-мы после к-го шага упр-я. Показ-ль эф-ти рассматриваемой упр-мой операции – цел.f-я - зависит от нач.состояния и упр-я: Z=F(S0;X). Сделаем неск-ко предполож-й: 1)Сост-е Sk сис-мы в конце к-го шага зависит только от предшест.сост-я Sk-1 и упр-я на к-м шаге. Это требов-е наз-ся "отсутствием последействия".  - ур-е сост-й. 2)Цел.f-я явл-ся аддитивной от показ-ля эф-ти кажд.шага. Показ-ль эф-ти кажд.шага:  . Задача пошаг.оптимизации (задача ДП) формулир-ся так: опр-ть такое допустимое упр-е X, переводящее сис-му S из s0 в s , при ктр цел.f-я  принимает наиб.(наим.) знач-е. Особен-ти модели ДП: 1)Задача оптимизации интерпретир-ся как n-шаг.процесс упр-я. 2)Цел.f-я = сумме цел.f-й кажд.шага. 3)Выбор упр-я на k-м шаге зависит только от сост-я сис-мы к этому шагу и не влияет на предшеств.шаги. 4)Сост-е Sk после k-го шага упр-я зависит только от предшеств.сост-я Sk-1 и упр-я Хк (отсутствие последействия). 5)На кажд.шаге упр-е Хк зависит от конеч.числа упр-щих пер-ных, а сост-е Sk - от конеч.числа пар-ров. 17. Опред-е графа и его осн-е характер-ки. Вершины и ребра. Графич-я интерпр-я графа. Смежность и инцидентность. Локальная степень. Подграф. Полный подграф. Пусть А – любое мн-во. Обозначим через V(A) – мн-во всех неупорядоченных пар его различ.эл-тов. #A= {1,2,3}. Тогда V(A)={(1,2);(1,3);(2,3)}. Если мн-во А={1,2}, тогда V(A)={(1,2)}. Если A={1}, тоV(A)=. Когда в записи V(A) указ-ся пара (1,2), то это обозначает одно и то же, что и пара (2,1), т.к. она не упорядоченная. Графом наз-ся пара мн-в Г=[A,B], где А – любое непустое мн-во, ВV(A). Эл-ты из мн-ва А наз-ся вершинами графа, а эл-ты из В – его ребрами. Граф, содержащий только ребра, называется неориентированным; граф, содержащий только дуги – ориентированным или орграфом. Геом. интерпретация графа: пусть Г=[A,B] – некоторый граф. А={a1,a2,…,ap}, В={в1,в2,…,вq}. Фиксируем на плоск-ти проивол.образом р-точек и назовем их А1, А2, …, Ар. Затем д/кажд.пары (аi, аj)В проведем отрезок, соед-щий дан.вершины. Если в некотором графе пара вершин аi, и аj одному ребру, то они наз-ся смежными. В этой ситуации каждый из них наз-ся инцидентной ребру (аi, аj), а ребро (аi, аj) - инцидентно кажд.вершине аi, и аj. Кол-во ребер, инцидентных дан.вершине А, наз-ся ее степенью или локал.степенью графа в вершине А; обознач-е d(a) – степень вершины А. В любом графе кол-во вершин нечетной степени обяз-но четно. Пусть даны Г1=[A1,B1] и Г2=[A2,B2] – два графа таких, что А1А2, а В1В2. Тогда говорят, что граф Г1 явл-ся подграфом Г2. Если в некотором графе Г=[A,B] мн-во ребер В таково, что В=V(A), то дан.граф наз-ся полным. Если в полном графе число вершин р, то ребер будет: (р(р-1)/2). Пусть Г=[A,B] – граф и А={a1,a2,…,ap} – его вершины. Построим квадрат.матрицу, состоящую из эл-тов М=(mij), где i,j=1,2,…,р. 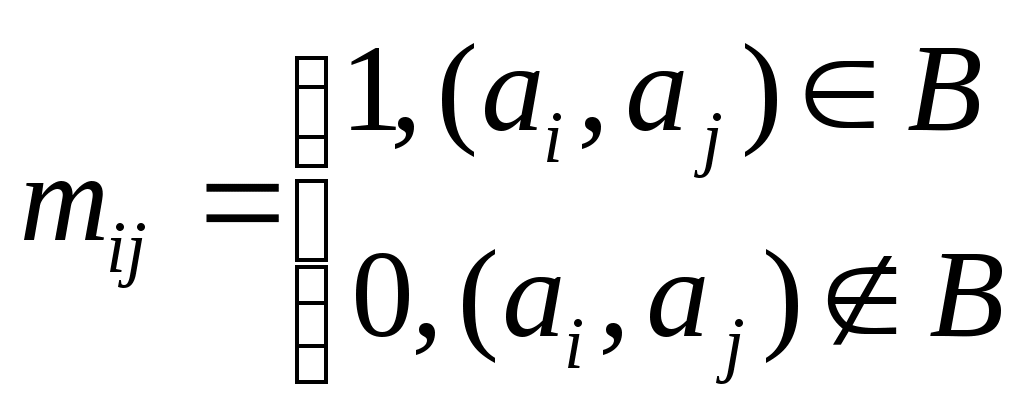 Эта матрица наз-ся матрицей смеж-тей графа. Она симметрична. Сопоставим графу Г=[A,B] еще одну матрицу. А={a1,a2,…,ap} – вершины, В={в1,в2,…,вq} – ребра. Определим матрицу N=(nij) след.образом: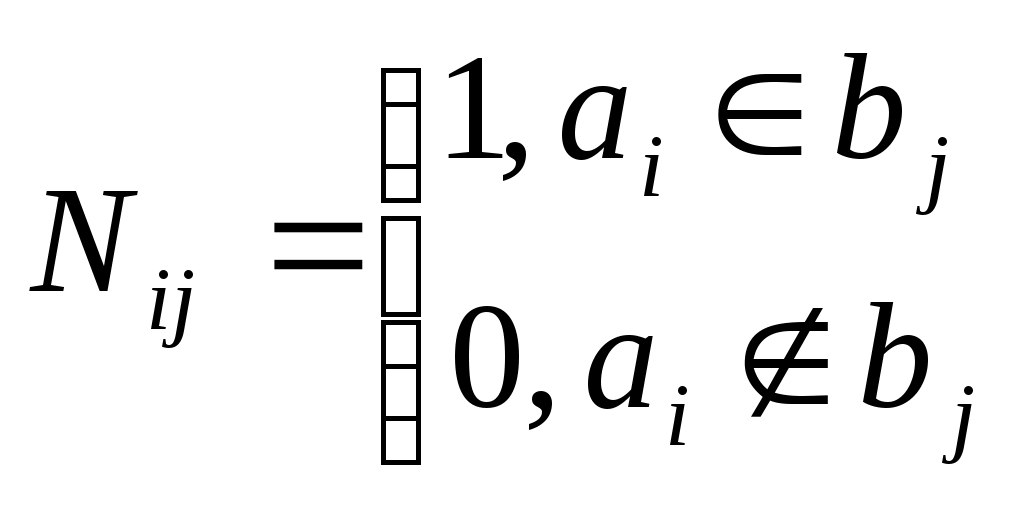 Такая матрица наз-ся матрицей инциденций графа. Дан.матрица зависит от того, как занумерованы ребра. Если в графе все вершины имеют степень 0, то матрицы инциденций не сущ-ет.18. Опред-е графа. Матрицы смежностей и инциденций. Методы хранения графов в памяти ЭВМ. Графом назыв-ся пара множ-в Г=[А,В], где А – любое непустое множ-во, а В – множ-во, кот-е явл-ся подмножеством множ-ва V(A). Матрицей смежности M порядка n назыв-ся матрица, сост-я из чисел mij, равных сумме чисел ориентиров-х ребер, идущих из аi в аj (или чисел неориентированных ребер, соединяющих эти вершины) 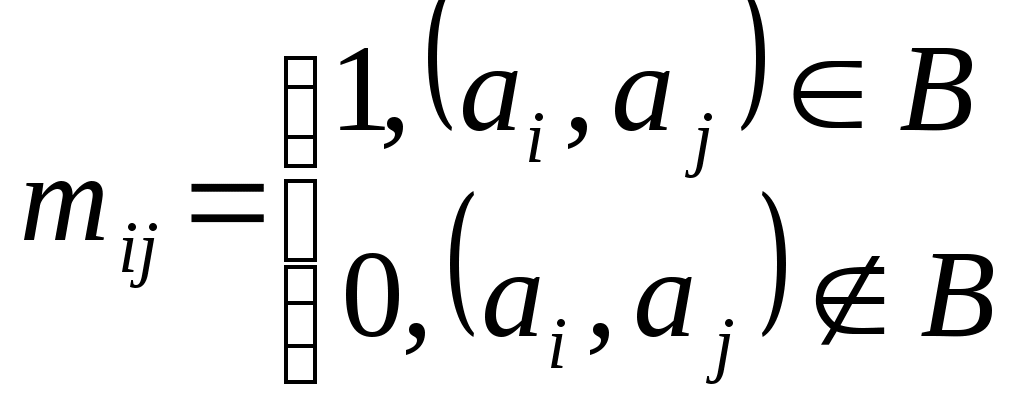 Эта матрица симметричная. #. b1 = (1,2); b2 = (1,3); b3 = (1,4); b4 = (1,5); b5 = (2,3); b6 = (3,4).
Другой вариант матричного представления — матрица инциденций является классическим способом в теории графов. Это не экономичный способ задания. 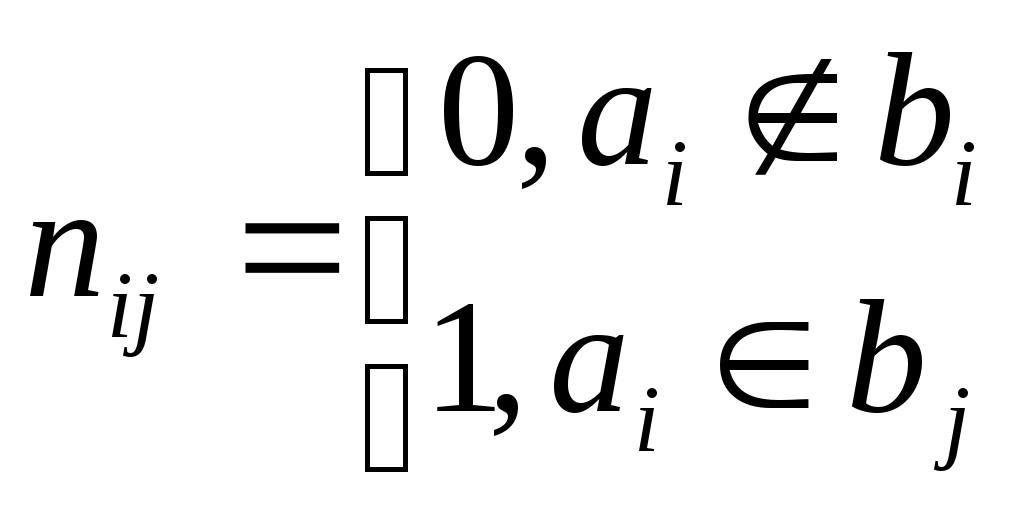  Данная матрица зависит от того как занумерованы ребра. #. b1 = (1,2); b2 = (1,3); b3 = (1,4); b4 = (1,5); b5 = (2,3); b6 = (3,4). i=5; j=6.
В данной матрицы в каждом столбце две 1, т.к. одному ребру всегда инцидентно только две вершины. Если в графе все вершины имеют степень 0, то матрица инцидентности не сущ-ет. В ЭВМ удобно представлять графы в виде матриц смежнотей: если направление ребра противоположено, то в матрицу составим (-1). 19. Путь в графе и связные комп-ты графа. Цепи, простые цепи, циклы, простые циклы. Операции удал-я вершины, уд-я ребра. Дерево и его особ-ти. Графом называется пара множеств Г=[А,В], где А – любое непустое множество, а В – множество, которое является подмножеством множества V(A). Элементы из А называются вершинами графа, а элементы из В – его ребрами. Например, А={1,2,3,4,5}, В={(1,2),(2,3),(3,4),(1,5),(1,4),(3,1)}. Неупорядоченная пара вершин – ребро, а упорядоченная пара – дуга. Путем в графе Г называется такая последовательность дуг, в которой конец каждой последующей дуги совпадает с началом предыдущей. Длиной пути называют число входящих в этот путь дуг. Путь может быть конечным и бесконечным. Путь, в котором никакая дуга не встречается дважды, называется элементарным. Подграф содержит подмножество вершин графа и все соединяющие их рёбра. Компонента связности – максимально связанный подграф. Путь без повтор-ся ребер наз-ся цепью, а цепь без повтор-ся вершин называется простой. Цепь, в кот-й совпадают концевые вершины наз-ся циклом, а цикл, в кто-м нет повто-х вершин, кроме концевых, наз-ся простым. Граф, содержащий только ребра, называется неориентированным; граф, содержащий только дуги – ориентированным или орграфом. Граф называется петлей, если его начало и конец совпадают. Удаление ребра. Г=[А,В] и a А, b В. Удалить ребро b это значит построить новый граф Г`=[А` ,В`], в кот-м А`=А, В`=В\b      Удаление вершин. Г=[А,В] и a А, чтобы удалить вершину а из Г=[А,В] нужно, построить граф новый Г`=[А` ,В`], в кот-м А`=А\{a}, В` получится из В удал-е все ребра. (а будет на пересечении) Д   ерево – это граф без циклов. Граф называется связным, если для любых двух вершин существует путь, соединяющий эти вершины. (первый явл., а второй не явл.). Если Г=[А,В] явл. Деревом и число его вершин = р, то о числе ребер можно сказать совершенно опред-но: в дереве имеется еще одна особенность любые две вершины в дереве связаны и при этом единственной простой цепью.29. Сети и потоки в сетях. Задача о максимальном потоке и алгоритм Форда–Фалкерсона. Пусть  - некоторый орграф и f: B→R – вещ-но-значная f-я на мн-ве ребер, тогда пара  наз-ся сетью, а f-я f наз-ся f-цией пропускной способ-ти сети. Если f-я g: B→R удовлетворяет нерав-ву: gf, то g наз-ся потоком в сети. Пусть L: B→R – любая f-я и U, VА, символ h(U,V) будет обозначать сумму знач-й f-и h на ребрах (х,у)В, таких что хU, yV. Если U состоит из одной вершины a, то h(a,V) обозначает сумму весов ребер, начин-щихся в U и заканч-щихся в вершинах из V, аналогично h(U,a) – сумма знач-й f-и h на ребрах, начин.в U и заканч.в вершине а. Поток g: B→R в сети  ,f наз-ся стационарным, если 2вершины U, VA и число WR такие, что выполн-ся след.усл-я: 1)g(U,A)-g(A,U)=W. 2)g(V,A)-g(A,V)=-W. 3)g(x,A)-g(A,x)=0 (д/любых хА, но U и V. Известна след.классич.задача о max потоке: в дан.сети д/дан.источника и д/дан.стока найти стац.поток max-возможной величины. Можно док-ть, что дан.задача всегда имеет реш-е. Д/реш-я этой задачи сущ-ет много различ.алг-мов, одним из ктр явл-ся алг-м Форда-Фалкерсона. Постановка задачи: Д/опр-я max потока от некоторой вершины S графа (источника) к нектр вершине t графа (сток) использ-ся много различ.алг-мов. При этом кажд.дуге (орграф) (i,j) приписана нектр пропуск.способ-ть с(i,j), опр-щая max знач-е потока, ктр может протекать по дан.дуге. Алг-м Ф-Ф основан на «технике меток». Введем опр-я: разрезом наз-ся мн-во дуг, удаление ктр из сети приводит к разрыву всех путей, ведущих из S в t. Пропуск.способ-ть разреза – Сум.пропуск.способ-ть дуг его составляющих. Разрез с min пропуск.способ-тью наз-ся min разрезом. Т.Ф-Ф: величина кажд.потока из S в t не превосходит пропуск.способ-ти min разреза, разделяющего S и t, причем сущ-ет поток, достигающий этого знач-я. Если поток min, то по Т.Ф-Ф max поток не будет превышать 4ед-цы. Найти max поток, т.е. его распред-е по дугам, можно опр-ть методом перебора. Удачный выбор данных позволяет сделать программ.код компактным, но очевидно, что этот метод прим-м только д/небольших сетей. Техника меток Ф-Ф заключ-ся в послед-ном (итерацион.) построении max потока путем поиска на кажд.шаге увелич-щейся цепи, т.е. пути послед-ти д/потоков, по ктр можно увеличить. При этом узлы (вершины графа) спец.образом помеч-ся. |