Работа готовая. По степени и характеру воздействия различают влияния опасные и мешающие

• Название: По степени и характеру воздействия различают влияния опасные и мешающие
• Дата: 05.05.2022
• Размер: 0.69 Mb.
• Имя файла: Работа готовая.docx
• Тип: Реферат; #513967
• страница: 5 из 5

зависит от знаков и . При состоянии гармоник на общем графике необходимо учитывать, что масштаб по оси абсцисс для - гармоники должен быть взят в раз большим, чем для первой гармоники.

Так, например, если некоторый отрезок по оси абсцисс для первой гармоники выражает собой угол , то тот же отрезок для третьей гармоники выражает собой угол, в 3 раза больший, т.е. .

На рис. 5 изображены гармоники полученного ряда, а также результирующая (суммарная) кривая:



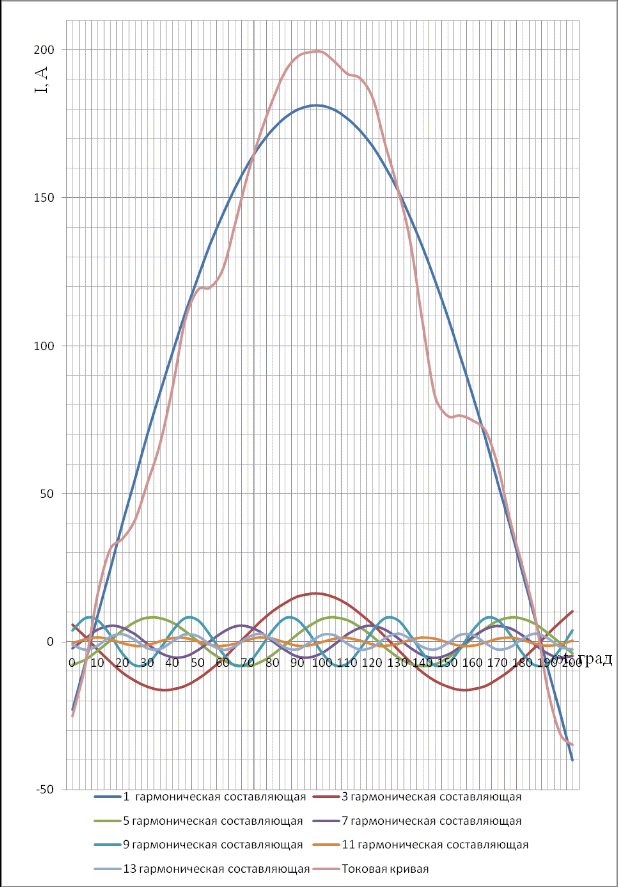
Рисунок 5 - Гармоники ряда

Согласно «Правилам защиты устройств проводной связи проводного вещания от влияния тяговой сети электрических железных дорог переменного тока» величина напряжения шума а двухпроводных телефонных цепях может быть вычислена по формуле:
(16)
Применительно к настоящему курсовой работы величину мешающего напряжения следует вычислять по формуле:
(17)
Величину мешающего напряжения в мВ для k-й гармоники в телефонных цепях тональной частоты вычисляют по формуле:
(18)
Отдельные величины, входящие в эту формулу:

- угловая частота k-й гармонической составляющей, рад/с;

- взаимная индуктивность между контактным проводом и проводом связи для k -й гармонической составляющей, Гн/км.

- ток k-й гармонической составляющей в тяговой сети;

- коэффициент акустического воздействия для k-й гармонической составляющей влияющего тока;

- коэффициент чувствительности двухпроводной цепи для k -й гармонической составляющей влияющего тока;

- результирующий коэффициент экранирующего действия для k -й гармонической составляющей:
, (19)
где - коэффициент экранирования рельсов. Значения этого коэффициента приведены выше;

- коэффициент экранирующего действия оболочки кабеля для k-й гармонической составляющей. Значения его приведены в табл. 6;

- коэффициент, характеризующий волновые процессы в линии связи для k-й гармонической составляющей. При этом:
, (20)
где - постоянная распространения однопроводной цепи, подверженной влиянию для k-й гармонической составляющей. Величина  характеризует изменение амплитуды напряжения вдоль линии, а  - изменение фазового угла. Определение гиперболического синуса от комплексного аргумента может быть произведено по номограммам, приведенным в /1/, либо по формуле:
(21)
Расчетные длины - см. рис. 3.

Если пренебречь возможными резонансными явлениями в тяговой сети, то токи отдельных гармонических составляющих можно принять равными гармоническим составляющим тока электровоза и определить по заданной кривой любым известным графоаналитическим методом.

Один из простейших таких методов (численное интегрирование) состоит в замене интегралов, определяющих синусную и косинусную составляющие (вторая форма ряда Фурье) соответствующими суммами /4/. Взаимное расположение отдельных гармоник относительно друг друга при расчете напряжения шума значения не имеет, а величина k-й гармонической в кривой тока будет равна:
(22)
если и брать в амперах.
Таблица 8 - Значения основных величин (для воздушных линий)

№ гарм	1	3	5	7	9	11	13	15	17	19	21	23
M, 10-4	3,43	2,39	1,94	1,66	1,47	1,32	1,19	1,09	1,02	0,95	0,89	0,83
Iк	128,27	11,55	5,84	3,84	5,87	1	1,93	1,15	0,89	0,33	1,27	0,58
νк	0,86	0,86	0,87	0,88	0,89	0,89	0,91	0,93	0,94	0,96	0,97	0,99
Uш	3,65	3,87	15,47	28,41	83,5	22,13	57,7	45,91	42,44	18,89	86,13	38,51

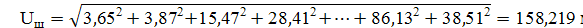
Полученное значение мешающего напряжения не удовлетворяет нормативному значению, поэтому производим аналогичный расчёт для кабельных цепей. рога магнитный электрический

Таблица 9 - Значения основных величин (для кабельных линий)

№ гарм	1	3	5	7	9	11	13	15	17	19	21	23
M,· 10-4	3,43	2,39	1,94	1,66	1,47	1,32	1,19	1,09	1,02	0,95	0,89	0,83
Iк	128,27	11,55	5,84	3,84	5,87	1	1,93	1,15	0,89	0,33	1,27	0,58
νк	0,86	0,86	0,87	0,88	0,89	0,89	0,91	0,93	0,94	0,96	0,97	0,99
Sк	0,0625	0,03	0,02	0,015	0,012	0,01	0,0085	0,0075	0,0065	0,005	0,0045	0,003
Uш	0,007	0,007	0,035	0,072	0,194	0,047	0,111	0,083	0,069	0,024	0,1	0,029

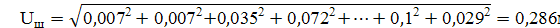
Так как опасное напряжение превышает 36 В, следовательно необходимо увеличить ширину сближения а.










Библиографический список
1. Окладов, С.А. Электромагнитная совместимость на электрических железных дорогах: Методические указания к выполнению курсовой работы для студентов специальности 190401 «Электроснабжение железных дорог» очной и заочной форм обучения/ С.А. Окладов, Е.В. Добрынин. - Самара.: СамГУПС, 2009. - 18 с.

2. Бадер, М.П. Электромагнитная совместимость / М.П. Бадер. - М. : УМК МПС, 2002.

3.Справочник по электроснабжению железных дорог. Т. 1. Под редакцией. К. Г. Марквардта. М.. «Транспорт», 1980, 256 с.

4.Правила защиты устройств проводной связи и проводного вещания от влияния тяговой сети электрических железных дорог, переменного тока. М., «Транспорт», 1973, с. 94.;