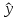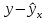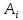Построение линейной парной регрессии. Построение модели парной регрессии. По территориям Центрального района известны данные за 1995 г
 Скачать 74.84 Kb.
|
|
Задание 1 По территориям Центрального района известны данные за 1995 г.: Таблица 1. Исходные данные
1. Рассчитать параметры парной линейной регрессии. 2. Оценить тесноту связи с помощью показателей корреляции и детерминации. 3. С помощью средних коэффициентов эластичности дать сравнительную оценку силы связи фактора с результатом. 4. Оценить с помощью средней ошибки аппроксимации качество уравнений. 5. С помощью F-критерия Фишера оценить статистическую надежность результатов регрессионного моделирования. 6. Рассчитать прогнозное значение результата, если прогнозное значение фактора увеличится на 10% от его среднего уровня. Определить доверительный интервал прогноза для уровня значимости α = 0,05. Решение. 1. Для расчета параметров а и b линейной регрессии у = а + bх решим систему нормальных уравнений относительно а и b: 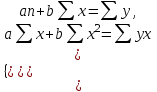 По исходным данным рассчитаем значение всех сумм (таблица 2): Таблица 2. Расчетная таблица
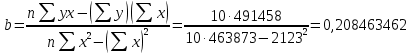 Среднее значение переменных определим по формуле: 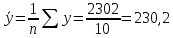 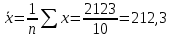 С помощью полученных средних значений переменных определим параметр а: 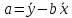 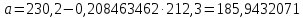 Запишем полученное уравнение парной линейной регрессии: 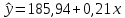 При увеличении прожиточного минимума на 1 тыс.руб. средний размер назначенных пенсий увеличится в среднем на 0,21 процентных пункта. 2. Линейный коэффициент парной корреляции. Для определения линейного коэффициента парной корреляции используем формулу: 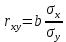 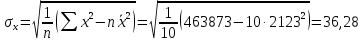 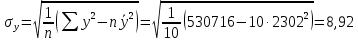 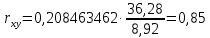 Полученное значение линейного коэффициента парной корреляции говорит о высокой и прямой связи. Коэффициент детерминации равен квадрату коэффициента корреляции: 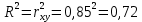 Коэффициент детерминации 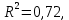 это значит, что вариация результата на 72% объясняется вариацией фактора х.3. Подставив в уравнение регрессии фактические значения х, определим теоретические (расчетные) значения 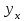 (колонка 7, таблица 2), а также разности между измеренными значениями и рассчитанными (колонка 8, таблица 2). Величины ошибок аппроксимации в колонке 9 (таблица 2) вычислим как абсолютную величину значений в колонке 8 (таблица 2) по отношению к измеренным значениям в колонке 2 (таблица 2) в процентах: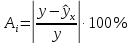 Вычислим величину средней ошибки аппроксимации: 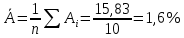 В среднем расчетные значения отклоняются от фактических на 1,6%, что свидетельствует о хорошо подобранной модели уравнения. 4. Вычислим средний коэффициент эластичности линейной регрессии: 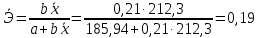 В среднем при увеличении х на 1% значение у увеличивается на 0.19% 5. Вычислим значение F-критерия: 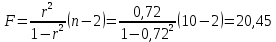 Так как 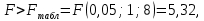 гипотеза Но о случайной природе выявленной зависимости и статистической незначимости параметров уравнения отклоняется. При этом принимается H1, уравнение регрессии признают статистически значимым.6. Далее вычислим прогнозное значение 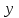 по линейной модели при прогнозном значении фактора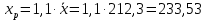 В результате получим прогнозное значение результата: 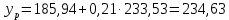 Вычислим доверительный интервал для этого прогноза. Для этого рассчитаем стандартную ошибку прогноза по формуле: 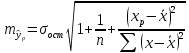 Здесь: 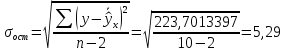 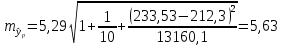 Доверительный интервал рассчитаем по формуле: 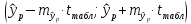 Здесь: 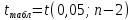 n (берем двухстороннее значение t-критерия Стьюдента): t(0,05;8) = 2,3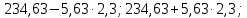 Доверительный интервал равен: 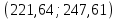 Истинное значение прогноза с вероятностью 0,95 попадает в этот интервал. Задание 2 Имеются следующие данные о продаже объектов недвижимости города (таблица 3): Таблица 3. Исходные данные
Требуется: 1. Построить линейное уравнение множественной регрессии и пояснить экономический смысл его параметров. 2. Рассчитать средние частные коэффициенты эластичности. 3. Определить стандартизированные коэффициенты регрессии. 4. На основе полученных результатов сделать вывод о силе связи результата с каждым из факторов. 5. Определить парные и частные коэффициенты корреляции, а также множественный коэффициент корреляции; сделать выводы. 6. Дать оценку полученного уравнения на основе коэффициента детерминации и общего F-критерия Фишера. |
